21
2
Background
A binary tree is a rooted tree whose every node has at most two children.
A labelled binary tree is a binary tree whose every node is labelled with a positive integer; moreover, all labels are distinct.
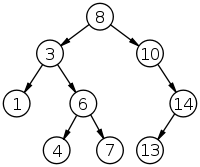
A BST (binary search tree) is a labelled binary tree in which the label of each node is greater than the labels of all the nodes in its left subtree, and smaller than the labels of all the nodes in its right subtree. For instance, the following is a BST:
The pre-order traversal of a labelled binary tree is defined by the following pseudo-code.
function preorder(node)
if node is null then
return
else
print(node.label)
preorder(node.left)
preorder(node.right)
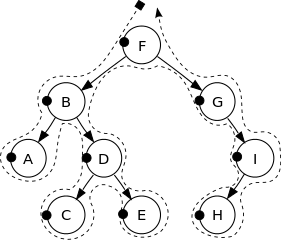
See the following image to get a better intuition:
The vertices of this binary tree are printed in the following order:
F, B, A, D, C, E, G, I, H
You can read more about BSTs here, and more about pre-order traversal here.
Challenge
Given a list of integers \$a\$, your task is to determine whether there is a BST whose pre-order traversal prints exactly \$a\$.
Input
- A non-empty list of distinct positive integers \$a\$.
- Optionally, the length of \$a\$.
Output
- A truthy value if \$a\$ is the pre-order traversal of some BST.
- A falsey value otherwise.
Rules
- Standard rules for valid submissions, I/O, loopholes apply.
- This is code-golf, so shortest solution (in bytes) wins. As usual, don't let ridiculously short solutions in golfy languages discourage you from posting a longer answer in your language of choice.
- This is not a rule, but your answer will be better received if it includes a link to test the solution and an explanation of how it works.
Examples
Input ----> Output
[1] ----> True
[1,2,3,4] ----> True
[5,1,4,2,3] ----> True
[5,4,3,2,1,6,7,8,9] ----> True
[4,2,1,3,6,5,7] ----> True
[8,3,1,6,4,7,10,14,13] ----> True
[2,3,1] ----> False
[6,3,2,4,5,1,8,7,9] ----> False
[1,2,3,4,5,7,8,6] ----> False
[3,1,4,2] ----> False
Check out this link (courtesy of Kevin Cruijssen) to have a visual look at the examples.
1Here a pastebin of the test cases to have a more visual look as to how they are truthy/falsey. Nice challenge btw, +1 from me. – Kevin Cruijssen – 2018-10-19T08:21:11.287
May we assume all integers are positive? – G B – 2018-10-19T10:46:14.107
@GB Yes. I will edit the post now. – Delfad0r – 2018-10-19T11:01:12.603