7
1
Write a program that converts a decimal to a mixed, simplified fraction.
Sample input:
5.2
Sample output:
5 + (1/5)
The code with the shortest length in bytes wins.
7
1
Write a program that converts a decimal to a mixed, simplified fraction.
Sample input:
5.2
Sample output:
5 + (1/5)
The code with the shortest length in bytes wins.
4
y=gets.to_r;puts"#{y.to_i} + (#{y-y.to_i})"
Pretty straightforward.
Interesting solution. I'm honestly surprised you can make such short program with correct output format. – Konrad Borowski – 2014-01-03T17:47:29.133
Ruby has a lot of Lispy features and the Rational class is probably one of the lesser-known ones. However, if the input is a float you're liable to get something like "2 + (1499999999999999/5000000000000000)" – Ibrahim Tencer – 2014-01-04T04:01:20.947
2
'.'/~'+'\.~.@,10\?.@{.@\%.}do;:d/\d/'/'@
Requires no line terminator in the input. Can probably be golfed further.
1
Executed from a TI-84 calculator
i`A:floor(A)→B:A-B→A:d`Bd`A►Frac
1
No cigar this time. Numerator, Denominator and Rationalize are big words.
f@x_:=(Row@{⌊#⌋,"+",Numerator@#~Mod~(d=Denominator@#)/d})&[Rationalize@x]
Example
f[23.872]
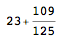
1
`A:floor(A)→B:A-B→A~B~A►Frac
The source code for your compiler cannot be run since iX2Web is not available. The link in your site is bad as well. – mbomb007 – 2015-04-13T20:58:54.103
1
OK, this isn't the shortest. But the proper way to convert decimals to fractions is to use continued fractions.
#include <stdio.h>
#include <string.h>
#include <math.h>
int main(int argc, char **argv) {
double f = 152/147.;
int temp, i, cf[50], n=0, d=1;
double prec = 1e-6;
memset(cf,0,sizeof(memset));
for (i=0;i<50 && prec<1;i++) {
cf[i] = f;
/* Next line assumes division by zero evaluates to inf */
f = 1/(f-cf[i]);
prec*=f;
}
for (;i>=0;i--) {
temp = n;
n = n*cf[i] + d;
d = temp;
}
if (cf[0] == 0)
printf("%d/%d\n",d,n);
else
printf("%d %d/%d\n",cf[0],d,n);
}
1
from fractions import*
a,b=input().split(".")
print("%s + (%s)"%(a,Fraction("."+b)))
Doesn't return the output in correct format. + should be returned (but otherwise, it's close to expected format). – Konrad Borowski – 2014-01-03T07:03:05.233
@GlitchMr Edited the format. – Wasi – 2014-01-03T07:52:42.987
Also, there are parens. Dunno why, but the OP put them. – Konrad Borowski – 2014-01-03T12:42:54.753
@GlitchMr Added those creepy parens. Now the code size raised to 84 :-( – Wasi – 2014-01-03T12:58:09.197
1
Does the output in right, expected format. Would be way shorter if output in invalid format would be allowed. This gets a number, converts it to rational. nude method returns denominator and numerator (there are separate denominator and numerator methods, but they are crazily long.
[] is a reduce operator which takes operator between square brackets, and in this case, I use it to shorten the code (so I wouldn't have to specify both array elements, because they are already in correct order (but if they wouldn't, there are R operators (like R/, R%, Rdiv, and Rmod) that reverse the order of arguments for operator)). {} in double quotes puts the result of code in string (like #{} in Ruby).
my \ is declaration of sigilless variable. In this case it doesn't save characters, but it doesn't waste them either, so why not use it. I could have used my@, and it would use identical number of characters.
my \n=get.Rat.nude;say "{[div] n} + ({[%] n}/{n[1]})"
Sample output (just to show the correct format):
~ $ perl6 -e 'my \n=get.Rat.nude;say "{[div] n} + ({[%] n}/{n[1]})"'
42.42
42 + (21/50)
If negative number support is needed, this would work (2 bytes more).
~ $ perl6 -e 'my \n=get.Rat.nude;say "{[div] n} + ({[mod] n}/{n[1]})"'
-42.42
-42 + (-21/50)
1
How about the way they tought us at grammar school?
f=function(s){
gcd=function(a,b)if(!b)a else gcd(b,a%%b)
a=strsplit(s,'\\.')[[1]]
p=10^nchar(a[2])
x=strtoi(a[2])
d=gcd(x,p);
cat(a[1]," + (",x/d,"/",p/d,")",sep="");
}
Vaguely: works for positive decimals with finite decimal fraction.
> f("23.872")
23 + (109/125)
Input must be a string matching "[0-9]+\.[0-9]+" regular expression.
1
Isn't pretty, but whatever
import Data.Ratio
main=let r '%'='/';r c=c in interact$(\(x,y)->show x++" + "++map r(show$approxRational y 1e-9)).properFraction.read
0
kind of cheating, but pressing these characters in a mathematica notebook looks it up in wolfram alpha, which gives the mixed fraction form among other information
==5.2
==1.234
etc...
5Easy:
1.2345 = 12345/10000. You give me the precision & I'll give you the fraction! – recursion.ninja – 2014-01-02T21:52:07.913Do you mean simplified fractions? – hkk – 2014-01-02T21:53:04.673
i meant mixed fractions – belvi – 2014-01-02T21:58:15.503
basically: find how many spaces the decimal goes beyond the decimal point (e.g. 2.357 is 3 digits after decimal), then turn it into improper, unsimplified: 2357/1000 and then, have a list of primes, starting at lowest, try to divide both numbers by it without remainder, then try it on that until at least one of the numbers is a prime and the other is not divisible by that number, and you're done – markasoftware – 2014-01-02T22:04:17.200
@CrowdStar: Does the fractional part need to be simplified? – Gelatin – 2014-01-02T22:09:43.633
Yep, it has to be. @Gelatin – belvi – 2014-01-02T22:11:49.520
25.2 != 5+1/2... – Kevin – 2014-01-02T22:28:46.643
@Markasoftware: That won't necessarily work (the factor might not be prime) and it could take a long time. The best way (AFAIK) is to find the gcd of both (using the Euclidean algorithm) and divide through. – Gelatin – 2014-01-02T22:36:11.593
Is there a convention for negative mixed fractions? What about proper fractions?: 0+3/7 or simply 3/7 ? – DavidC – 2014-01-02T23:44:34.400
@Gelatin I'm pretty sure all whole numbers which are greater than 1 and are not prime have at least one factor that is prime. – markasoftware – 2014-01-03T17:16:13.497
@Markasoftware: I guess it would work if you did it more than once. – Gelatin – 2014-01-03T17:22:52.657