When in Rome, Count as Romans do?

Question

Background

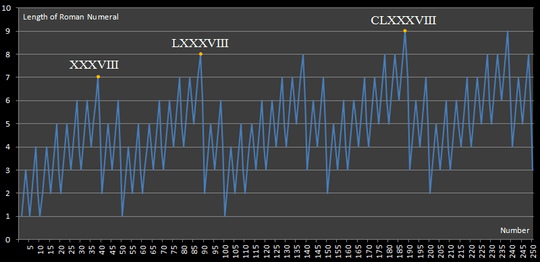
This challenge is inspired by this website, which published the following diagram:

This diagram shows us that the longest Roman Numeral expression under 250 is that of 188, which requires 9 numerals to express.

Challenge

The standard symbols used to express most Roman Numerals are the following: {I, V, X, L, C, D, M}, where the characters' numeric values are M=1000, D=500, C=100, L=50, X=10, V=5, I=1.

In this challenge, your goal is to, given an positive integer n, compute the number of valid Roman Numeral representations that can be composed through concatenating n of the standard symbols.

Then, your program must output the result of this computation!

Input: A positive integer n.

Output: The number of valid roman numeral expressions of length n.

Rules for Roman Numeral Expressions

Roman Numerals originally only had "additive" pairing, meaning that numerals were always written in descending order, and the sum of the values of all the numerals was the value of the number.

Later on, subtractive pairing, the use of placing a smaller numeral in front of a larger in order to subtract the smaller from the larger, became commonplace to shorten Roman Numeral expressions. Subtractive pairs cannot be chained, like in the following invalid expression: IXL.

The following are the modern day rules for additive and subtractive pairing.

1. Only one I, X, and C can be used as the leading numeral in part of a subtractive pair.
2. I can only be placed before V or X in a subtractive pair.
3. X can only be placed before L or C in a subtractive pair.
4. C can only be placed before D or M in a subtractive pair.
5. Other than subtractive pairs, numerals must be in descending order (meaning that if you drop the leading numeral of each subtractive pair, then the numerals will be in descending order).
6. M, C, and X cannot be equalled or exceeded by smaller denominations.
7. D, L, and V can each only appear once.
8. Only M can be repeated 4 or more times.

Further Notes

• We will not be using the bar notation; rather, we will simply add more Ms to express any number.

• These are the only rules that we will follow for our roman numerals. That means that odd expressions, such as IVI, will also be considered valid in our system.

• Also remember that we are not counting the number of numbers that have expressions of length n, since some numbers have multiple expressions. Instead, we are solely counting the number of valid expressions.

Test Cases

1 → 7

2 → 31

3 → 105

I checked the above by hand, so please make sure to double check the test cases, and add more if you can!

Winning Criteria

This is a code-golf challenge, so have fun! I will only accept solutions that can handle at least inputs from 1 through 9. Any more is bonus!

Edit

As requested by commenters, find below, or at this pastebin link, the 105 combos I counted for n=3

III IVI IXI IXV IXX VII XII XIV XIX XVI XXI XXV XXX XLI XLV XLX XCI XCV XCX XCL XCC LII LIV LIX LVI LXI LXV LXX CII CIV CIX CVI CXI CXV CXX CXL CXC CLI CLV CLX CCI CCV CCX CCL CCC CDI CDV CDX CDL CDC CMI CMV CMX CML CMC CMD CMM DII DIV DIX DVI DXI DXV DXX DXL DXC DLI DLV DLX DCI DCV DCX DCL DCC MII MIV MIX MVI MXI MXV MXX MXL MXC MLI MLV MLX MCI MCV MCX MCL MCC MCD MCM MDI MDV MDX MDL MDC MMI MMV MMX MML MMC MMD MMM

Edit 2:

Use the following non-golfed code, as courtesy of Jonathan Allan to check your results.

Edit 3:

I apologize for all of the errors in this challenge. I'll make sure to do a better job next time!

Answer 1

Retina, 111 bytes

~(`.+
*$(CM)CDXCXCXCXLIXIXIXIVII
.(.)
.+¶$$&$¶$$&$1$¶$$&$&¶L`.{0,$+}\b¶D`¶
¶$
¶.+¶$$&$¶$$&I¶L`[A-Z]{$+}\b¶D`¶.+

Try it online! This is a complete rewrite as I misunderstood rule 1. to mean that you could only use one each of subtractive I, X and C. Explanation: The first part of the script expands the input into a string of CM pairs followed by the other possible subtractive pairs. Each pair is optional, and the first character of each pair is also optional within the pair. The third stage then expands the list of pairs into a list of Retina commands that take the input and create three copies with the option of the second or both characters from the pair, then trims and deduplicates the results. The final stage then appends code to perform the final tasks: first to expand the input to possibly add a final I, then to filter out results of the wrong length, then to deduplicate the results, and finally to count the results. The resulting Retina script is then evaluated.

Note: In theory 15 bytes could be saved from the end of the 4th line but this makes the script too slow to demonstrate on TIO even for n=1.

Answer 2

Python 2, 177 168 162 bytes

import re,itertools as q
f=lambda n:sum(None!=re.match("^M*(CM|CD|D?C{0,3})(XC|XL|L?X{0,3})(IX|IV|V?I{0,3})$",(''.join(m)))for m in q.product('MDCLXVI',repeat=n))

Try it online!

I'm pretty new, help me golf this! This checks for actual roman numerals, the regex needs to be adjusted to account for the odd cases such as IVI

-9 bytes thanks to @Dead Possum!

-6 bytes thanks to @ovs

Answer 3

JavaScript (ES7), 133 bytes

Edit: Fixed to match the results returned by Jonathan Allan's code, which was given as a reference implementation by the OP.

---

n=>[...Array(m=k=7**n)].reduce(s=>s+/^1*5?4{0,3}3?2{0,3}6?0{0,3}$/.test((--k+m).toString(7).replace(/0[62]|2[34]|4[51]/g,s=>s[1])),0)

Try it online!

How?

1) We generate all numbers of \$N\$ digits in base 7 with an extra leading \$1\$:

[...Array(m = k = 7 ** n)].reduce(s => … (--k + m).toString(7) …, 0)

From now on, each digit will be interpreted as a Roman numeral symbol:

$$\begin{array}{}0\longleftrightarrow \text{I}, & 1\longleftrightarrow \text{M}, & 2\longleftrightarrow \text{X}, & 3\longleftrightarrow \text{L},\\ 4\longleftrightarrow \text{C}, & 5\longleftrightarrow \text{D}, & 6\longleftrightarrow \text{V} \end{array}$$

2) We replace all valid subtractive pairs of the form AB with B:

.replace(/0[62]|2[34]|4[51]/g, s => s[1]))  // in the code
.replace(/I[VX]|X[LC]|C[DM]/g, s => s[1]))  // with Roman symbols

Examples:

• XLIXIV becomes LXV
• XIIV becomes XIV, leaving a I that will make the next test fail
• IC remains unchanged, which also leaves an invalid I in place

3) We check that the remaining symbols are in the correct order and do not appear more times than they're allowed to:

/^1*5?4{0,3}3?2{0,3}6?0{0,3}$/.test(…)  // in the code
/^M*D?C{0,3}L?X{0,3}V?I{0,3}$/.test(…)  // with Roman symbols

Answer 4

C, 150 123 bytes

I didn't read the description closely enough, so this produces the number of standard Roman numerals (where expressions like IVI aren't counted). Since I put some effort into it, I thought I would share anyway.

#define F(X) for(X=10;X--;)
x[]={0,1,2,3,2,1,2,3,4,2};f(i,o,a,b,c){for(i++;i--;)F(a)F(b)F(c)o+=i==x[a]+x[b]+x[c];return o;}

Original (150 bytes):

#define F(X) for(X=10;X--;)
i,o,a,b,c,x[]={0,1,2,3,2,1,2,3,4,2};main(){scanf("%i",&i);for(i++;i--;)F(a)F(b)F(c)o+=i==x[a]+x[b]+x[c];printf("%i\n",o);}