Nonogram line brute-force solving

Question

Background

Nonogram, also known as Picross or Griddlers, is a puzzle where the objective is to determine if each cell on the 2D grid should be colored or left blank, using the numbers of consecutive colored cells on each line.

The following is an example Nonogram puzzle with solution.

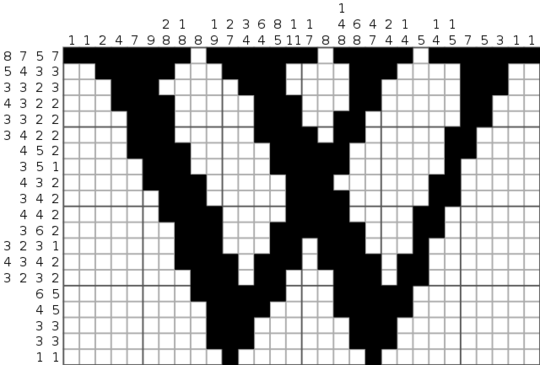
The problem is, some commercial Nonogram games/mobile apps have puzzles which are not solvable by hand (e.g. have multiple solutions, or require deep backtracking). However, they also offer some lives to the player, where one life is lost when you try to color a cell whose correct answer is blank. So now it's time to brute-force those nasty "puzzles"!

In order to simplify the task, imagine just one line with its clue and nothing else:

3 7 | _ _ _ _ _  _ _ _ _ _  _ _ _ _ _

The [3,7] are the clues, and the line length is 15 cells. Since it has multiple possible solutions, we need to risk some lives in order to fully solve this line (i.e. determine all colored cells).

Challenge

Given a line with clues (a list of positive integers) and the line length, find the maximum number of lives you will lose, assuming that you brute-force the line with optimal strategy.

Note that you always guess colored cells. In actual games, guessing empty cells (either right or wrong) have no effect on your lives, so you can't "solve" the puzzle that way.

Also, you can assume the input always represents a valid Nonogram line, so you don't need to worry about something like [6], 5.

Explanation

Let's look at some simpler examples first.

[1,2], 5

There are exactly three possibilities for this line (O is a colored cell, . is an empty one):

O . O O .
O . . O O
. O . O O

If we try coloring cell 0 (0-based index from left), one of the following happens:

• The cell is correctly colored. Now we have two possibilities, and we can choose between cell 2 and cell 4 in order to fully solve the line. Either case, we will lose one life in the worst case.
• The cell is empty, and we lose a life. In this case, we have already identified the unique solution to this line, so we're done with 1 life lost.

Therefore, the answer for [1,2], 5 is 1.

[5], 10

Binary search? Nope.

The most obvious first choice is 4 or 5, which will reveal one possibility if it's blank (at a cost of 1 life). Let's say we chose 4 first. If cell 4 is indeed colored, we extend it to the left, i.e. try 3, 2, 1 and 0 until a life is lost (or cell 0 is colored, then we end up spending no lives at all). Whenever a life is lost, we can uniquely determine the solution, e.g. if we see something like this:

_ _ X O O _ _ _ _ _

then we already know the answer is this:

. . . O O O O O . .

Therefore, the answer for [5], 10 is also 1.

[3,7], 15

Start with cell 11, which, if empty, will reveal the following solution right away.

O O O . O O O O O O O X . . .

Then try 12, which, if empty, gives two possibilities which can be solved at the cost of 1 extra life.

O O O . . O O O O O O O X . .
. O O O . O O O O O O O X . .

Now try 2. If empty, it leads to three possibilities which can be solved similarly to the [1,2], 5 example.

. . X O O O . O O O O O O O .
. . X O O O . . O O O O O O O
. . X . O O O . O O O O O O O

If you keep minimizing the risk in this manner, you can reach any solution with max. 2 lives spent.

Test Cases

[1,2] 5 => 1
[2] 5 => 2
[1] 5 => 4
[] 5 => 0
[5] 10 => 1
[2,1,5] 10 => 0
[2,4] 10 => 2
[6] 15 => 2
[5] 15 => 2
[4] 15 => 3
[3,7] 15 => 2
[3,4] 15 => 3
[2,2,4] 15 => 4
[1,1,1,1,1,1,1] 15 => 2

[2,1,1,3,1] 15 => 3
[1,1,1,2,1] 15 => 5

For the last two cases, the optimal strategy is not going through the minimum blanks, but simply going from left to right (or right to left). Thanks to @crashoz for pointing it out.

Rules

Standard code-golf rules apply. The shortest valid submission in bytes wins.

Bounty

If someone comes up with a polynomial-time algorithm (with the proof of correctness), I will award +100 bounty to such a solution.

Answer 1

Ruby, 85 bytes

f=->l,n,s=n-l.sum-l.size+1{*a,b=l;b&&s>0?(a[0]?1+f[a,n-b-2,s-1]:(n.to_f/b).ceil-1):0}

Try it online!

Explanation

The first step is to establish a recursive divide and conquer strategy to solve subproblems. I will use the variables \$l=[l_1,l_2,...,l_x]\$ for the list of clues, \$x\$ for the number of clues and \$n\$ for the number of cells.

Try to fit the last clue \$l_x\$:
We test the cell at \$n-l_x\$
(1) If it's empty: then all of the clues are before \$n-l_x\$. So we lose a life and we call recursively \$1+f(l,n-l_x)\$
(2) If it's colored: We are not sure how to place the last clue, so we test every cells to the right until finding an empty one The worst case is finding the empty cell at the last index, we lose a life, but we have placed the last clue so we can call recursively \$1+f(\tilde{l},n-l_x-2)\$ where \$\tilde{l}\$ is \$l\$ without the last clue.

So we can get the number of lives with this function $$ f(l,n)=\begin{cases} 0, & \text{if } \sum_1^xl_i+x-1 \geq n\\ \lceil \frac{n}{l_x} \rceil - 1 & \text{if } x= 1\\ 1+\max\begin{cases} f(l,n-l_x)\\ f(\tilde{l},n-l_x-2) \end{cases}, & \text{otherwise} \end{cases} $$

Here is an example _ are unknown, X is a known space, O is a known colored cell and L is life lost

[2,2,4] 15                  _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
(1) -> [2,2,4] 11           _ _ _ _ _ _ _ _ _ _ _ L X X X
    (1) -> [2,2,4] 7        _ _ _ _ _ _ _ L X X X L X X X
        0                   X X X L X X X L X X X L X X X
    (2) -> [2,2] 5          _ _ _ _ _ X O O O O L L X X X
        0                   O O X O O X O O O O L L X X X 
(2) -> [2,2] 9              _ _ _ _ _ _ _ _ _ X O O O O L
    (1) -> [2,2] 7          _ _ _ _ _ _ _ L X X O O O O L
        (1) -> [2,2] 5      _ _ _ _ _ L X L X X O O O O L
            0               O O X O O L X L X X O O O O L
        (2) -> [2] 3        _ _ _ X O O L L X X O O O O L
            1               O O L X O O L L X X O O O O L               
    (2) -> [2] 5            _ _ _ _ _ X O O L X O O O O L
        2                   O O L L X X O O L X O O O O L

It makes a binary tree, to get the number of lives lost, we just need to count the maximum height of the tree. However this makes it \$\mathcal{O}(2^n)\$ because we evaluate all of the branches. We can do better.

Let's define a cost function \$h\$ that will help us "choose" the right branch at each step.

$$ h(l,n)=n - \sum_1^xl_i-x+1 $$

\$h\$ counts the number of superfuous spaces we have if we pack all the clues with one space in between. So it is essentially an indicator of how much lives we are going to need to solve the instance, the higher it is, the more lives are necessary. The idea is to apply this indicator on our recursive formula.

By definition of \$h\$ we have, $$ \begin{align} h(l,n-l_x) &= n - l_x - \sum_1^xl_i-x+1\\ & =(n - \sum_1^xl_i-x+1) - l_x\\ & = h(l,n) - l_x \end{align} $$

And, $$ \begin{align} h(\tilde{l},n-l_x-2) &= n - l_x - 2 - \sum_1^{x-1}l_i-(x-1)+1\\ & =(n - \sum_1^xl_i-x+1) - 1\\ & = h(l,n) - 1 \end{align} $$

Then, $$ h(l,n)=\begin{cases} \leq 0, & \text{if } \sum_1^xl_i+x-1 \geq n\\ n - l_x, & \text{if } x=1\\ \max\begin{cases} h(l,n-l_x)+l_x\\ h(\tilde{l},n-l_x-2)+1 \end{cases}, & \text{otherwise} \end{cases} $$

We want to maximize \$h\$ at each step to get the worst case so let's check the difference between the two expressions in the recurrence

$$ [h(l,n-l_x)+l_x] - [h(\tilde{l},n-l_x-2)+1]\\ \begin{align} &= n-l_x-n - \sum_1^xl_i-x+1 + l_x - [n-l_x-2 -\sum_1^{x-1}l_i-(x-1)+1+1]\\ &=-2 \end{align} $$

$$ \begin{align} [h(l,n-l_x)+l_x] - [h(\tilde{l},n-l_x-2)+1] &=-2\\ [h(l,n-l_x)+l_x] - [h(\tilde{l},n-l_x-2)+1] &< 0\\ [h(l,n-l_x)+l_x] &< [h(\tilde{l},n-l_x-2)+1] \end{align} $$ So the 2nd expression is always the max, we can remove the first one

$$ h(l,n)=\begin{cases} \leq 0, & \text{if } \sum_1^xl_i+x-1 \geq n\\ n - l_x, & \text{if } x=1\\ h(\tilde{l},n-l_x-2)+1 & \text{otherwise} \end{cases} $$

Finally this recursive definition of \$h\$ shows us that option (2) in function \$f\$ is always the worst case (giving the maximum number of possibilities i.e. maximizing \$h\$)

$$ f(l,n)=\begin{cases} 0, & \text{if } \sum_1^xl_i+x-1 \geq n\\ \lceil \frac{n}{l_x} \rceil - 1 & \text{if } x= 1\\ 1+ f(\tilde{l},n-l_x-2), & \text{otherwise} \end{cases} $$

Every step we decrease \$n\$ by at least 3 and there is now a single recursive call, complexity is \$\mathcal{O}(n)\$

Answer 2

Python, 303 289 bytes

First golf in a long time, so there may be a lot of excess fat. (Thanks Jo King for finding 14 bytes-worth.)

Function f generates all the possible arrangements (though always with a blank as the first character, but that's fine as long as we increment the length by 1 before we call it). Function g picks the position with the fewest number of blanks and recurses. Function h puts them together.

f=lambda l,n:["."*i+"X"*l[0]+c for i in range(1,n-l[0]+1)for c in f(l[1:],n-i-l[0])]if l else["."*n]
def g(q,n):O,X=min([[[p[:i]+p[i+1:]for p in q if p[i]==u]for u in".X"]for i in range(n)],key=lambda x:len(x[0]));return(len(q)>1)*1and max(1+g(O,n-1),g(X,n-1))
h=lambda l,n:g(f(l,n+1),n+1)

The examples all run fine:

>>> h([3,7],15)
2
>>> h([3,4],15)
3
>>> h([1,1,1,2,1],15)
6