Java
I've hidden this bytecode:
public class Functions {
public static int add() {
try {
Thread.sleep(100000);
} catch (InterruptedException ex) {
}
return 0;
}
}
in this file:
import java.lang.reflect.InvocationTargetException;
import java.math.BigInteger;
public class Fac extends ClassLoader {
static final byte[] FunctionsClass = {
(byte)0xCA,(byte)0xFE,(byte)0xBA,(byte)0xBE,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x33,(byte)0x00,(byte)0x20,(byte)0x0A,(byte)0x00,(byte)0x07,(byte)0x00,(byte)0x17,(byte)0x05,
(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x01,(byte)0x86,(byte)0xA0,(byte)0x0A,(byte)0x00,(byte)0x18,(byte)0x00,(byte)0x19,(byte)0x07,(byte)0x00,(byte)0x1A,
(byte)0x07,(byte)0x00,(byte)0x1B,(byte)0x07,(byte)0x00,(byte)0x1C,(byte)0x01,(byte)0x00,(byte)0x06,(byte)0x3C,(byte)0x69,(byte)0x6E,(byte)0x69,(byte)0x74,(byte)0x3E,(byte)0x01,
(byte)0x00,(byte)0x03,(byte)0x28,(byte)0x29,(byte)0x56,(byte)0x01,(byte)0x00,(byte)0x04,(byte)0x43,(byte)0x6F,(byte)0x64,(byte)0x65,(byte)0x01,(byte)0x00,(byte)0x0F,(byte)0x4C,
(byte)0x69,(byte)0x6E,(byte)0x65,(byte)0x4E,(byte)0x75,(byte)0x6D,(byte)0x62,(byte)0x65,(byte)0x72,(byte)0x54,(byte)0x61,(byte)0x62,(byte)0x6C,(byte)0x65,(byte)0x01,(byte)0x00,
(byte)0x12,(byte)0x4C,(byte)0x6F,(byte)0x63,(byte)0x61,(byte)0x6C,(byte)0x56,(byte)0x61,(byte)0x72,(byte)0x69,(byte)0x61,(byte)0x62,(byte)0x6C,(byte)0x65,(byte)0x54,(byte)0x61,
(byte)0x62,(byte)0x6C,(byte)0x65,(byte)0x01,(byte)0x00,(byte)0x04,(byte)0x74,(byte)0x68,(byte)0x69,(byte)0x73,(byte)0x01,(byte)0x00,(byte)0x0B,(byte)0x4C,(byte)0x46,(byte)0x75,
(byte)0x6E,(byte)0x63,(byte)0x74,(byte)0x69,(byte)0x6F,(byte)0x6E,(byte)0x73,(byte)0x3B,(byte)0x01,(byte)0x00,(byte)0x03,(byte)0x61,(byte)0x64,(byte)0x64,(byte)0x01,(byte)0x00,
(byte)0x03,(byte)0x28,(byte)0x29,(byte)0x49,(byte)0x01,(byte)0x00,(byte)0x02,(byte)0x65,(byte)0x78,(byte)0x01,(byte)0x00,(byte)0x20,(byte)0x4C,(byte)0x6A,(byte)0x61,(byte)0x76,
(byte)0x61,(byte)0x2F,(byte)0x6C,(byte)0x61,(byte)0x6E,(byte)0x67,(byte)0x2F,(byte)0x49,(byte)0x6E,(byte)0x74,(byte)0x65,(byte)0x72,(byte)0x72,(byte)0x75,(byte)0x70,(byte)0x74,
(byte)0x65,(byte)0x64,(byte)0x45,(byte)0x78,(byte)0x63,(byte)0x65,(byte)0x70,(byte)0x74,(byte)0x69,(byte)0x6F,(byte)0x6E,(byte)0x3B,(byte)0x01,(byte)0x00,(byte)0x0D,(byte)0x53,
(byte)0x74,(byte)0x61,(byte)0x63,(byte)0x6B,(byte)0x4D,(byte)0x61,(byte)0x70,(byte)0x54,(byte)0x61,(byte)0x62,(byte)0x6C,(byte)0x65,(byte)0x07,(byte)0x00,(byte)0x1A,(byte)0x01,
(byte)0x00,(byte)0x0A,(byte)0x53,(byte)0x6F,(byte)0x75,(byte)0x72,(byte)0x63,(byte)0x65,(byte)0x46,(byte)0x69,(byte)0x6C,(byte)0x65,(byte)0x01,(byte)0x00,(byte)0x0E,(byte)0x46,
(byte)0x75,(byte)0x6E,(byte)0x63,(byte)0x74,(byte)0x69,(byte)0x6F,(byte)0x6E,(byte)0x73,(byte)0x2E,(byte)0x6A,(byte)0x61,(byte)0x76,(byte)0x61,(byte)0x0C,(byte)0x00,(byte)0x08,
(byte)0x00,(byte)0x09,(byte)0x07,(byte)0x00,(byte)0x1D,(byte)0x0C,(byte)0x00,(byte)0x1E,(byte)0x00,(byte)0x1F,(byte)0x01,(byte)0x00,(byte)0x1E,(byte)0x6A,(byte)0x61,(byte)0x76,
(byte)0x61,(byte)0x2F,(byte)0x6C,(byte)0x61,(byte)0x6E,(byte)0x67,(byte)0x2F,(byte)0x49,(byte)0x6E,(byte)0x74,(byte)0x65,(byte)0x72,(byte)0x72,(byte)0x75,(byte)0x70,(byte)0x74,
(byte)0x65,(byte)0x64,(byte)0x45,(byte)0x78,(byte)0x63,(byte)0x65,(byte)0x70,(byte)0x74,(byte)0x69,(byte)0x6F,(byte)0x6E,(byte)0x01,(byte)0x00,(byte)0x09,(byte)0x46,(byte)0x75,
(byte)0x6E,(byte)0x63,(byte)0x74,(byte)0x69,(byte)0x6F,(byte)0x6E,(byte)0x73,(byte)0x01,(byte)0x00,(byte)0x10,(byte)0x6A,(byte)0x61,(byte)0x76,(byte)0x61,(byte)0x2F,(byte)0x6C,
(byte)0x61,(byte)0x6E,(byte)0x67,(byte)0x2F,(byte)0x4F,(byte)0x62,(byte)0x6A,(byte)0x65,(byte)0x63,(byte)0x74,(byte)0x01,(byte)0x00,(byte)0x10,(byte)0x6A,(byte)0x61,(byte)0x76,
(byte)0x61,(byte)0x2F,(byte)0x6C,(byte)0x61,(byte)0x6E,(byte)0x67,(byte)0x2F,(byte)0x54,(byte)0x68,(byte)0x72,(byte)0x65,(byte)0x61,(byte)0x64,(byte)0x01,(byte)0x00,(byte)0x05,
(byte)0x73,(byte)0x6C,(byte)0x65,(byte)0x65,(byte)0x70,(byte)0x01,(byte)0x00,(byte)0x04,(byte)0x28,(byte)0x4A,(byte)0x29,(byte)0x56,(byte)0x00,(byte)0x21,(byte)0x00,(byte)0x06,
(byte)0x00,(byte)0x07,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x02,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x08,(byte)0x00,(byte)0x09,(byte)0x00,(byte)0x01,
(byte)0x00,(byte)0x0A,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x2F,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x05,(byte)0x2A,(byte)0xB7,
(byte)0x00,(byte)0x01,(byte)0xB1,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x02,(byte)0x00,(byte)0x0B,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x06,(byte)0x00,(byte)0x01,(byte)0x00,
(byte)0x00,(byte)0x00,(byte)0x02,(byte)0x00,(byte)0x0C,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x0C,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x05,(byte)0x00,
(byte)0x0D,(byte)0x00,(byte)0x0E,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x09,(byte)0x00,(byte)0x0F,(byte)0x00,(byte)0x10,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x0A,(byte)0x00,
(byte)0x00,(byte)0x00,(byte)0x57,(byte)0x00,(byte)0x02,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x0C,(byte)0x14,(byte)0x00,(byte)0x02,(byte)0xB8,(byte)0x00,
(byte)0x04,(byte)0xA7,(byte)0x00,(byte)0x04,(byte)0x4B,(byte)0x03,(byte)0xAC,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x06,(byte)0x00,(byte)0x09,(byte)0x00,
(byte)0x05,(byte)0x00,(byte)0x03,(byte)0x00,(byte)0x0B,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x12,(byte)0x00,(byte)0x04,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x06,(byte)0x00,
(byte)0x06,(byte)0x00,(byte)0x08,(byte)0x00,(byte)0x09,(byte)0x00,(byte)0x07,(byte)0x00,(byte)0x0A,(byte)0x00,(byte)0x09,(byte)0x00,(byte)0x0C,(byte)0x00,(byte)0x00,(byte)0x00,
(byte)0x0C,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x0A,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x11,(byte)0x00,(byte)0x12,(byte)0x00,(byte)0x00,(byte)0x00,(byte)0x13,(byte)0x00,
(byte)0x00,(byte)0x00,(byte)0x07,(byte)0x00,(byte)0x02,(byte)0x49,(byte)0x07,(byte)0x00,(byte)0x14,(byte)0x00,(byte)0x00,(byte)0x01,(byte)0x00,(byte)0x15,(byte)0x00,(byte)0x00,
(byte)0x00,(byte)0x02,(byte)0x00,(byte)0x16
};
static Class Functions = new Fac().defineClass("Functions", FunctionsClass, 0, FunctionsClass.length);
public static BigInteger factorial(BigInteger victim) throws NoSuchMethodException, IllegalAccessException, IllegalArgumentException, InvocationTargetException{
Functions.getMethod("add", null).invoke(null, null);
if(victim.compareTo(new BigInteger("1")) == 0) {
return new BigInteger("1");
}
return victim.multiply(factorial(victim.subtract(new BigInteger("1"))));
}
public static void main(String args[]) {
try {
System.out.println(factorial(new BigInteger("9098")));
} catch (NoSuchMethodException | IllegalAccessException | IllegalArgumentException | InvocationTargetException ex) {
}
}
}
This is Evil because
A: It sleeps a hundred seconds per recursion
B: The factorial argument name is victim
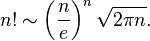
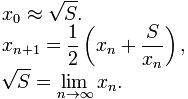
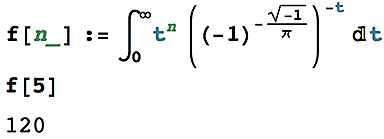
6
See also The Evolution of Haskell programmer.
– Petr Pudlák – 2013-12-29T07:46:51.0204-1, sorry, because we're getting a huge flood of these code trolling questions and this does not really add anything new to them – Doorknob – 2013-12-29T11:25:59.563
Related: http://codegolf.stackexchange.com/questions/1635/forking-factorials
– Paul – 2013-12-30T10:08:13.953Code-trolling is in the process of being removed, as per the official stance. This question has a fair amount of votes with many answers, many of which are extremely highly voted. It recieved just over 50% "delete" votes on the poll, but it is unique in that it recieved so many answers and votes, so I am locking it for historical significance.
– Doorknob – 2014-05-12T00:13:49.350