Professor at MIT can read minds!

Question

The task is taken from an MIT lecture by Prof. Devadas called You can read minds. A detailed explanation of the trick can be found in the linked video, or in this document. I'll try to explain it in simpler terms.

It turns out this was invented in the 1930's, and is known as the "Five-Card Trick of Fitch Cheney".

---

The trick goes like this:

• Five random cards are chosen from a deck of cards. The audience and your assistant get to see them, but you don't.
• Your assistant (with whom you have practiced) will select four of those cards and show them to you in a specific order. Note that the hidden card is not randomly picked from the 5 cards. The assistant picks a/the card that will make the trick work.
• You will deduce, based on the information you can gather from the four cards what the fifth card is.

---

How?

Keep the following two points in mind:

1. When choosing 5 random cards, you are guaranteed that at least two cards have the same suit¹.

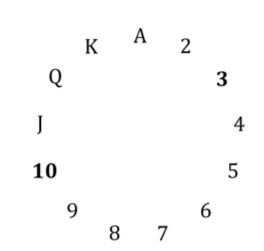
2. The image below shows a circle with all the ranks². Since it's a circle, it's possible to count: J, Q, K, A, 2, 3 (i.e. modular counting). You are guaranteed that the hidden card does not have the same rank as the first, since they will be of the same suit (explained below). It's always possible to choose the first card and the hidden cards such that the hidden card is between 1 and 6 ranks higher than the first (when counting in circles). If the first card is 1, then the hidden card will be 2,3,4,5,6 or 7. If the first card is J, then the hidden card will be Q,K,A,2,3 or 4 and so on.

---

The algorithm:

The first card: This card will have the same suit as the hidden card. The card will also be the reference point you'll use when figuring out the rank of the hidden card.

The 2nd, 3rd and 4th cards decodes a value in the inclusive range 1 ... 6. We'll call the three cards S, M, L (smallest card, middle card, largest card). The values will be encoded like this (lexicographic order):

S M L   -> 1
S L M   -> 2
M S L   -> 3   
M L S   -> 4
L S M   -> 5
L M S   -> 6 

So, if the rank of the first card is 5, and the remaining three cards have ranks 4 Q 7 (they are ordered S L M), then the last card has rank 5+2=7. You may choose if the ace should be the highest or lowest card, as long as it's consistent.

If several cards share rank, then the suit will determine the order, where C < D < H < S.

---

Input format:

The four cards will be given as H3 (three of hearts), DK (King of diamonds) and so on. You may choose to take the input the other way around as 3H and KD instead.

The input can be on any convenient format, but you can't combine the list of suits in one variable and the list of ranks in another. 'D5', 'H3' .. and [['D',5],['H',3] ... are both OK, but 'DHCH',[5,3,1,5] is not. You can't use numbers instead of letters, except for T.

Output

The hidden card, in the same format as the input.

---

Example

Let's do a walkthrough:

Input:
D3 S6 H3 H9

We know the hidden card is a diamond, since the first card is a diamond. We also know that the rank is 4,5,6,7,8 or 9 since the rank of the first card is 3.

The remaining cards are ordered 6,3,9 ==> M,S,L, which encodes the value 3. The hidden card is therefore 3+3=6 of diamonds, thus the output should be D6.

Test cases:

C3 H6 C6 S2
C9            # The order is LMS (H6 > C6, and 2 < 6). 3+6=9     

SQ S4 S3 ST   # (ST = S10. Format is optional)
S2            # The order is MSL. 12+3=2

HA CA DA SA
H2            # The order is SML. 14+1=2

---

This is code-golf, so the shortest solution in each language wins. Explanations are encouraged!

---

¹There are four suits (Clubs, Diamonds, Hearts and Spades).

²There are 13 ranks, 2,3,4,5,6,7,8,9,10,J,Q,K,A. You may choose to use T instead of 10.

Answer 1

JavaScript (ES6), 130 102 bytes

Takes input as an array of strings in "Rs" format, where R is the rank and s is the suit. Expects "T" for 10's. Aces are low.

a=>(s='A23456789TJQK')[([[R,[,S]],B,C,D]=a.map(c=>[s.search(c[0])+14,c]),R+=D<C|2*((D<B)+(C<B)))%13]+S

Try it online!

How?

We first convert each card into an array [rank, card] where rank is a numeric value in [14...26] and card is the original string.

[[R, [, S]], B, C, D] = a.map(c => ['A23456789TJQK'.search(c[0]) + 14, c])

The rank and suit of the first card are stored in R and S respectively. The three other cards are stored in B, C and D.

For instance, ['3c','6h','6c','2s'] becomes:

[ [ 16, '3c' ], [ 19, '6h' ], [ 19, '6c' ], [ 15, '2s' ] ]
    ^^    ^     <---------->  <---------->  <---------->
    R     S          B             C             D

We then compare each pair in [ B, C, D ]. These elements are implicitly coerced to strings when they are compared with each other:

[ 19, '6h' ] --> '19,6h'

Because both rank and card are guaranteed to consist of exactly two characters, it is safe to compare in lexicographical order.

We compute:

(D < C) | 2 * ((D < B) + (C < B))

Below are all the possible combinations:

 B, C, D | v0 = D < B  | v1 = C < B  | v2 = D < C  | v2|2*(v0+v1)
---------+-------------+-------------+-------------+--------------
 S, M, L |    false    |    false    |    false    |      0
 S, L, M |    false    |    false    |    true     |      1
 M, S, L |    false    |    true     |    false    |      2
 M, L, S |    true     |    false    |    true     |      3
 L, S, M |    true     |    true     |    false    |      4
 L, M, S |    true     |    true     |    true     |      5

Finally, we build the output card using R, S and the above result:

'A23456789TJQK'[(R += D < C | 2 * ((D < B) + (C < B))) % 13] + S

Answer 2

Python 2, 143 140 138 136 127 125 124 123 121 bytes

lambda(S,V),*l:S+N[F(V)+int(`map(sorted(l,key=lambda(s,v):(F(v),s)).index,l)`[1::3],3)*3/10]
N='23456789TJQKA'*2;F=N.find

Try it online!

Aces are high

---

Encodes the three cards by finding their position in a sorted list of the cards (0=smallest, 1=middle, 2=largest):

cards:   [SK, C4, H4]
sorted:  [C4, H4, SK]

ranks:   [ 2            index of SK in sorted
ranks:   [ 2,  0        index of C4 in sorted
ranks:   [ 2,  0,  1    index of H4 in sorted
ranks:   [ 2,  0,  1] = L,S,M

This is converted to an integer in base 3 and multiplied by 3, and divided by 10:

int('201',3) = 19 -> 19*3//10 = 5

The different encodings are:

cards            base3    *3   /10
[0, 1, 2]  012     5      15     1
[0, 2, 1]  021     7      21     2
[1, 0, 2]  102     11     33     3
[1, 2, 0]  120     15     45     4
[2, 0, 1]  201     19     57     5
[2, 1, 0]  210     21     63     6

---

Saved:

• -2 bytes, thanks to ovs

Answer 3

Jelly, 33 bytes

ØDḊḊ;“TJQKA”p“CDHS”
¢iⱮµḊŒ¿×4+Ḣị¢

Try it online!

Explanation

The first line is niladic. It yields a list of the 52 cards

ØDḊḊ;“TJQKA”p“CDHS”
ØD                   Digits: '0123456789'
  ḊḊ                 Dequeue twice: '23456789'
    ;                Append with...
     “TJQKA”         ...the string 'TJQKA': '23456789TJQKA'. These are the ranks
            p        Cartesian product with...
             “CDHS”  ...the suits.
                     This yields the list of all cards in lexicographic order:
                                 ['2C', '2D', '2H', '2S',
                                  '3C', ...         'AS']

In the main link, ¢ calls the result of the first link which is the list of cards.

¢iⱮµḊŒ¿×4+Ḣị¢
¢              List of cards
 iⱮ            Index of each (Ɱ) of the inputs in the list.
   µ           New monadic link. The list of indices become this links argument.
    Ḋ          Remove the first one.
     Œ¿        Index of the permutation of the last three items. Gives a number 1-6
               as described in the problem statement.
       ×4      Multiply this by 4 so that when we add to the index of the first
               card we end up in the same suit.
         +Ḣ    Add the first index.
           ị   Use this number to index into...
            ¢  ...the list of cards.

Answer 4

APL (Dyalog Unicode), 49 bytes^SBCS

⊃x⌽⍨⊃i-4×2-⌊1.8⊥⍋1↓i←⎕⍳⍨x←,⍉'CDHS'∘.,2↓⎕D,'TJQKA'

Try it online!

Overview: 'CDHS'∘.,2↓⎕D,'TJQKA' generates the outer product, so a 2d matrix with (C2 C3 C4 ...), (D2 D3 D4 ...), .... We then transpose this matrix to get (C2 D2 H2 ...), ... and then flatten that.

Thanks to @ngn for the 2-⌊1.8⊥, which takes the order of cards (SML=1 2 3) and grades them (like the 1 to 6 in the OP).

Code explanation:

⊃x⌽⍨⊃i-4×2-⌊1.8⊥⍋1↓i←⎕⍳⍨x←,⍉'CDHS'∘.,2↓⎕D,'TJQKA'
                                       ⎕D,'TJQKA' ⍝ Concatenate a list of numbers with TJQKA
                                     2↓           ⍝ Drop 2 (removes "01")
                                  ∘.,             ⍝ Generate the outer product of this prefixed with
                            'CDHS'                ⍝ The suits
                           ⍉                      ⍝ Invert rows/columns
                          ,                       ⍝ Flatten (matrix -> array)
                        x←                        ⍝ Store in x
                      ⍳⍨                          ⍝ Inverted ⍳⍨: find the indices, in our cards,
                     ⎕                            ⍝ of the argument cards
                   i←                             ⍝ Store these indices in i
                 1↓                               ⍝ Remove the first index
                ⍋                                 ⍝ Grade: get ordered indices
         2-⌊1.8⊥                                  ⍝ The magic happens here: get the number from 1 to 6
       4×                                         ⍝ Multiply by 4 to get the same "back" on the card
    ⊃i-                                           ⍝ Substract the result from our first index (which we had discarded)
⊃x⌽⍨                                              ⍝ (Modulated) Index into x (our cards) with this value

Answer 5

Retina, 218 208 bytes

[JQK]
1$&
T`AJQK`1123
*' G0`
\d+
5**
' G, 1,`
T`CD\HS`d
\d
*
/^(_+)¶\1/(/¶(_+)¶\1/(K`1
/^(_+)¶_+¶\1/(K`2
))K`4
/^(_+)¶_+¶\1/(K`3
/¶(_+)¶\1/(K`5
)))K`6
\d
$+3-$&
(\d+)-(\d+)
$1*_$2*
_{13}(_+)|(_{1,13})
$.($1$2

Try it online!

Explanation:

[JQK]
1$&
T`AJQK`1123

Replaces Aces, Jacks, Queens and Kings with 1, 11, 12 and 13. The first two lines prepend a 1 before the letter, and the last transliterates the second digit.

*' G0`

The * indicates that this stage should not modify the working string. This may make the stage seem pointless, but it will be useful later. The ' splits the working string at every space, and G0 takes the first one (so it finds the first card).

\d+
5**
' G, 1,`'

The first two lines multiply the numbers on the cards by 5, then turn them into unary (for example, 5 is represented as _____), so that we can add smaller amounts for suits later. The final line splits on spaces and keeps the last three cards.

T`CD\HS`d
\d
*

This converts Clubs, Diamonds, Hearts and Spades to 0, 1, 2 and 3 respectively, and turns the number into unary. Since it is now on the attached of the number part of the card, it will give a unique value for the card, determining how high it is.

/^(_+)¶\1/(/¶(_+)¶\1/(K`1
/^(_+)¶_+¶\1/(K`2
))K`4
/^(_+)¶_+¶\1/(K`3
/¶(_+)¶\1/(K`5
)))K`6

This finds the ordering of the cards, and the value to add to the first card. For example, on the first line /^(_+)¶\1_+/( matches orders that have the middle value larger than the first value. It creates an if-else loop for what to do (as this order matches permutations 1, 2 and 4). K marks a constant.

\d
$+3-$&

Remember earlier when we used * to indicate that a stage wouldn't affect the working string? This is where we use it. This stage is a replace stage; it replaces the number to add by $+3-$&. $+3 accesses the * stage, and gets the suit and number of the first card, - acts as a seperator, and $& is the match. So the working string is now {suit}{original number}-{number to add}

(\d+)-(\d+)
$1*_$2*

This turns the two numbers into unary and adds them together.

_{13}(_+)|(_{1,13})
$.($1$2

The top line captures either the number or the number - 13 (so that we don't get outputs of e.g S16). The bottom line turns the captured number back into base 10, and the result is printed implicitly.

Answer 6

Charcoal, 64 62 bytes

≔⪪⭆⁺⭆⁸⁺²ιTJQKA⭆CDHS⁺λι²δ≔Ｅ⟦ηζε⟧⌕διυ§δ⁺⌕δθ×⁴⊕⁺∧⌕υ⌊υ⊗⊕¬⌕υ⌈υ‹⊟υ⊟υ

Try it online! Link is to verbose version of code. Uses T for 10 and sorts A high. The permutation index was not very easily decoded; a different permutation order would have saved me at least three bytes. Explanation:

⁺⭆⁸⁺²ιTJQKA

Add 2 to all the integers 0 to 7, then concatente them and suffix TJQKA for the picture cards and ace. This saves 2 bytes over a string literal, although it turns out that having A high would have saved a byte through string compression anyway.

≔⪪⭆...⭆CDHS⁺λι²δ

Map over the cards and the suits, concatenting the two together. Since this would normally produce a nested array, the results are instead concatenated into a single string which is then split up into pairs of characters again.

≔Ｅ⟦ηζε⟧⌕διυ

Find the positions of the second, third and fourth cards.

⊕⁺∧⌕υ⌊υ⊗⊕¬⌕υ⌈υ‹⊟υ⊟υ

Compute the 1-indexed permutation index. The first two permutations have the smallest card first; this is tested via ⌕υ⌊υ. The other two pairs of permutations are differentiated as to whether the largest card is first; this is tested via ⌕υ⌈υ. Logical and arithmetic operations then map these tests to the values 0, 2 and 4; this is then increased by 1 depending on the comparison between the third and fourth cards, tested via ‹⊟υ⊟υ. Finally the index is incremented to give the desired encoding.

§δ⁺⌕δθ×⁴...

Multiply that by 4 repesenting the distance between cards of the same suit, add on the position of the first card, and cyclically index and print the result.

Answer 7

Python 2, 147 bytes

lambda a:a[0][0]+R[h(map(a[1:].index,sorted(a[1:],key=lambda c:(I(c[1]),c))))+I(a[0][1])]
R='A23456789TJQK'*2;I=R.index
h=lambda(x,y,z):x*2+(y>z)+1

Try it online!

Answer 8

Pyth, 42 bytes

+hhQ@J+`M}2Tmk"JQKA"+hhKm,xJtdhdQhx.pStKtK

Really ugly...

Try it online: Demontration or Test Suite

Answer 9

J, 68 bytes

r=.'23456789TJQKA'
{:@{.,~0{r|.~1+(r i.0{{.)+(>,{r;'CDHS')A.@/:@i.}.

Try it online!

Note: -3 off TIO bytes because the f=. doesn't count. Will attempt to golf further and add explanation tomorrow.

Answer 10

JavaScript (Node.js), 124 bytes

s=>(k='23456789TJQKA')[p=t=>k.search(s[t][0])+32+s[t][1],u=p(0),(u[0]+u[1]-2*(p(1)<p(2))-2*(p(1)<p(3))-(p(2)<p(3)))%13]+u[2]

Try it online!

JavaScript (Node.js), 125 bytes

s=>(k='23456789TJQKA')[p=s.map(t=>k.search(t[0])+32+t[1]),u=p[0],(u[0]+u[1]-2*(p[1]<p[2])-2*(p[1]<p[3])-(p[2]<p[3]))%13]+u[2]

Try it online!

Answer 11

T-SQL, 198 bytes

Input is a table variable. Using T for 10, aces are low

Format for cards rank/suit KH,6D,TS

DECLARE @ TABLE(c char(2),i int identity(4,-1))
INSERT @
VALUES('2C'),('5H'),('4S'),('3C')

SELECT 
substring(max(h+h),max(charindex(q,h)*w)+sum(power(3,i)*r)/10-4,1)+max(right(c,w))FROM(SELECT
rank()over(order by
w,charindex(q,h))%4r,*FROM(SELECT'A23456789TJQK'h,i/4w,left(c,1)q,*FROM @)d)y

Try it online ungolfed

Notice how the SML(1-6) value is calculated:

Logically S,M,L(1,2,3) is converted to a numeric value

first card is valued 27*sequence value

second card is valued 9*sequence value

third card is valued 3*sequence value

Answer 12

05AB1E, 37 bytes

2TŸ.•3u§•S«.•ôì•âíJuDIkćsD{œJsJk>4*+è

Port of @dylnan's Jelly answer, but unfortunately 05AB1E doesn't have the permutation index builtin..

Try it online or verify all test cases.

Explanation:

2TŸ                # Push the list [2,3,4,5,6,7,8,9,10]
   .•3u§•S         # Push compressed string "jqka", converted to a list of characters
          «        # Merge the lists together
.•ôì•              # Push compressed string "cdhs"
     â             # Create each possible pair
      í            # Reverse each pair
       Ju          # Join each pair together, and convert to uppercase
D                  # Duplicate the deck
 Ik                # Get the index of the cards of the input-list in the deck
   ć               # Extract head; pop and push remainder and head
    s              # Swap to get the remainder
     D{            # Create a sorted copy
       œ           # Get the permutations of that
        JsJk       # Get the index of the unsorted permutation in this permutations list
            >      # Increase it by 1 (since 05AB1E has 0-based indexing)
             4*    # Multiply it by 4
               +   # Add it to the extracted head
                è  # And index it into the duplicated deck
                   # (after which the result is output implicitly)

See this 05AB1E tip of mine (section How to compress strings not part of the dictionary?) to understand why .•3u§• is "jqka" and .•ôì• is "cdhs".