Find the longest uninterrupted arc in N dimensions

Question

See similar question for 2D case: Find the longest uninterrupted arc

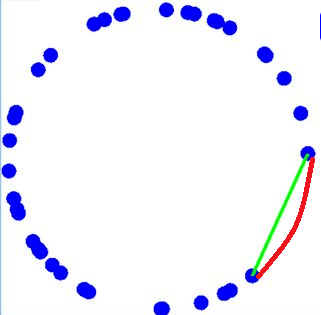
The challenge here is to find the longest uninterruped great circle arc around a unit hypersphere in N dimensions, with a random amount of hyperspheres distributed in random positions around it. Here is a diagram in two dimensions to assist my explanation:

All hyperspheres around the edge have a radius of 0.5, although in this diagram, for illustration purposes only, they are smaller.

The distance of every hypersphere from the origin at the centre is 1.

The red line indicates the largest arc between any two hyperspheres that is not interrupted by any other hypersphere. The challenge is to find the two points on either end of the red line. The green line is simply the straight line distance.

A clarification about what interrupted means: When drawing an arc around the edge of the unit hypersphere of radius 1 (the red line), this arc should not be intersected by any other hypersphere.

Your function should take an array of double[][] and return the indices of the two hyperspheres with the largest uninterrupted arc.

int[] FindPair(double[][] points)
{
   return new[]{ 0, 1}; //Find the indices of the two points
}

The points array contains all of the positions of the hyperspheres in N dimensions, for example:

points[i] = {x, y} //2D
points[i] = {x, y, z} //3D
points[i] = {x, y, z, a} //4D
...

Extra clarification:

• All points in the input define a circle, sphere or hypersphere with a diameter of 1 (radius 0.5)
• The two points outputted define the start and end of an arc drawn around the edge of a hypersphere with origin 0,0 and radius 1. (Great circle arc).
• If any other hypersphere than the two outputted hyperspheres intersects the arc then the solution is invalid.
• You can assume that the distance from the origin of all given hyperspheres is 1.
• If there is no valid solution (all arcs are intersected by other hyperspheres) then the function should output an empty array
• Arcs between two points which are perfectly antipodal should be disregarded, since there exist infintely many great circle arcs between antipodal points
• Do not worry about cases in less than two dimensions
• For purposes of numerical error, you can assume that epsilon is 1e-16. This means that you can assume that the result is not changed if the input is changed not more than 1e-16.

The answer with the smallest Big O algorithm complexity wins. In case of a tie, shorter code wins.

Test case 1 (2D):

Points: {
  { -0.71997 , -0.69400 },
  { 0.88564 , 0.46437 },
  { 0.78145 , -0.62397 },
  { 0.98409 , -0.17765 },
  { 0.88220 , 0.47087 },
  { 0.69938 , 0.71475 },
  { -0.89036 , -0.45526 },
  { -0.70588 , -0.70833 },
  { 0.70507 , 0.70914 },
  { -0.34971 , 0.93686 }
}

There is only one valid arc here which is:
{2, 3}

Test case 2 (2D):

Points: {
  { -0.71038 , 0.70382 },
  { 0.04882 , 0.99881 },
  { -0.53250 , -0.84643 },
  { -0.86814 , -0.49632 },
  { 0.97588 , -0.21829 },
  { 0.73581 , -0.67719 },
  { 0.88413 , -0.46724 },
  { -0.28739 , -0.95781 },
  { -0.68325 , 0.73019 },
  { 0.91879 , 0.39475 },
  { 0.65335 , 0.75706 },
  { -0.21009 , -0.97768 },
  { -0.94542 , -0.32585 },
  { 0.83207 , -0.55467 },
  { 0.99482 , 0.10170 },
  { 0.86228 , 0.50643 },
  { 0.98017 , 0.19817 },
  { 0.67520 , 0.73763 },
  { -0.03982 , -0.99921 },
  { -0.57624 , -0.81728 }
}

Again only one valid arc which is:
{0, 8}

Test case 3:(3D)

Points = {
    { 0.01973 , -0.99317 , -0.11502 },
    { -0.71738 , -0.67848 , 0.15822 },
    { 0.84743 , -0.50733 , -0.15646 },
    { 0.87628 , 0.25076 , 0.41140 },
    { -0.48299 , 0.50965 , -0.71202 },
    { 0.69096 , 0.57799 , -0.43417 },
    { 0.51743 , 0.67876 , 0.52110 },
    { 0.78261 , -0.45122 , -0.42886 },
    { 0.40781 , -0.46859 , -0.78366 },
    { 0.65068 , -0.64966 , 0.39314 },
    { -0.09253 , 0.95421 , 0.28447 },
    { -0.01408 , 0.38357 , 0.92340 },
    { 0.57281 , 0.65041 , -0.49885 },
    { 0.19617 , -0.24506 , -0.94945 },
    { -0.51822 , 0.34419 , 0.78293 },
    { 0.46704 , -0.14902 , 0.87159 },
    { -0.71731 , 0.68775 , 0.11162 },
    { -0.37867 , -0.17063 , 0.90967 },
    { -0.75267 , 0.03982 , 0.65719 },
    { -0.56779 , 0.34520 , -0.74730 }
}

There are 19 valid arcs here, the largest of which is:
Answer: {1, 9}

Test case 4: (4D)

Points = {
    { -0.29024 , 0.35498 , -0.79921 , -0.79921 },
    { -0.62641 , 0.38217 , -0.54689 , -0.54689 },
    { -0.15500 , 0.97029 , -0.14852 , -0.14852 },
    { 0.39689 , 0.40861 , -0.68332 , -0.68332 },
    { 0.71300 , -0.29992 , -0.60949 , -0.60949 },
    { 0.49510 , 0.64115 , 0.30312 , 0.30312 },
    { -0.01944 , -0.94146 , 0.07992 , 0.07992 },
    { 0.50442 , -0.42007 , -0.44106 , -0.44106 },
    { 0.12829 , 0.34220 , -0.62093 , -0.62093 },
    { -0.60989 , -0.52113 , -0.58193 , -0.58193 },
    { 0.21290 , 0.50385 , 0.66164 , 0.66164 },
    { -0.63566 , 0.04453 , 0.18066 , 0.18066 },
    { -0.02630 , 0.86023 , 0.50700 , 0.50700 },
    { 0.90530 , 0.08179 , -0.41634 , -0.41634 },
    { 0.49062 , -0.51654 , 0.43727 , 0.43727 },
    { -0.56405 , 0.57448 , -0.32617 , -0.32617 },
    { 0.14677 , -0.14756 , 0.77293 , 0.77293 },
    { -0.16328 , -0.37123 , 0.49193 , 0.49193 },
    { -0.46471 , 0.07951 , 0.43186 , 0.43186 },
    { -0.54567 , 0.43537 , -0.49301 , -0.49301 }
}
There are 16 valid arcs here, the largest of which is:
Answer: {9, 17}

Answer 1

The best solution I have found so far. Involves sampling points. Any suggestions for improvement would be appreciated. It is also the algorithm I have used to generate the test cases, so if it is incorrect, the test cases may be incorrect.

C#, O(N^3), lots of bytes

    private const double Epsilon = 1e-16;

    public static int[] Find(double[][] points)
    {
        var p1 = 0;
        var p2 = 0;
        var maxDist = 0d;
        //Compare each sphere with each other sphere
        for (var i = 0; i < points.Length - 1; i++)
        {
            for (var j = i + 1; j < points.Length; j++)
            {
                var d = FindMaxDist(points, i, j, 100);
                if (d > maxDist)
                {
                    p1 = i;
                    p2 = j;
                    maxDist = d;
                }
            }
        }

        if (maxDist > 0)
        {
            return new[] { p1, p2 };
        }
        return new int[] { };
    }

    private static double FindMaxDist(double[][] points, int p1, int p2, int sampleCount)
    {

        var originalDist = Dist(points[p1], points[p2]);

        //Disregard antipodal points
        if (originalDist > 2-Epsilon)
            return 0;

        var dimensions = points[0].Length;
        var vector = new double[dimensions];

        //Find the straight line vector between the two points
        for (var j = 0; j < dimensions; j++)
            vector[j] = (points[p1][j] - points[p2][j]);

        //Generate samples along the arc
        var pointSamples = new double[sampleCount][];
        for (var i = 0; i < sampleCount; i++)
        {
            pointSamples[i] = new double[dimensions];
            //Clone the vector before resizing to avoid numerical error due to multiple resizes
            var newV = ClonePoint(vector);
            //How far are we along the line between the two points depending on the current sample number?
            var newLength = (1 / ((double)sampleCount + 1)) * (i+1) * originalDist;
            ResizeVector(newV, newLength);

            //Set the position of the sample
            for (var j = 0; j < dimensions; j++)
                pointSamples[i][j] = points[p1][j] - newV[j];

            //The sample will lie on a straight line between the two points, not an arc
            //Scale it so that it lies a distance of 1 from the origin, in order to be on the arc
            ResizeVector(pointSamples[i]);
        }

        //Now simply check the samples for intersections
        for (var i = 0; i < sampleCount; i++)
        {
            for (var j = 0; j < points.Length; j++)
            {
                if (j == p1 || j == p2)
                    continue;

                var d = Dist(points[j], pointSamples[i]);
                if (d < 0.5)
                    return 0;
            }
        }
        return originalDist;
    }

    //The distance between two points
    public static double Dist(double[] d1, double[] d2)
    {
        double dist = 0;
        for (var i = 0; i < d1.Length; i++)
        {
            var diff = d1[i] - d2[i];
            dist += diff * diff;
        }
        return Math.Sqrt(dist);
    }

    public static double[] ClonePoint(double[] point)
    {
        var p = new double[point.Length];
        Array.Copy(point, p, point.Length);
        return p;
    }


    public static void ResizeVector(double[] pos, double targetLength = 1)
    {
        var currentLength = VectorLength(pos);
        var scale = targetLength / currentLength;
        for (var i = 0; i < pos.Length; i++)
            pos[i] *= scale;
    }

    public static double VectorLength(double[] vector)
    {
        double length = 0;
        for (var i = 0; i < vector.Length; i++)
            length += vector[i] * vector[i];
        return Math.Sqrt(length);
    }