Triangular Lattice Points close to the Origin

Question

Background

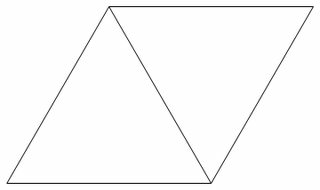
A triangular grid is a grid formed by tiling the plane regularly with equilateral triangles of side length 1. The picture below is an example of a triangular grid.

A triangular lattice point is a vertex of a triangle forming the triangular grid.

The origin is a fixed point on the plane, which is one of the triangular lattice points.

Challenge

Given a non-negative integer n, find the number of triangular lattice points whose Euclidean distance from the origin is less than or equal to n.

Example

The following figure is an example for n = 7 (showing only 60-degree area for convenience, with point A being the origin):

Test Cases

Input | Output
---------------
    0 |       1
    1 |       7
    2 |      19
    3 |      37
    4 |      61
    5 |      91
    6 |     127
    7 |     187
    8 |     241
    9 |     301
   10 |     367
   11 |     439
   12 |     517
   13 |     613
   14 |     721
   15 |     823
   16 |     931
   17 |    1045
   18 |    1165
   19 |    1303
   20 |    1459
   40 |    5815
   60 |   13057
   80 |   23233
  100 |   36295
  200 |  145051
  500 |  906901
 1000 | 3627559

Hint: This sequence is not OEIS A003215.

Rules

Standard rules for code-golf apply. The shortest submission wins.

Please include how you solved the challenge in your submission.

Answer 1

Python 2, 43 bytes

f=lambda n,a=1:n*n<a/3or n*n/a*6-f(n,a+a%3)

Try it online!

This is black magic.

Offering 250 rep for a written-up proof. See Lynn's answer for a proof and explanation.

Answer 2

Haskell, 48 bytes

f n=1+6*sum[(mod(i+1)3-1)*div(n^2)i|i<-[1..n^2]]

Try it online!

Uses xnor's "black magic" formula:

$$f(n)=1+6\sum_{a=0}^\infty \left\lfloor \frac{n^2}{3a+1}\right\rfloor - \left\lfloor \frac{n^2}{3a+2}\right\rfloor$$

A proof of its correctness, and an explanation of how xnor managed to express it in 43 bytes of Python, can be found here.

Long story short: we count Eisenstein integers of norm \$1 \le N \le n^2\$, by factoring \$N = (x+y\omega)(x+y\omega^*)\$ into Eisenstein primes and counting how many solutions for \$(x,y)\$ come out of the factorization. We recognize the number of solutions as being equal to

$$6 \times ((\text{# of divisors of }N \equiv 1\space(\text{mod }3)) - (\text{# of divisors of }N \equiv 2\space(\text{mod }3)))$$

and apply a clever trick to make that really easy to compute for all integers between \$1\$ and \$n^2\$ at once. This yields the formula above. Finally, we apply some Python golf magic to end up with the really tiny solution xnor found.

Answer 3

Wolfram Language (Mathematica), 53 51 50 bytes

^{-1 byte thanks to @miles}

Sum[Boole[x(x+y)+y^2<=#^2],{x,-2#,2#},{y,-2#,2#}]&

Try it online!

How?

Instead of thinking in this:

Think of it like this:

So we apply the tranformation matrix [[sqrt(3)/2, 0], [1/2, 1]] to transform the second figure to the first one.

Then, we must find the circle in the triangular grid in terms of Cartesian coordinates.

(sqrt(3)/2 x)^2 + (1/2 x + y)^2 = x^2 + x y + y^2

So we find lattice points x, y such that x^2 + x y + y^2 <= r^2

For example, with r = 3:

Answer 4

Wolfram Language (Mathematica), 48 bytes

Based on OEIS A004016.

1+6Sum[DivisorSum[i,#~JacobiSymbol~3&],{i,#^2}]&

Try it online!

Answer 5

CJam (24 bytes)

{_*_,f{)_)3%(@@/*}1b6*)}

This is an anonymous block (function) which takes one argument on the stack and leaves the result on the stack. Online test suite. Note that the two largest cases are too slow.

Explanation

alephalpha noted in a comment on the question that

It is the sum of the first n^2+1 terms of OEIS A004016

and xnor's answer implements this sum (although I'm not sure whether their unposted proof uses it explicitly) as $$f(n) = 1 + 6 \sum_{a=0}^\infty \left\lfloor\frac{n^2}{3a+1}\right\rfloor - \left\lfloor\frac{n^2}{3a+2}\right\rfloor$$

My proof of correctness of that formula is based on some information gleaned from alephalpha's OEIS link:

G.f.: 1 + 6*Sum_{n>=1} x^(3*n-2)/(1-x^(3*n-2)) - x^(3*n-1)/(1-x^(3*n-1)). - Paul D. Hanna, Jul 03 2011

for which the relevant reference is the paper by Hirschhorn. An elementary proof is possible using nothing more than a basic understanding of complex numbers (cube roots of unity, magnitude), the concept of generating functions, the derivative of \$x^a\$, and the chain rule of differentiation. In summary, we first prove from first principles the Jacobi triple-product identity $$\prod_{k=0}^\infty (1-q^{k+1})(1 + xq^{k+1})(1 + x^{-1}q^k) = \sum_{k\in \mathbb{Z}} q^{k(k+1)/2}x^k$$ That then bootstraps a proof that $$\sum_{m,n \in \mathbb{Z}} \omega^{m-n} q^{m^2+mn+n^2} = \prod_{k=1}^\infty \frac{(1-q^k)^3}{1-q^{3k}}$$ where \$\omega\$ is a primitive cube root of unity. The final big step is to use this to show that $$\sum_{m,n \in \mathbb{Z}} q^{m^2+mn+n^2} = 1 + 6 \sum_{k \ge 0} \left(\frac{q^{3k+1}}{1-q^{3k+1}} - \frac{q^{3k+2}}{1-q^{3k+2}} \right)$$

Code dissection

{          e# Define a block. Stack: ... r
  _*       e#   Square it
  _,f{     e#   Map with parameter: invokes block for (r^2, 0), (r^2, 1), ... (r^2, r^2-1)
    )      e#     Increment second parameter. Stack: ... r^2 x with 1 <= x <= r^2
    _)3%(  e#     Duplicate x and map to whichever of 0, 1, -1 is equal to it (mod 3)
    @@/*   e#     Evaluate (r^2 / x) * (x mod 3)
  }
  1b6*     e#   Sum and multiply by 6
  )        e#   Increment to count the point at the origin
}

Answer 6

J, 27 bytes

[:+/@,*:>:(*++&*:)"{~@i:@+:

Try it online!

Based on JungHwan Min's method.

Explanation

[:+/@,*:>:(*++&*:)"{~@i:@+:  Input: n
                         +:  Double
                      i:     Range [-2n .. 2n]
                  "{~        For each pair (x, y)
                *:             Square both x and y
              +                Add x^2 and y^2
             +                 Plus
            *                  Product of x and y
        >:                   Less than or equal to
      *:                     Square of n
     ,                       Flatten
  +/                         Reduce by addition

Answer 7

APL (Dyalog Classic), 23 bytes

{1+6×+/-/⌊⍵÷1+3⊥¨⍳⍵2}×⍨

Try it online!

tribute to xnor's and lynn's answers

the last test is commented because it needs more memory, e.g. MAXWS=200M in the env

Answer 8

Jelly,  15  13 bytes

-2 thanks to Dennis (just increment the square to avoid concatenation of a zero; avoid head by using a post-difference modulo-slice rather than a pre-difference slice)

^{Uses the "black magic" method of honing in on the answer that was exposed by xnor in their Python answer, but uses iteration rather than recursion (and a little less calculation)}

²:Ѐ‘$Im3S×6C

A monadic link accepting a non-negative integer and returning a positive integer.

Try it online! Or see the test-suite.

How?

²:Ѐ‘$Im3S×6C - Main Link: non-negative integer, n     e.g. 7
²             - square                                     49
     $        - last two links as a monad:
    ‘         -   increment                                50
  Ѐ          -   map across (implicit range of) right with:
 :            -     integer division                       [49,24,16,12,9,8,7,6,5,4,4,4,3,3,3,3,2,2,2,2,2,2,2,2,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,0]
      I       - incremental differences                    [-25,-8,-4,-3,-1,-1,-1,-1,-1,0,0,-1,0,0,0,-1,0,0,0,0,0,0,0,-1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,-1]
       m3     - every third element                        [-25,-3,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,-1]
         S    - sum (vectorises)                           -31
          ×6  - multiply by six                           -186
            C - complement (1-X)                           187

Answer 9

Jelly, 14 bytes

ḤŒR+²_×ʋþ`F½»ċ

Uses @JungHwanMin's method.

Try it online!

Answer 10

JavaScript (ES6), 65 bytes

This is a port of @JungHwanMin's solution.

f=(n,y=x=w=n*2)=>y-~w&&(x*x+x*y+y*y<=n*n)+f(n,y-=--x<-w&&(x=w,1))

Try it online!

---

Original answer (ES7), 70 bytes

Simply walks through the grid and counts the matching points.

f=(n,y=x=n*=2)=>y+n+2&&(x*x*3+(y-x%2)**2<=n*n)+f(n,y-=--x<-n&&(x=n,2))

Try it online!

Answer 11

Java 8, 65 bytes

n->f(n,1)int f(int n,int a){return n*n<a/3?1:n*n/a*6-f(n,a+a%3);}

Port of @xnor's Python 2 answer.

Try it online.

Answer 12

Pari/GP, 42 bytes

Using the built-in qfrep.

n->1+2*vecsum(Vec(qfrep([2,1;1,2],n^2,1)))

qfrep(q,B,{flag=0}): vector of (half) the number of vectors of norms from 1 to B for the integral and definite quadratic form q. If flag is 1, count vectors of even norm from 1 to 2B.

Try it online!

Answer 13

Wolfram Language (Mathematica), 39 bytes

Length@Solve[x(x+y)+y^2<=#^2,Integers]&

Try it online!

Using JungHwan Min's coordinate transformation and simply counting the solutions over the integers.

Answer 14

C# (Visual C# Interactive Compiler), 68 bytes

n=>{int g(int x,int y)=>x*x<y/3?1:x*x/y*6-g(x,y+y%3);return g(n,1);}

Try it online!

Same as everyone else, unfortunately. I know there's probably a better way of writing this, but declaring and calling a lambda at the same time in c# is not exactly something I do, well, ever. Though in my defense, I can't think of a good reason (outside code golf, of course) to do so. Still, if someone knows how you can do this, let me know and/or steal the credit, I guess.

Answer 15

05AB1E, 15 bytes

nD>L÷¥ā3%ÏO6*±Ì

Port of @JonathanAllans Jelly answer, which in turn is a derivative from @xnor's 'black magic' formula.

Try it online or verify all test cases.

Explanation:

n                # Square the (implicit) input-integer
 D>              # Duplicate it, and increase the copy by 1
   L             # Create a list in the range [1, input^2+1]
    ÷            # Integer divide input^2 by each of these integers
     ¥           # Take the deltas
      ā          # Push a list in the range [1, length] without popping the deltas itself
       3%        # Modulo each by 3
         Ï       # Only leave the values at the truthy (==1) indices
          O      # Take the sum of this list
           6*    # Multiply it by 6
             ±   # Take the bitwise NOT (-n-1)
              Ì  # And increase it by 2
                 # (after which the result is output implicitly)