1
2
Introduction
We know that the factorial notation is valid for all natural numbers. However, Euler had extended it for all positive real numbers, as well as for complex numbers by defining a function, which is known as the Gamma Function. It is represented by Γ.
Challenge
You will be given a non-negative floating point number, say 'n' (with a maximum of 2 decimal places in it), and you need to output the factorial of that number correct to at least 3 decimal places. Assume all inputs to be valid, and n <= 7.
Now talking about Gamma function, there is an integral which can be used to find the value of any factorial. You may choose to use it. You can find more information here. The Gamma function is recursive in nature. One important property, which would probably be useful to you is:
Γ(n) = (n-1)! , which means that, n! = Γ(n) . n
Also note that we really do not need to know Γ(n) for all values of n. For instance, look at the number 4.5 - we can write its factorial as:
4.5! = 4.5 * 3.5 * 2.5 * 1.5 * 0.5! = 59.0625 * 0.5!
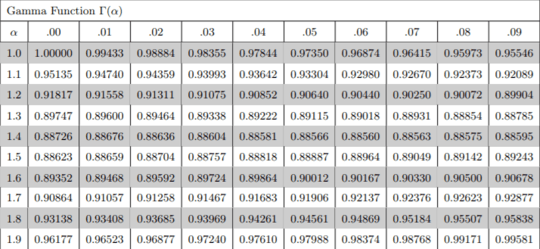
So here we need only the value of 0.5! , which means the value of Γ(1.5). Also, similarly, we can find the factorial of any decimal if we know the values of factorials of numbers between 0 and 1, i.e, values of gamma function of numbers between 1 and 2. You need it, so that is why there is a table below for your help:
Using this table, we can see that 0.5!, i.e, the value of Γ(1.5) = 0.88623, which gives our result: (4.5)! = 59.0625 * 0.88623 = 52.3429594 , which is indeed a good result. Similarly,
(5.7)! = (5.7)*(4.7)*(3.7)*(2.7)*(1.7)*(0.7)! = 454.97457 * 0.90864 = 413.408093
Also, if you do not wish to use the table for calculating the gamma function, here is a simple integral to help you out:
Remember that you can provide your answers only up to 3 decimal places if you want to. But the value should have minimum error. Like, +- 0.003 is acceptable.
You are free to decide in what way you want to compute the factorial - whether by the integral, or by the table, or using any other method.
Examples
Please note that here the answer is correct to 3 decimal places.
2.4 -> 2.981
3.9 -> 20.667
2.59 -> 3.675
1.7 -> 1.545
0.5 -> 0.886
Scoring
This is code-golf, so the shortest code wins!
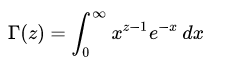
Please note that this challenge was posted on sandbox and people decided that this is not a dupe because this challenge allows built ins. – Manish Kundu – 2018-03-06T16:07:29.443
Can we output as a rational number (i.e fraction)? Like,
8275608925237915/2251799813685248for the 3rd test case. – Mr. Xcoder – 2018-03-06T16:48:52.007Sorry but as per the rules, decimal answers only – Manish Kundu – 2018-03-06T16:50:21.460
I interpreted "3 decimal places" to mean the leading digits, so "the relative error is
< 1/1000". But your examples seems to imply 3 digits after the decimal point, which would be a relative error of1/5040000for7!which is more accurate than your table. You can almost see this in your example of5.7!where the correct result413.40752only juuust rounds to413.408. It should be easy to find examples where it fails. Please clarify what you mean – Ton Hospel – 2018-03-06T17:27:07.453@TonHospel well I meant 3 places after decimal.Also the table is very unlikely to fail. – Manish Kundu – 2018-03-06T17:36:42.257
Aww, I was about to extend Whispers' factorial notation to cover the gamma function, and it'll look like cheating if I add an answer now. – caird coinheringaahing – 2018-03-06T18:54:10.837
4Since all built-in solutions are being combined in a single post, I consider this a duplicate of the Gamma challenge. – Dennis – 2018-03-06T18:54:19.473
1I think that near
7!the table is actually very likely to fail for 3 digits after.. And even if it didn't, you don't want to have to think about1000.000499vs1000.000501so you should really have asked for accuracy as a max absolute error – Ton Hospel – 2018-03-06T19:21:20.497At least you could have agreed upon this being a duplicate in the sandbox itself! What a waste of time. – Manish Kundu – 2018-03-07T08:21:20.547