Sparse Protractor

Question

Given some positive integer n, design a protractor with the fewest number of marks that lets you measure all angles that are an integral multiple of 2π/n (each in a single measurement).

Details

As an output, you may output a list of integers in the range 0 to n-1 (or 1 to n) that represent the position of each mark. Alternatively you can output a string/list of length n with a # at the position of each mark and a _ (underscore) where there is none. (Or two different characters if more convenient.)
Example: For n = 5 you need exactly 3 marks to be able to measure all angles 2π/5, 4π/5, 6π/5, 8π/5, 2π by setting (for example) one mark at 0, one mark at 2π/5 and one mark at 6π/5. We can encode this as a list [0,1,3] or as a string ##_#_.

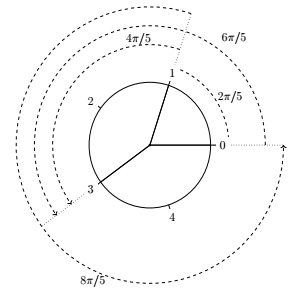
Examples

Note that the outputs are not necessarily unique.

n:  output:
 1  [0]
 2  [0,1]
 3  [0,1]
 4  [0,1,2]
 5  [0,1,2]
 6  [0,1,3]
 7  [0,1,3]
 8  [0,1,2,4]
 9  [0,1,3,4]
10  [0,1,3,6]
11  [0,1,3,8]
20  [0,1,2,3,6,10]

PS: This is similar to the sparse ruler problem, but instead of a linear scale (with two ends) we consider a circular (angular) scale.

PPS: This script should compute one example of a set of marks for each n. Try it online!

PPPS: As @ngn pointed out, this problem is equivalent to finding a minimal difference base of a cyclic group of order n. The minimal orders are listed in http://oeis.org/A283297 and some theoretical bounds are found in https://arxiv.org/pdf/1702.02631.pdf

Answer 1

MATL, 20 bytes

:qGZ^!"G:q@&-G\m?@u.

This runs out of memory on TIO for inputs beyond 8.

Try it online!

How it works

This generates the Cartesian power of [0 1 ... n-1] with exponent n, and uses a loop to test each Cartesian tuple. The test consists in computing all pairwise differences of element if the tuple, and seeing if those differences modulo n include all numbers 0, 1, ..., n-1.

As soon as a Cartesian tuple fulfilling the condition is found the loop is exited, and the unique entries in that tuple are printed as the solution.

This works because given u > v, a sufficient set of tuples with u unique entries are guaranteed to be tested earlier than any tuple with v unique entries. A "sufficient set" means that if none of the tuples in that set are a solution then no other tuple with the same number of unique entries is a solution.

For example, for n = 3 the Cartesian tuples are as shown below, where each row is a tuple:

0 0 0
0 0 1
0 0 2
0 1 0
0 1 1
0 1 2
0 2 0
 ···
2 2 1
2 2 2

• The first tuple, 0 0 0, is the only relevant tuple with 1 unique value. Even if 1 1 1 and 2 2 2 will appear much later, 0 0 0 is a solution if and only if those are. So the singleton set formed by the tuple 0 0 0 is a sufficient set for u = 1.
• The second and third tuples, namely 0 0 1and 0 0 2, form a sufficient set for u = 2; that is, they cover all cases with 2 unique values. The fourth tuple, 0 1 0, will never be selected as solution, because 0 0 1 will have been tested first. Similarly, the tuple 0 2 0 will never be selected because it appears later than 0 0 2. Tuples such as 2 2 1 will never be selected as solution because the 0 0 1 is equivalent (modulo n and up to duplicated values) and appears first.
• Etc.

Commented code:

:q         % Push [0 1 ... n-1], where n is the input (implicit)
GZ^        % Cartesian power with exponent n. Gives an (n^n) × n matrix
           % where each row is a Cartesian tuple
!          % Transpose. Now each Cartesian tuple is a column
!"         % For each column (that is, each Cartesian tuple)
  G:q      %   Push [0 1 ... n-1] (*)
  @        %   Push current column
  &-       %   Matrix of pairwise differences (**)
  G\       %   Modulo n, element-wise
  m        %   Ismember function: for each entry in (*), gives true iff
           %   it is present in (**)
  ?        %   If all entries are true
    @      %     Push current column
    u      %     Unique entries. This is the solution
    .      %     Break loop
           %   End (implicit)
           % End (implicit)
           % Display (implicit)

Answer 2

Jelly, 13 bytes

ŒPðṗ2I%QLðÐṀḢ

Try it online!

How it works

ŒPðṗ2I%QLðÐṀḢ  Main link. Argument: n (integer)

ŒP             Powerset; generate all subsequences of [1, ..., n].
  ð       ÐṀ   Begin a dyadic chain. Call it with all subsequences S as left
               argument and n as right one. Return the array of all sequences for
               which the chain returns the maximal result, i.e., [0, ..., n-1].
   ṗ2              Cartesian power 2; generate all pairs of elements of S.
     I             Increments; map each pair [x, y] to [y-x].
      %            Map each [y-x] to [(y-x)%n].
       Q           Unique; deduplicate the array of modular difference singletons.
        L          Take the length.
         ð     Begin a new, dyadic chain.
               Left argument: S' (filted subsequences). Right argument: n
            Ḣ  Take the first element of S'.
               Since S was sorted by length, so is S', so the first element of S'
               is the shortest subsequence that satisfies the condition.

Answer 3

Stax, 26 21 bytes

Åæ4&╕u◙╩►s∙Φ▬═(0~ d+Q

Run and debug online!

Right now the online version fails for input 20 but this bug has been fixed and is yet to be deployed to the online interpreter Deployed. Beware it takes some time to run the 20 case.

Explanation

Turns out that due to way pairwise difference is calculated, I don't need to worry about the equivalence of k and x-k here. Saving 5 bytes.

Uses the unpacked version to explain.

rS{%o~{;i@c:2{E-x%mu%x<wm
r                            [0..`x`], where `x` is input
 S                           Powerset
  {%o~                       Sort by length
      {;i@             w     For each element in the powerset
          c:2                All pairs
             {    m          Map each pair `[p,q] to
              E-                 `q-p`
                x%               `(q-p)%x`
                   u%        Count of unique modulo differences
                     x<      Loop until the count of unique modulo differences is larger than the input(`n`)
                             Now we have found a valid set in the powerset
                        m    Output the members of the set,one element per line.

By enforcing the requirement that 0 and 1 both be members of the answer, we can generate the powerset with [2..x] instead of [0..x] and then add the 0 and 1 manually to every element in the powerset. It is more efficient but need to handle the input 1 specially and costs more bytes.

Answer 4

Jelly, 17 bytes

_þ¹F%³³Ḷ¤ḟ
ŒPÇÐḟḢ

Try it online!

-1 byte thanks to Mr. Xcoder

Answer 5

Python 2, 148 bytes

from itertools import*
def f(n):
 r=range(n)
 for i in r:
  for p in combinations(r,i+1):
   if all(any((y+x)%n in p for y in p)for x in r):return p

Try it online!