33
2
Apparently yes! In three easy steps.
Step 1
Let f(n) denote the prime-counting function (number of primes less than or equal to n).
Define the integer sequence s(n) as follows. For each positive integer n,
- Initiallize t to n.
- As long as t is neither prime nor 1, replace t by f(t) and iterate.
- The number of iterations is s(n).
The iterative process is guaranteed to end because f(n) < n for all n.
Consider for example n=25. We initiallize t = 25. Since this is not a prime nor 1, we compute f(25), which is 9. This becomes the new value for t. This is not a prime nor 1, so we continue: f(9) is 4. We continue again: f(4) is 2. Since this is a prime we stop here. We have done 3 iterations (from 25 to 9, then to 4, then to 2). Thus s(25) is 3.
The first 40 terms of the sequence are as follows. The sequence is not in OEIS.
0 0 0 1 0 1 0 2 2 2 0 1 0 2 2 2 0 1 0 3 3 3 0 3 3 3 3 3 0 3 0 1 1 1 1 1 0 2 2 2
Step 2
Given an odd positive integer N, build an N×N array (matrix) by winding the finite sequence s(1), s(2), ..., s(N2) to form a square outward spiral. For example, given N = 5 the spiral is
s(21) s(22) s(23) s(24) s(25)
s(20) s(7) s(8) s(9) s(10)
s(19) s(6) s(1) s(2) s(11)
s(18) s(5) s(4) s(3) s(12)
s(17) s(16) s(15) s(14) s(13)
or, substituting the values,
3 3 0 3 3
3 0 2 2 2
0 1 0 0 0
1 0 1 0 1
0 2 2 2 0
Step 3
Represent the N×N array as an image with a grey colour map, or with some other colour map of your taste. The map should be gradual, so that the order of numbers corresponds to some visually obvious order of the colours. The test cases below show some example colour maps.
The challenge
Given an odd positive integer N, produce the image described above.
Rules
The spiral must be outward, but can be clockwise or counter-clockwise, and can start moving right (as in the above example), left, down or up.
The scales of the horizontal and vertical axes need not be the same. Also axis labels, colorbar and similar elements are optional. As long as the spiral can be clearly seen, the image is valid.
Images can be output by any of the standard means. In particular, the image may be displayed on screen, or a graphics file may be produced, or an array of RGB values may be output. If outputting a file or an array, please post an example of what it looks like when displayed.
Input means and format are flexible as usual. A program or a function can be provided. Standard loopholes are forbidden.
Shortest code in bytes wins.
Test cases
The following images (click for full resolution) correspond to several values of N. A clock-wise, rightward-first spiral is used, as in the example above. The images also illustrate several valid colour maps.
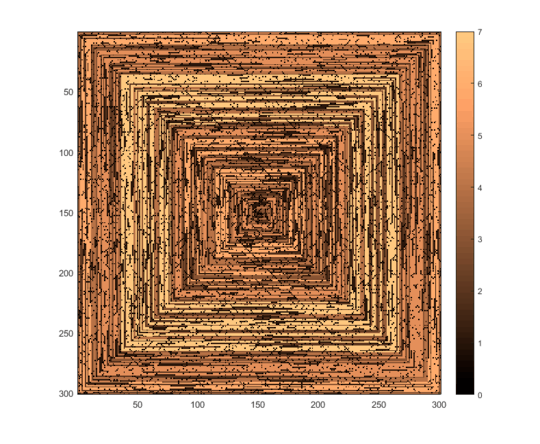
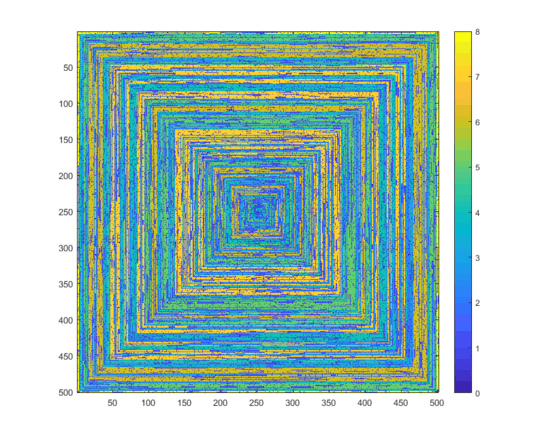
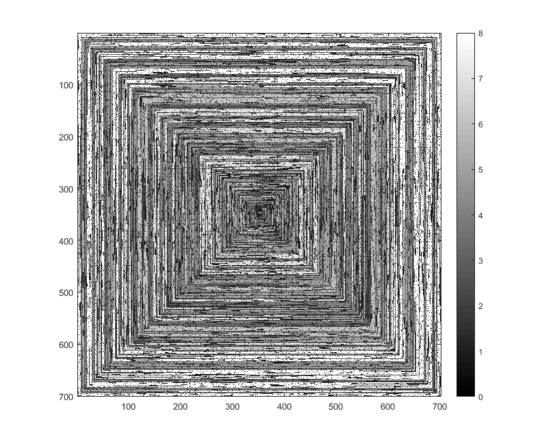




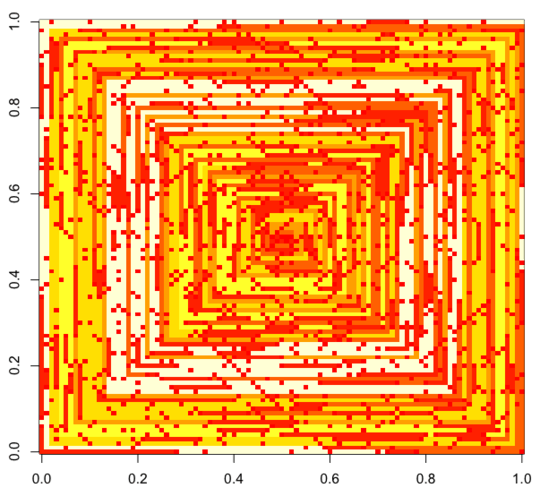
If an array of values of
s(n)can be fed into some plotting function/package without being modified (I thinkimshowin matplotlib could handle this for example) is this an acceptable output form? – dylnan – 2018-01-30T21:39:39.030@dylnan Sure, as long as it plots the image on screen or produces a file it's valid. In fact I generated the examples with something similar to what you mention. Just be careful with the scaling of values. For example it's not acceptable if all values above 1 are given the same color, as Matlab's (and possibly Matplotlib's)
imshowdoes – Luis Mendo – 2018-01-30T21:43:47.990good point. Not sure if
imshowdoes that. – dylnan – 2018-01-30T21:45:53.897i am so confused. What is going on? – Christopher – 2018-01-31T03:26:01.577
@Christopher Is there anything in the challenge I should clarify? – Luis Mendo – 2018-01-31T10:05:12.743
Related to spiral. – user202729 – 2018-01-31T10:29:25.047
Related -- prime counting function – Giuseppe – 2018-01-31T12:26:36.123
How did you come up with this challenge? – kamoroso94 – 2018-01-31T14:24:47.930
1
@kamoroso94 Please see here
– Luis Mendo – 2018-01-31T14:46:33.127@LuisMendo I just don't understand how step one works at all. I find the notation confusing,"iteratively replace t by f(t) until the result is either prime or 1." is the hardest part – Christopher – 2018-01-31T15:19:55.420
@Christopher I have changed that phrase and explained the example step by step. Clearer now? – Luis Mendo – 2018-01-31T15:32:08.890
1Yeah very clear – Christopher – 2018-01-31T16:12:02.353