13
2
This challenge is from an admission test to a closed number cyber security course. Anyway it doesn't have to do with cyber security, it's just to test the students logical and coding skills.
Task
Write a program that removes entries from an array so that the remaining values are sorted in a strictly decreasing order and their sum is the maximized among all other possible decreasing sequences.
Input and Output
Input will be an array of integer values strictly greater than 0 and all different from each other.
You are free to choose whether to read input from file, command line or stdin.
Output will be a descending-sorted subarray of the input one, whose sum is greater than any other possible descending-sorted subarray.
Note: [5, 4, 3, 2] is a subarray of [5, 4, 1, 3, 2], even if 4 and 3 are not adjacent. Just because the 1 was popped.
Bruteforce solution
The simplest solution of course would be iterate among all possible combinations of the given array and search for a sorted one with the greatest sum, that would be, in Python:
import itertools
def best_sum_desc_subarray(ary):
best_sum_so_far = 0
best_subarray_so_far = []
for k in range(1, len(ary)):
for comb in itertools.combinations(ary, k):
if sum(comb) > best_sum_so_far and all(comb[j] > comb[j+1] for j in range(len(comb)-1)):
best_subarray_so_far = list(comb)
best_sum_so_far = sum(comb)
return best_subarray_so_far
Unfortunately, since checking if the array is sorted, and calculating the sum of it's elements is 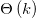
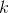
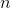
Challenge
Your goal is to achieve a better time complexity than the bruteforce above. The solution with the smallest asymptotic time complexity is the winner of the challenge. If two solutions have the same asymptotic time complexity, the winner will be the one with the smallest asymptotic spatial complexity.
Note: You can consider reading, writing and comparing atomic even on large numbers.
Note: If there are two or more solutions return either of them.
Test cases
Input: [200, 100, 400]
Output: [400]
Input: [4, 3, 2, 1, 5]
Output: [4, 3, 2, 1]
Input: [50, 40, 30, 20, 10]
Output: [50, 40, 30, 20, 10]
Input: [389, 207, 155, 300, 299, 170, 158, 65]
Output: [389, 300, 299, 170, 158, 65]
Input: [19, 20, 2, 18, 13, 14, 8, 9, 4, 6, 16, 1, 15, 12, 3, 7, 17, 5, 10, 11]
Output: [20, 18, 16, 15, 12, 7, 5]
Input: [14, 12, 24, 21, 6, 10, 19, 1, 5, 8, 17, 7, 9, 15, 23, 20, 25, 11, 13, 4, 3, 22, 18, 2, 16]
Output: [24, 21, 19, 17, 15, 13, 4, 3, 2]
Input: [25, 15, 3, 6, 24, 30, 23, 7, 1, 10, 16, 29, 12, 13, 22, 8, 17, 14, 20, 11, 9, 18, 28, 21, 26, 27, 4, 2, 19, 5]
Output: [25, 24, 23, 22, 17, 14, 11, 9, 4, 2]
Related. (I can't check right now whether the two algorithms are in fact equivalent, but I think they might be.) – Martin Ender – 2018-01-30T20:24:27.180
Comments are not for extended discussion; this conversation has been moved to chat.
– Martin Ender – 2018-02-20T08:41:07.900