I want my book to be away from this table

Question

Story

So I have a book that I want to separate from my table with nothing but other books. I want to know how many books do I need to achieve this with \$n\$ book lengths.

Here's a visualization that my friend at Wolfram drew for me:

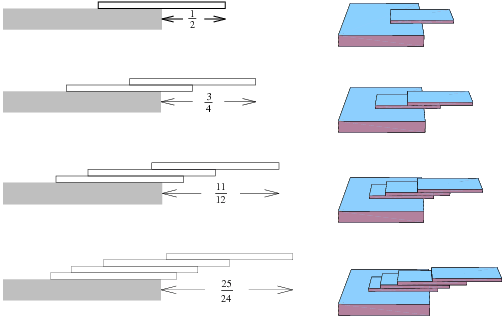
More information about the topic in Wolfram and Wikipedia.

Challenge

Given an integer input \$n\$, output how many books needed for the top book to be \$n\$ book length away from the table horizontally.
or
Find the smallest integer value of \$m\$ for input \$n\$ in the following inequality. $$\sum_{i=1}^{m}\frac{1}{2i} \geq n$$

Edit: for fractions use at least a IEEE single-precision floating point. _{sorry for editing challenge after posting}

_{(OEIS A014537)}

Test cases

 1          4
 2         31
 3        227
 5      12367
10  272400600

Answer 1

Octave, 41 40 33 bytes

1 byte saved thanks to @Dennis

@(n)find(cumsum(.5./(1:9^n))>n,1)

Try it online!

Explanation

This uses the fact that harmonic numbers can be lower-bounded by a logarithmic function.

Also, the >= comparison can be replaced by > because harmonic numbers cannot be even integers (thanks, @Dennis!).

@(n)                                   % Anonymous function of n
                     1:9^n             % Range [1 2 ... 9^n]
                .5./(     )            % Divide .5 by each entry
         cumsum(           )           % Cumulative sum
                            >n         % Is each entry greater than n?
    find(                     ,1)      % Index of first true entry

Answer 2

Python 3, 35 bytes

f=lambda n,k=2:n>0and-~f(n-1/k,k+2)

Try it online!

Answer 3

Husk, 8 bytes

V≥⁰∫m\İ0

Try it online!

Since Husk uses rational numbers when it can, this has no floating point issues

Explanation

      İ0    The infinite list of positive even numbers
    m\      Reciprocate each
   ∫        Get the cumulative sum
V           Find the index of the first element
 ≥⁰         that is greater than or equal to the input

Answer 4

JavaScript, 30 bytes

A recursive function so it'll crap out pretty early.

f=(n,x=0)=>n>0?f(n-.5/++x,x):x

Try it online

Answer 5

Haskell, 38 bytes

k!n|n<=0=0|x<-n-1/(2*k)=1+(k+1)!x
(1!)

Answer 6

Javascript (ES6), 34 bytes

n=>eval("for(i=0;n>0;n-=.5/i)++i")

Ungolfed

n => {
    for(i = 0; n > 0; ++i)
        n -= .5 / i
    return i;
}

Test Cases

f=n=>eval("for(i=0;n>0;n-=.5/i)++i")

<button onclick="console.log(f(1))">Run for n = 1</button>
<button onclick="console.log(f(2))">Run for n = 2</button>
<button onclick="console.log(f(3))">Run for n = 3</button>
<button onclick="console.log(f(5))">Run for n = 5</button>
<button onclick="console.log(f(10))">Run for n = 10</button>

Answer 7

Swift, 65 bytes

func f(n:Double){var i=0.0,s=i;while s<n{i+=1;s+=0.5/i};print(i)}

Try it online!

Ungolfed

func f(n:Double) {
  var i = 0.0, s = 0.0
  while s < n {
    i += 1;
    s += 0.5 / i
  }
  print(i)
}

Answer 8

R, 39 bytes

function(n){while((F=F+.5/T)<n)T=T+1;T}

Try it online!

Brute Force!

Answer 9

Jelly, 8 bytes

RİSH:ð1#

This is very slow.

Try it online!

Answer 10

Haskell, 71 49 48 bytes

f x=length.fst.span(<x).scanl(+)0$(0.5/)<$>[1..]

@BMO saved me a whopping 22 bytes!

Answer 11

Julia 0.6, 30 27 bytes

<(n,i=1)=n>0?n-.5/i<i+1:i-1

Try it online!

Only works up to n = 6, because Julia has no tail call optimization.

-3 bytes thanks to Dennis.

Answer 12

TI-BASIC, 27 bytes

Prompts user for input and displays output on termination. Note: ⁻¹ is the ^-1 (inverse) token.

Input N
1
Repeat 2N≤Σ(I⁻¹,I,1,Ans
Ans+1
End
Ans

Answer 13

Japt, 12 bytes

The same length as, but slightly more efficient than, the recursive option.

@T¨(Uµ½÷X}a1

Try it

---

Explanation

@T¨(Uµ½÷X}a1
                 :Implicit input of integer U
@        }a1     :Return the first number X >=1 that returns truthy when passed through the following function
 T               :Zero
  ¨              :Greater than or equal to
    Uµ           :Decrement U by...
      ½÷X        :0.5 divided by X

Answer 14

05AB1E, 11 bytes

XµN·zODI›}N

Try it online!

Explanation

Xµ       }    # loop until counter is 1
  N·z         # push 1/(2*N)
     O        # sum the stack
      DI›     # break if the sum is greater than the input
          N   # push N

Answer 15

Pyth, 10 bytes

f!>Qsmc1yh

Try it online!

Extremely slow.

Pyth, 10 bytes

fgscL1STyQ

Try it online!

Answer 16

J, 22 bytes

-6 bytes thanks to frownyfrog

I.~0+/\@,1%2*1+[:i.9&^

Try it online!

original answer

Luis's answer in J:

1+]i.~[:<.[:+/\1%2*1+[:i.9&^

Ungolfed

1 + ] i.~ [: <. [: +/\ 1 % 2 * 1 + [: i. 9&^

Mostly curious to see if it can be drastically improved (cough paging miles)

Explanation

1 +      NB. 1 plus... 
] i.~    NB. find the index of the arg in...
[: <.    NB. the floor of...
[: +/\   NB. the sumscan of...
1 %      NB. the reciprical of...
2 *      NB. two times...
1 +      NB. 1 plus...
[: i.    NB.  the integers up to 
9&^      NB. 9 raised to the power of the arg

Try it online!

Answer 17

PHP, 35 bytes

while($argv[1]>$s+=.5/++$i);echo$i;

Run it using the CLI:

$ php -d error_reporting=0 -r 'while($argv[1]>$s+=.5/++$i);echo$i;' 5

Answer 18

Wolfram Language (Mathematica), 40 bytes

⌈x/.NSolve[HarmonicNumber@x==2#,x]⌉&

Try it online!

Answer 19

Java 8, 49 bytes

n->{float r=0,s=0;for(;s<n;)s+=.5f/++r;return r;}

Explanation:

Try it online. (Times out for test cases above n=7.)

n->{             // Method with integer parameter and float return-type
  float r=0,     //  Result-float, starting at 0
        s=0;     //  Sum-float, starting at 0
  for(;s<n;)     //  Loop as long as the sum is smaller than the input
    s+=.5f/++r;  //   Increase the sum by `0.5/(r+1)`,
                 //   by first increasing `r` by 1 with `r++`
  return r;}     //  Return the result-float

Answer 20

tinylisp, 98 bytes

(load library
(d _(q((k # N D)(i(l N(* D # 2))(_(inc k)#(+(* N k)D)(* D k))(dec k
(q((#)(_ 1 # 0 1

The last line is an unnamed lambda function that takes the number of book-lengths and returns the number of books needed. Try it online!

Explanation

The only numeric data type tinylisp has is integers, so we calculate the harmonic series as a fraction by keeping track of the numerator and denominator. At each step, N is the numerator, D is the denominator, and k is the sum index. We want the new partial sum to be N/D + 1/k, or (N*k + D)/(D*k). Thus, we recurse with a new numerator of N*K + D, a new denominator of D*k, and a new index of k+1.

The recursion should halt once the partial sum is greater than or equal to #, the desired number of book-lengths. At this point, we've gone one book too far, so we return k-1. The condition is 1/2 * N/D < #; multiplying out the denominator, we get N < D*#*2, which is the golfiest way to write it.

The recursive helper function _ does all these calculations; the main function is merely a one-argument wrapper that calls _ with the correct starting values for k, N, and D.