​L​o​o​p​ ​I​t​

Question

Note: The title of this question should be "Loop It", but because title needs to be at least 15 characters, there are some invisible spaces. This note is such that the challenge can be searched for.

---

Challenge

Given a finite list of unique integral points in the plane, find a polygon whose vertices are exactly those points, which does not self intersect.

Details

• As input you can take e.g. two lists with each the x- and y-coordinates or a list of pairs.
• The input list contains at least 3 points.
• Note that this means there is never a unique solution.
• The list of inputs is can be assumed to be not co-linear (the points cannot be contained in one line), this means there actually is such a non-self-intersecting polygon.
• The angles at each vertex is arbitrary, this includes 180°.
• For an input of length n, the output should be a permutation (p1,p2,p3,...,pn) of (1,2,3,...,n) where the k-th entry pk represents the p-th point in the input list. This means we have a line from p1 to p2, a line from p2 to p3 etc, as well as a line from pn to p1. (You can also use the 0-based indices.) Alternatively you can just output the list of input points in the right order.

Examples

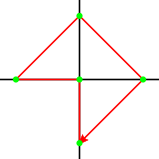
Let's say we have the points [(0,0),(0,1),(1,0),(-1,0),(0,-1)] and we want to represent following path:

This means we would output the list [5,1,4,2,3]

Here some more suggestion to try (I recommend looking at the corresponding plots to verify the goals.)

Triangle
[(0,0),(0,1),(1,0)]

S-Curve
[(0,0),(0,1),(0,2),(0,3),(0,4),(1,0),(2,0),(2,1),(2,2),(2,3),(2,4),(3,4),(4,0),(4,1),(4,2),(4,3),(4,4)]

L-Shape
[(4,0),(1,0),(3,0),(0,0),(2,0),(0,1)]

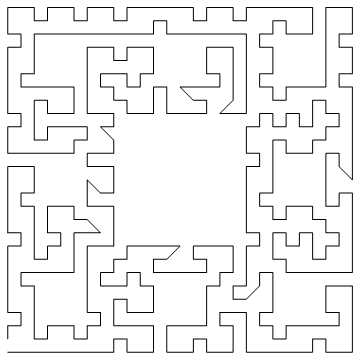
Menger Sponge
[(1,1),(2,1),(3,1),(4,1),(5,1),(6,1),(7,1),(8,1),(9,1),(10,1),(11,1),(12,1),(13,1),(14,1),(15,1),(16,1),(17,1),(18,1),(19,1),(20,1),(21,1),(22,1),(23,1),(24,1),(25,1),(26,1),(27,1),(1,2),(3,2),(4,2),(6,2),(7,2),(9,2),(10,2),(12,2),(13,2),(15,2),(16,2),(18,2),(19,2),(21,2),(22,2),(24,2),(25,2),(27,2),(1,3),(2,3),(3,3),(4,3),(5,3),(6,3),(7,3),(8,3),(9,3),(10,3),(11,3),(12,3),(13,3),(14,3),(15,3),(16,3),(17,3),(18,3),(19,3),(20,3),(21,3),(22,3),(23,3),(24,3),(25,3),(26,3),(27,3),(1,4),(2,4),(3,4),(7,4),(8,4),(9,4),(10,4),(11,4),(12,4),(16,4),(17,4),(18,4),(19,4),(20,4),(21,4),(25,4),(26,4),(27,4),(1,5),(3,5),(7,5),(9,5),(10,5),(12,5),(16,5),(18,5),(19,5),(21,5),(25,5),(27,5),(1,6),(2,6),(3,6),(7,6),(8,6),(9,6),(10,6),(11,6),(12,6),(16,6),(17,6),(18,6),(19,6),(20,6),(21,6),(25,6),(26,6),(27,6),(1,7),(2,7),(3,7),(4,7),(5,7),(6,7),(7,7),(8,7),(9,7),(10,7),(11,7),(12,7),(13,7),(14,7),(15,7),(16,7),(17,7),(18,7),(19,7),(20,7),(21,7),(22,7),(23,7),(24,7),(25,7),(26,7),(27,7),(1,8),(3,8),(4,8),(6,8),(7,8),(9,8),(10,8),(12,8),(13,8),(15,8),(16,8),(18,8),(19,8),(21,8),(22,8),(24,8),(25,8),(27,8),(1,9),(2,9),(3,9),(4,9),(5,9),(6,9),(7,9),(8,9),(9,9),(10,9),(11,9),(12,9),(13,9),(14,9),(15,9),(16,9),(17,9),(18,9),(19,9),(20,9),(21,9),(22,9),(23,9),(24,9),(25,9),(26,9),(27,9),(1,10),(2,10),(3,10),(4,10),(5,10),(6,10),(7,10),(8,10),(9,10),(19,10),(20,10),(21,10),(22,10),(23,10),(24,10),(25,10),(26,10),(27,10),(1,11),(3,11),(4,11),(6,11),(7,11),(9,11),(19,11),(21,11),(22,11),(24,11),(25,11),(27,11),(1,12),(2,12),(3,12),(4,12),(5,12),(6,12),(7,12),(8,12),(9,12),(19,12),(20,12),(21,12),(22,12),(23,12),(24,12),(25,12),(26,12),(27,12),(1,13),(2,13),(3,13),(7,13),(8,13),(9,13),(19,13),(20,13),(21,13),(25,13),(26,13),(27,13),(1,14),(3,14),(7,14),(9,14),(19,14),(21,14),(25,14),(27,14),(1,15),(2,15),(3,15),(7,15),(8,15),(9,15),(19,15),(20,15),(21,15),(25,15),(26,15),(27,15),(1,16),(2,16),(3,16),(4,16),(5,16),(6,16),(7,16),(8,16),(9,16),(19,16),(20,16),(21,16),(22,16),(23,16),(24,16),(25,16),(26,16),(27,16),(1,17),(3,17),(4,17),(6,17),(7,17),(9,17),(19,17),(21,17),(22,17),(24,17),(25,17),(27,17),(1,18),(2,18),(3,18),(4,18),(5,18),(6,18),(7,18),(8,18),(9,18),(19,18),(20,18),(21,18),(22,18),(23,18),(24,18),(25,18),(26,18),(27,18),(1,19),(2,19),(3,19),(4,19),(5,19),(6,19),(7,19),(8,19),(9,19),(10,19),(11,19),(12,19),(13,19),(14,19),(15,19),(16,19),(17,19),(18,19),(19,19),(20,19),(21,19),(22,19),(23,19),(24,19),(25,19),(26,19),(27,19),(1,20),(3,20),(4,20),(6,20),(7,20),(9,20),(10,20),(12,20),(13,20),(15,20),(16,20),(18,20),(19,20),(21,20),(22,20),(24,20),(25,20),(27,20),(1,21),(2,21),(3,21),(4,21),(5,21),(6,21),(7,21),(8,21),(9,21),(10,21),(11,21),(12,21),(13,21),(14,21),(15,21),(16,21),(17,21),(18,21),(19,21),(20,21),(21,21),(22,21),(23,21),(24,21),(25,21),(26,21),(27,21),(1,22),(2,22),(3,22),(7,22),(8,22),(9,22),(10,22),(11,22),(12,22),(16,22),(17,22),(18,22),(19,22),(20,22),(21,22),(25,22),(26,22),(27,22),(1,23),(3,23),(7,23),(9,23),(10,23),(12,23),(16,23),(18,23),(19,23),(21,23),(25,23),(27,23),(1,24),(2,24),(3,24),(7,24),(8,24),(9,24),(10,24),(11,24),(12,24),(16,24),(17,24),(18,24),(19,24),(20,24),(21,24),(25,24),(26,24),(27,24),(1,25),(2,25),(3,25),(4,25),(5,25),(6,25),(7,25),(8,25),(9,25),(10,25),(11,25),(12,25),(13,25),(14,25),(15,25),(16,25),(17,25),(18,25),(19,25),(20,25),(21,25),(22,25),(23,25),(24,25),(25,25),(26,25),(27,25),(1,26),(3,26),(4,26),(6,26),(7,26),(9,26),(10,26),(12,26),(13,26),(15,26),(16,26),(18,26),(19,26),(21,26),(22,26),(24,26),(25,26),(27,26),(1,27),(2,27),(3,27),(4,27),(5,27),(6,27),(7,27),(8,27),(9,27),(10,27),(11,27),(12,27),(13,27),(14,27),(15,27),(16,27),(17,27),(18,27),(19,27),(20,27),(21,27),(22,27),(23,27),(24,27),(25,27),(26,27),(27,27)]

Answer 1

Mathematica 29 28 Bytes

FindShortestTour (16 Bytes) does the trick but delivers some extraneous info not asked for (the path length, and a return to the starting point).

Most@*Last@*FindShortestTour

gives just the answer ( -1 byte thanks to @user202729 )

To visualize, use Graphics@Line[g[[%]]], where % is the permutation found above and g is the original point list.

Here is the visualization of the solution for the Menger Sponge:

Here is a solution on a 1000 random points:

The key here is knowing that the shortest tour or traveling salesman problem solution will never yield intersections when Euclidean distance is used as the metric. One of the steps to localize a solution and ensure optimality is to remove such intersections.

Answer 2

JavaScript (ES6), 365 341 bytes

Without any built-in, this turned out to be much longer than I expected. Many bytes are spent detecting collinear overlapping segments.

Takes input as an array of [x,y] coordinates. Returns a permutation of the input.

f=(a,p=[],o=([p,P],[q,Q],[r,R])=>Math.sign((S=[(p>q?r<q|r>p:r<p|r>q)|(P>Q?R<Q|R>P:R<P|R>Q),...S],Q-P)*(r-q)-(q-p)*(R-Q)))=>[...p,p[0]].some((A,i,P)=>P.some((C,j)=>j>i+1&&P[++j+!i]&&[E=o(A,B=P[i+1],C,S=[]),F=o(A,B,D=P[j]),G=o(C,D,A),H=o(C,D,B)].some(v=>!v&!S.pop())|E!=F&G!=H))?0:a[0]?a.some((_,i)=>r=f(b=[...a],p.concat(b.splice(i,1))))&&r:p

Demo

This snippet logs the output and draws the corresponding path in a canvas.

f=(a,p=[],o=([p,P],[q,Q],[r,R])=>Math.sign((S=[(p>q?r<q|r>p:r<p|r>q)|(P>Q?R<Q|R>P:R<P|R>Q),...S],Q-P)*(r-q)-(q-p)*(R-Q)))=>[...p,p[0]].some((A,i,P)=>P.some((C,j)=>j>i+1&&P[++j+!i]&&[E=o(A,B=P[i+1],C,S=[]),F=o(A,B,D=P[j]),G=o(C,D,A),H=o(C,D,B)].some(v=>!v&!S.pop())|E!=F&G!=H))?0:a[0]?a.some((_,i)=>r=f(b=[...a],p.concat(b.splice(i,1))))&&r:p

draw(f([[0,0],[0,1],[1,0]]), 1, 1)
draw(f([[0,0],[0,1],[1,0],[-1,0],[0,-1]]), 61, 21)
draw(f([[4,0],[1,0],[3,0],[0,0],[2,0],[0,1]]), 101, 1)

function draw(a, dx, dy) {
  console.log(JSON.stringify(a));

  ctx = C.getContext('2d');
  ctx.beginPath();
  [...a, a[0]].forEach(p => ctx.lineTo(p[0] * 20 + dx, p[1] * 20 + dy));
  ctx.stroke();
}

<canvas id=C></canvas>

How?

Here is the structure of the main recursive function f(), leaving aside the intersection testing code for now:

f = (a, p = []) =>                    // a = array of points, p = current path
  [...p,                              // build a closed path array P[] by adding the first
         p[0]]                        // point at the end of p[]
  .some((A, i, P) =>                  // for each point A at position i in P:
    P.some((C, j) =>                  //   for each point C at position j in P:
      j > i + 1 &&                    //     test whether C is at least 2 positions after A
      P[++j +                         //     and C is not the last point
              !i] &&                  //     and i > 0 or C is not the penultimate point
      intersection(                   //     and there's an intersection between
        A, P[i + 1], C, P[j]          //     the segments (A, P[i + 1]) and (C, P[j + 1])
      )                               //     (j was incremented above)
    )                                 //   end of inner some()
  ) ?                                 // end of outer some(); if truthy:
    0                                 //   discard this path by stopping recursion
  :                                   // else:
    a[0] ?                            //   if there's at least one remaining point:
      a.some((_, i) =>                //     for each remaining point at position i:
        r = f(                        //       do a recursive call with:
          b = [...a],                 //         a copy b[] of a[] without a[i] and
          p.concat(b.splice(i, 1)))   //         the extracted point added to the path
      ) && r                          //     end of some(); return the result, if any
    :                                 //   else:
      p                               //     this is a valid path: return it

Below is the detail of the intersection() test. This page provides a comprehensive explanation about the algorithm used.

[                                     // build an array containing:
  E = o(A, B = P[i + 1], C, S = []),  //   E = test of (A, B, C) (+ initialization of S[])
  F = o(A, B, D = P[j]),              //   F = test of (A, B, D)
  G = o(C, D, A),                     //   G = test of (C, D, A)
  H = o(C, D, B)                      //   H = test of (C, D, B)
]                                     //
.some(v =>                            // the segments are collinear and overlapping if:
  !v &                                //   any value above is 0
  !S.pop()                            //   and the corresponding entry in S[] is falsy
) |                                   // the segments intersect if:
E != F & G != H                       //   E is not equal to F and G is not equal to H

Finally, here is the definition of the helper function o():

o = (                                             // given three points represented by
  [p, P], [q, Q], [r, R]                          // a lowercase letter for x
) =>                                              // and an uppercase letter for y:
  Math.sign(                                      //
    (                                             //   1) prepend to the array S[]
      S = [                                       //      a boolean which is true if the
        (p > q ? r < q | r > p : r < p | r > q) | //      segment (P, Q) would not contain
        (P > Q ? R < Q | R > P : R < P | R > Q),  //      the point R, assuming that the
        ...S                                      //      3 points are collinear
      ],                                          //
                                                  //   2) return the orientation of P, Q, R:
      Q - P                                       //        -1 = counterclockwise
    ) * (r - q) - (q - p) * (R - Q)               //         0 = collinear
  )                                               //        +1 = clockwise

Answer 3

APL (Dyalog Classic), 42 38 bytes

{⍋(⍪,(|z)ׯ1*⊢=⌈/)12○z←0j1⊥¨⍵-⍵[⊃⍋↑⍵]}

Try it online!

Input is a list of coordinate pairs. Output is a 0-based permutation.

⍵ is the list of points - the argument to { }

⍵[⊃⍋↑⍵] is the leftmost-lowest point

⍵- translates all points so that leftmost-lowest is at the origin of the coordinate system

0j1 the imaginary unit i=sqrt(-1)

0j1⊥¨ decodes the coordinates as if digits in a base-i number system - i.e. turns (x,y) into a complex number ix+y

z← assign to z

12○ computes the complex numbers' arguments, a.k.a. theta angles, or APL circular function 12

(⍪,(|z)ׯ1*⊢=⌈/) is a train that computes a boolean mask of where the angles are at a maximum (⊢=⌈/), turns the 0 1 in the mask into 1 ¯1 by raising ¯1 to the corresponding power (¯1*), multiplies by the magnitudes of the complex numbers |z, and concatenates that to the right (,) of a tall thin 1-column matrix (⍪) of the angles.

⍋ grade - returns the permutation that would sort the rows of the matrix lexicographically in ascending order