19
2
Note: this challenge has been posted on the sandbox.
Introduction
This challenge is inspired by 2009 Putnam B1, a problem in an undergraduate mathematics competition. The problem is as follows:
Show that every positive rational number can be written as a quotient of products of factorials of (not necessarily distinct) primes. For example,
Challenge
Your challenge is to take a pair of relatively prime positive integers, representing the numerator and denominator of a positive rational number (or just the rational number itself) as input, and output two lists (or arrays, etc.) of prime numbers so that the inputted rational number is equal to the ratio of the product of the factorials of the primes in the first list to the product of the factorials of the primes in the second list.
Notes
- There may not be any primes that contained both in the first list and in the second list; however, a prime may appear as many times as one wishes in either list.
- The inputs can be assumed to each be (nonstrictly) between 1 and 65535; however, it cannot be assumed that the factorials of the numbers you will need to output will be in this range.
Example Input and Output
Here are examples of legal inputs and outputs.
input=>output
10,9 => [2,5],[3,3,3]
2,1 => [2],[]
3,1 => [3],[2]
1,5 => [2,3,2],[5] (elements of a list may be in any order)
3,2 => [3],[2,2]
6,1 => [3],[]
The inputs (2,2), (0,3), (3,0), (3,6) and (1,65536) are illegal inputs (i.e. your program doesn't need to behave in any particular way on them). Here are some examples of illegal outputs:
1,2 => [2],[2,2] (2 is in both returned lists)
5,2 => [5],[2,4] (4 is not prime)
2,1 => [2],[1] (1 is not prime either)
3,2 => [3],[2] (3!/2! = 3, not 3/2)
Scoring
This is code-golf, so the lowest score in bytes wins!
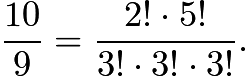
Does some sort of minimally reduced rational need to be given in the event there are multiple ways of expressing the answer? For example
10/9=[2*5]/[3*3]=[(2!/1!) * (5!/4!)] / [(3!/2!) * (3!/2!)]=[2! * 5! * 2! * 2!] / [3! * 3! * 1! * 4!]=(2! * 2! * 2! *5!) / (3! * 3! * 4!). – Digital Trauma – 2017-10-06T21:45:14.003@DigitalTrauma No; however, 4 is not prime, so the second one would not be valid. I believe (and can write up a proof in the question if you'd like) that any representation is unique. – Carl Schildkraut – 2017-10-06T22:02:51.263
Is it okay to take input as the fraction
10/9rather than a pair of numbers10and9? – Misha Lavrov – 2017-10-06T22:03:05.243@MishaLavrov Sure. I'll edit the question to reflect that. – Carl Schildkraut – 2017-10-06T22:03:22.007
@CarlSchildkraut Thanks - yes that helps - I thought I was missing something – Digital Trauma – 2017-10-06T22:04:46.590
Any reason there's a dot underneath the fraction bar in the image at the top? – Esolanging Fruit – 2017-10-10T01:39:59.157
@Challenger5 It's a period, part of the TeX from which I found the image on the Art of Problem Solving page that this problem is listed. – Carl Schildkraut – 2017-10-10T02:06:59.017