7
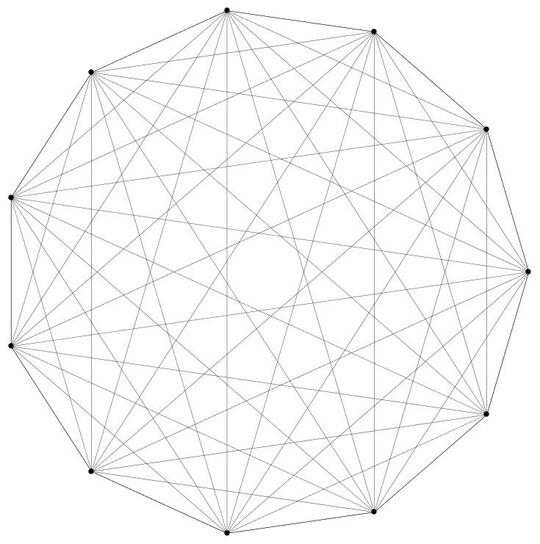
Let us consider a regular n-sided polygon where all of the sides are equal in length with n being a natural number larger than or equal to three. All of the vertices lie on the unit circle (circle of radius one centered at the origin) and one of the vertices is always at the coordinate (x,y)=(1,0). Now let's draw all possible diagonals (including the edges) which connect all n vertices to one another. Here is an example for n=11.
This results in n-choose-2 (which is just n(n-1)/2) lines (diagonals and edges) which in this case is 55. The total number of line intersections, counting the interior intersection points as well as the n vertices, will be denoted I and I=341 in this case.
The Goal
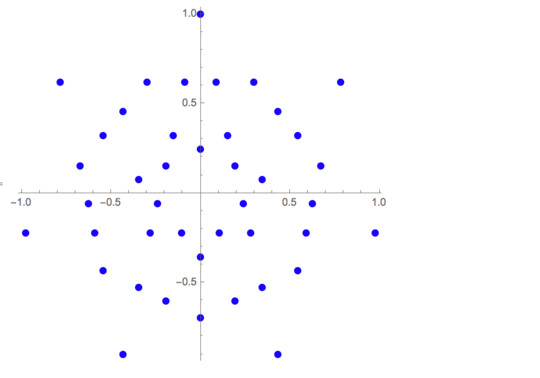
Your goal is to write a full program or a function which takes in an integer n larger than or equal to three and outputs a list of (x,y) coordinates of all of the intersections of all of the diagonals and edges, that are contained within the regular n-sided polygon with one of its vertices being at (1,0). This includes the n vertices themselves which lie on the unit circle. The length of this list must be I. There is an OEIS sequence for I, which is A007569 and here is a paper which talks about it.
Rules and Specifications
Each coordinate has to be an ordered 2-tuple, giving the (x,y) coordinates in the Cartesian system.
The list of coordinates can be in any order. It doesn't have to be sorted or in any particular order.
All of the coordinates provided must be accurate to at least six significant figures. I am not specifying a rounding method. You are free to choose any rounding method or to simply chop off a number. Also for n large enough, it will be the case that two distinct intersections (in exact arithmetic) will be equal to each other to six significant figures in both coordinates (in floating point arithmetic). In this case you are free to treat them as the "same" and remove the "duplicates" from your list. The length of your list will be less than I, but oh well!
The coordinates can be in decimal or scientific notation. For small enough n, decimal notation is fine and decimal notation will make it easier to check so it is preferred. But I am not mandating one over the other.
Outputting I, which should be the length of your coordinate list, is not a requirement for this task. You don't have to output it.
You can assume whatever input/output form that is appropriate for your language. You can also assume that the input will always be a positive integer greater than or equal to three. In case of any other input, your program is free to do whatever it wants. You can also assume that the input and output will always be in the numerical range of your language/environment. Trailing newlines are okay in the output.
Some Test Cases
I am showing more significant digits here than I need to. You are only required to show six. Remember, you don't have to print I.
n => 3
I => 3
(1.000000000,0)
(-0.5000000000,0.8660254038)
(-0.5000000000,-0.8660254038)
n => 4
I => 5
(1.000000000,0)
(0,1.000000000)
(-1.000000000,0)
(0,0)
(0,-1.000000000)
n => 5
I => 10
(1.000000000,0)
(0.3090169944,0.9510565163)
(-0.8090169944,0.5877852523)
(-0.1180339887,0.3632712640)
(0.3090169944,0.2245139883)
(-0.8090169944,-0.5877852523)
(0.3090169944,-0.2245139883)
(-0.1180339887,-0.3632712640)
(0.3090169944,-0.9510565163)
(-0.3819660113,0)
n => 6
I => 19
(1.000000000,0)
(0.5000000000,0.8660254038)
(-0.5000000000,0.8660254038)
(0,0.5773502692)
(0.2500000000,0.4330127019)
(0.5000000000,0.2886751346)
(-1.000000000,0)
(0,0)
(0.5000000000,0)
(-0.5000000000,0)
(-0.5000000000,-0.8660254038)
(0.5000000000,-0.2886751346)
(0.2500000000,-0.4330127019)
(0,-0.5773502692)
(0.5000000000,-0.8660254038)
(-0.5000000000,0.2886751346)
(-0.2500000000,0.4330127019)
(-0.2500000000,-0.4330127019)
(-0.5000000000,-0.2886751346)
n => 7
I => 42
(1.000000000,0)
(0.6234898019,0.7818314825)
(-0.2225209340,0.9749279122)
(0.1539892642,0.6746710485)
(0.3215520661,0.5410441731)
(0.4559270000,0.4338837391)
(0.6234898019,0.3002568637)
(-0.9009688679,0.4338837391)
(-0.05495813209,0.2407873094)
(0.3215520661,0.1548513136)
(0.6234898019,0.08593599577)
(-0.5244586698,0.3479477434)
(-0.2225209340,0.2790324255)
(0.1539892642,0.1930964297)
(-0.9009688679,-0.4338837391)
(0.1539892642,-0.1930964297)
(0.6234898019,-0.08593599577)
(-0.2225209340,-0.2790324255)
(0.3215520661,-0.1548513136)
(-0.5244586698,-0.3479477434)
(-0.05495813209,-0.2407873094)
(-0.2225209340,-0.9749279122)
(0.6234898019,-0.3002568637)
(0.4559270000,-0.4338837391)
(0.3215520661,-0.5410441731)
(0.1539892642,-0.6746710485)
(0.6234898019,-0.7818314825)
(-0.4314683302,0.5410441731)
(-0.2225209340,0.5887350528)
(-0.05495813209,0.6269801688)
(-0.2225209340,0.1071604339)
(0.07941680185,0.3479477434)
(-0.5990311321,-0.1930964297)
(-0.3568958679,0)
(0.2469796037,0)
(0.07941680185,-0.3479477434)
(-0.05495813209,-0.6269801688)
(-0.6920214716,0)
(-0.5990311321,0.1930964297)
(-0.2225209340,-0.1071604339)
(-0.2225209340,-0.5887350528)
(-0.4314683302,-0.5410441731)
I can provide more test cases but they will take up a lot of space and I am not sure how to provide them here. Let me know if you guys need more cases and what is the best way for me to provide them.
Scoring
This is code-golf. The answer with the smallest byte-count will win. In case of a tie, I will pick the answer that was posted earlier as the winner.
Please post your answer in the standard format with all compiler/interpreter options/flags.
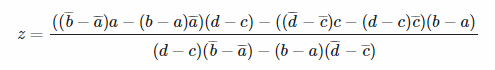
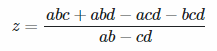
Are three-line intersections (such as the center of the hexagon) counted once or twice? – Luis Mendo – 2017-09-28T10:28:19.520
@LuisMendo No matter how many lines intersect at a point, the point is only counted once. – Fixed Point – 2017-09-28T15:46:03.933