Cyclotomic polynomial

Question

Background (skip to definitions)

Euler proved a beautiful theorem about the complex numbers: e^ix = cos(x) + i sin(x).

This makes de Moivre's theorem easy to prove:

(e^ix)ⁿ = e^i(nx)

(cos(x) + i sin(x))ⁿ = cos(nx) + i sin(nx)

We can plot complex numbers using the two-dimensional Euclidean plane, with the horizontal axis representing the real part and the vertical axis representing the imaginary part. This way, (3,4) would correspond to the complex number 3+4i.

If you are familiar with polar coordinates, (3,4) would be (5,arctan(4/3)) in polar coordinates. The first number, r, is the distance of the point from the origin; the second number, θ, is the angle measured from the positive x-axis to the point, counter-clockwise. As a result, 3 = r cosθ and 4 = r sinθ. Therefore, we can write 3+4i as r cosθ + r i sinθ = r(cosθ + i sinθ) = re^iθ.

Let us solve the complex equation zⁿ = 1, where n is a positive integer.

We let z = re^iθ. Then, zⁿ = rⁿe^inθ. The distance of zⁿ from the origin is rⁿ, and the angle is nθ. However, we know that the distance of 1 from the origin is 1, and the angle is 0. Therefore, rⁿ=1 and nθ=0. However, if you rotate by 2π more, you still end up at the same point, because 2π is just a full circle. Therefore, r=1 and nθ = 2kπ, giving us z=e^2ikπ/n.

We restate our discovery: the solutions to zⁿ=1 are z=e^2ikπ/n.

A polynomial can be expressed in terms of its roots. For example, the roots of x²-3x+2 are 1 and 2, so x²-3x+2 = (x-1)(x-2). Similarly, from our discovery above:

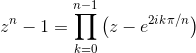
However, that product certainly contained roots of other n. For example, take n=8. The roots of z⁴=1 would also be included inside the roots of z⁸=1, since z⁴=1 implies z⁸ = (z⁴)² = 1² = 1. Take n=6 as an example. If z²=1, then we would also have z⁶=1. Likewise, if z³=1, then z⁶=1.

If we want to extract the roots unique to zⁿ=1, we would need k and n to share no common divisor except 1. Or else, if they share a common divisor d where d>1, then z would be the (k/d)-th root of z^n/d=1. Using the technique above to write the polynomial in terms of its roots, we obtain the polynomial:

Note that this polynomial is done by removing the roots of z^n/d=1 with d being a divisor of n. We claim that the polynomial above has integer coefficients. Consider the LCM of the polynomials in the form of z^n/d-1 where d>1 and d divides n. The roots of the LCM are exactly the roots we wish to remove. Since each component has integer coefficients, the LCM also has integer coefficients. Since the LCM divides zⁿ-1, the quotient must be a polynomial with integer coefficient, and the quotient is the polynomial above.

The roots of zⁿ=1 all have radius 1, so they form a circle. The polynomial represents the points of the circle unique to n, so in a sense the polynomials form a partition of the circle. Therefore, the polynomial above is the n-th cyclotomic polynomial. (cyclo- = circle; tom- = to cut)

Definition 1

The n-th cyclotomic polynomial, denoted , is the unique polynomial with integer coefficients that divide xⁿ-1 but not x^k-1 for k<n.

Definition 2

The cyclotomic polynomials are a set of polynomials, one for each positive integer, such that:

where k | n means k divides n.

Definition 3

The n-th cyclotomic polynomial is the polynomial xⁿ-1 divided by the LCM of the polynomials in the form x^k-1 where k divides n and k<n.

Examples

1. Φ₁(x) = x - 1
2. Φ₂(x) = x + 1
3. Φ₃(x) = x² + x + 1
4. Φ₃₀(x) = x⁸ + x⁷ - x⁵ - x⁴ - x³ + x + 1
5. Φ₁₀₅(x) = x⁴⁸ + x⁴⁷ + x⁴⁶ - x⁴³ - x⁴² - 2x⁴¹ - x⁴⁰ - x³⁹ + x³⁶ + x³⁵ + x³⁴ + x³³ + x³² + x³¹ - x²⁸ - x²⁶ - x²⁴ - x²² - x²⁰ + x¹⁷ + x¹⁶ + x¹⁵ + x¹⁴ + x¹³ + x¹² - x⁹ - x⁸ - 2x⁷ - x⁶ - x⁵ + x² + x + 1

Task

Given a positive integer n, return the n-th cyclotomic polynomial as defined above, in a reasonable format (i.e. e.g. list of coefficients is allowed).

Rules

You may return floating point/complex numbers as long as they round to the correct value.

Scoring

This is code-golf. Shortest answer in bytes wins.

References

• Wolfram MathWorld
• Wikipedia

Answer 1

Haskell, 120 bytes

import Data.Complex
p%a=zipWith(\x y->x-a*y)(p++[0])$0:p
f n=foldl(%)[1][cis(2*pi/fromInteger n)^^k|k<-[1..n],gcd n k<2]

Try it online!

Gives a list of complex floats that has entries like 1.0000000000000078 :+ 3.314015728506092e-14 due to float inacurracy. A direct method of multiplying out to recover the polynomial from its roots.

The fromInteger is a big concession to Haskell's type system. There's got to be a better way. Suggestions are welcome. Dealing with roots of unity symbolically might also work.

---

Haskell, 127 bytes

(h:t)%q|all(==0)t=[]|1>0=h:zipWith(\x y->x-h*y)t q%q
f n=foldl(%)(1:(0<$[2..n])++[-1])[tail$f k++[0,0..]|k<-[1..n-1],mod n k<1]

Try it online!

No imports.

Uses the formula

Computes Φ_n(x) by dividing the LHS by each of the other terms in the RHS.

The operator % does division on polynomials, relying on the remainder being zero. The divisor is assumed to be monic, and is given without the leading 1, and also with infinite trailing zeroes to avoid truncating when doing zipWith.

Answer 2

Mathematica, 43 41 bytes

Factor[x^#-1]/Times@@#0/@Most@Divisors@#&

Of course, we can always use the built-in, but if we don't, this divides xⁿ-1 by Φ_k(x) (computed recursively) for every proper divisor k of n.

We use Factor to get a polynomial at the end. I think the reason this works is that x^#-1 factors into all the cyclotomic polynomials of divisors of n, and then we divide out the ones we don't want.

-2 bytes thanks to Jenny_mathy, rewriting the Factor to only apply to the numerator.

Answer 3

MATL, 32 31 27 25 bytes

Z\"@:@/]XHxvHX~18L*Ze1$Yn

Output may be non-integer due to floating-point inaccuracies (which is allowed). The footer does rounding for clarity.

Try it online!

Answer 4

Haskell, 250 236 233 218 216 bytes

This is a verbose version, (@xnor can do it in almost half the score) but it is guaranteed to work for any n as long as you have enough memory, but it does not use a builtin for generating the n-th cyclotomic polynomial. The input is an arbitrary size integer and the output is a polynomial type with (exact) rational coefficients.

The rough idea here is calculatin the polynomials recursively. For n=1 or n prime it is trivial. For all other numbers this approach basically uses the formula from definition 2

solved for . Thanks @H.PWiz for quite a bunch of bytes!

import Math.Polynomial
import Data.Ratio
import NumberTheory
p=powPoly x
q=poly LE
c n|n<2=q[-1,1%1]|isPrime n=sumPolys$p<$>[0..n-1]|1>0=fst$quotRemPoly(addPoly(p n)$q[-1])$foldl1 multPoly[c d|d<-[1..n-1],n`mod`d<1]

For n=105 this yields following polynomial (I tidied up all the %1 denominators):

[1,1,1,0,0,-1,-1,-2,-1,-1,0,0,1,1,1,1,1,1,0,0,-1,0,-1,0,-1,0,-1,0,-1,0,0,1,1,1,1,1,1,0,0,-1,-1,-2,-1,-1,0,0,1,1,1]

The polynomial for n=15015 can be found here (the largest coefficient is 23).

Try it online!

Answer 5

Jelly, 23 bytes

R÷
ÆḌÇ€FQœ-@Ç×ı2×ØPÆeÆṛ

Try it online!

Outputs as a list of coefficients.

Has floating point AND complex inaccuracies. Footer does rounding to make output prettier.

Answer 6

J, 36 bytes

1+//.@(*/)/@(,.~-)_1^2*%*i.#~1=i.+.]

Try it online!

Uses the formula

There are some floating-point inaccuracies, but it is allowed.

Answer 7

Mathematica, 81 bytes

Round@CoefficientList[Times@@(x-E^(2Pi*I#/k)&/@Select[Range[k=#],#~GCD~k<2&]),x]&

Answer 8

R, 176 171 139 112 bytes

function(n){for(r in exp(2i*pi*(x=1:n)[(g=function(x,y)ifelse(o<-x%%y,g(y,o),y))(x,n)<2]/n))T=c(0,T)-r*c(T,0)
T}

Try it online!

Massively simpler version; uses a for loop rather than a Reduce.

Answer 9

Pari/GP, 8 bytes

A built-in.

polcyclo

Try it online!

---

Pari/GP, 39 bytes, without built-in

f(n)=p=x^n-1;fordiv(n,d,d<n&&p/=f(d));p

Using the formula:

\$ \Phi_n(x)=\dfrac{x^{n}-1}{\prod\limits_{\stackrel{d|n}{{}_{d<n}}}\Phi_{d}(x)} \$.

Try it online!

Answer 10

CJam (52 51 bytes)

{M{:K,:!W+K,0-{K\%!},{j($,\:Q,-[{(\1$Qf*.-}*;]}/}j}

Online demo. This is an anonymous block (function) which takes an integer on the stack and leaves a big-endian array of coefficients on the stack.

Dissection

{                    e# Define a block
  M{                 e#   Memoised recursion with no base cases.
    :K,:!W+          e#     Store argument in K and build (x^K - 1)
    K,0-{K\%!},      e#     Find proper divisors of K
    {                e#     Foreach proper divisor D...
      j              e#       Recursive call to get Dth cyclotomic poly
      ($,\:Q,-       e#       The cleverest bit. We know that it is monic, and the
                     e#       poly division is simpler without that leading 1, so
                     e#       pop it off and use it for a stack-based lookup in
                     e#       calculating the number of terms in the quotient.
                     e#       Ungolfed this was (;:Q1$,\,-
                     e#       Store the headless divisor in Q.
      [              e#       Gather terms into an array...
        {            e#         Repeat the calculated number of times...
          (\         e#           Pop leading term, which goes into the quotient.
          1$Qf*.-    e#           Multiply Q by that term and subtract from tail.
        }*;          e#         Discard the array of Q,( zeroes. 
      ]
    }/
  }j
}

Answer 11

JavaScript(ES6), 337 333 284 ... 252 250 245 242 bytes

(v,z=[e=[1,u=0]],g=(x,y)=>y?g(y,x%y):x,h=Math,m=(l,x,p=h.cos(l),q=h.sin(l),i=0)=>x.map(()=>[(i&&(n=x[i-1])[0])-(w=x[i])[0]*p+w[1]*q,(i++&&n[1])-w[1]*p-w[0]*q]))=>{for(;++u<v;z=g(v,u)-1?z:[...m(h.PI*2*u/v,z),e]);return z.map(r=>h.round(r[0]))}

Explanation (Selected):

z=[e=[1,u=0]]

Initialize z=(1+0i) * x^0

g=(x,y)=>y?g(y,x%y):x

GCD calculation.

h=Math

Since I need to use Math functions quite a lot, I used another variable here.

m=(l,x,p=h.cos(l),q=h.sin(l),i=-1)=>blah blah blah

Polynomial multiplication.

for(;++u<v;z=g(v,u)-1?z:[...m(h.PI*2*u/v,z),e]);

The formula used is

return z.map(r=>h.round(r[0]))

Compress the output back to an integer array.

Outputs:

An array of integers, with the element at position i representing the coefficient of x^i.

One of the problem JS have is that since JS does not provide native library for calculations on polynomials and complex numbers, they needed to be implemented in an array-like way.

console.log(phi(105)) gives

Array(49)
 0:  1    1:  1    2:  1    3: -0    4: -0    5: -1    6: -1 
 7: -2    8: -1    9: -1   10:  0   11: -0   12:  1   13:  1 
14:  1   15:  1   16:  1   17:  1   18:  0   19: -0   20: -1 
21:  0   22: -1   23: -0   24: -1   25:  0   26: -1   27: -0 
28: -1   29:  0   30:  0   31:  1   32:  1   33:  1   34:  1 
35:  1   36:  1   37: -0   38: -0   39: -1   40: -1   41: -2 
42: -1   43: -1   44: -0   45: -0   46:  1   47:  1   48:  1 
length: 49
__proto__: Array(0)

337>333(-4): Changed the code for checking undefined value

333>284(-49): Changed the polynomial multiplication function because it can be simplified

284>277(-7): Deleted some redundant code

277>265(-12): Use 2 variables instead of a 2-element array to drop some bytes in array usage

265>264(-1): Use Array.push() instead of Array.concat() to reduce 4 bytes, but added 3 for the for-loop braces and the z variable

264>263(-1): Further golfed on the last amendment

263>262(-1): Golfed on the for loop

262>260(-2): Golfed out the if clause

260>258(-2): Further combined the declarations

258>252(-6): Golfed on reuse of array references

252>250(-2): Replace some unary operators as binary operators

250>245(-5): Move the increment in Array.map() to the last reference of counter to remove bytes

245>242(-3): Use spread syntax instead of Array.push()