Which tetromino is this?

Question

Given an unsigned 16-bit integer N, your task is to determine whether its binary representation mapped inside a 4x4 matrix is matching a tetromino shape, and if so, which shape it is.

Matrix

Each bit of N is mapped inside a 4x4 matrix, from left to right and from top to bottom, starting with the most significant one.

Example:

N = 17600
binary representation: 0100010011000000
matrix: [ [ 0, 1, 0, 0 ],
          [ 0, 1, 0, 0 ],
          [ 1, 1, 0, 0 ],
          [ 0, 0, 0, 0 ] ]

Tetromino shapes

Base shapes

There are 7 tetromino shapes, identified by the letters O, I, S, Z, L, J and T:

Rotations and translations

If a shape is translated and/or rotated within the 4x4 matrix, it is still considered a valid variation of the same tetromino. For instance, 17600, 1136, 2272 and 1604 should all be identified as J tetrominoes:

Don't wrap!

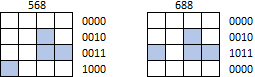
However, the shapes can't wrap around or be shifted beyond any boundary of the matrix. For instance, neither 568 nor 688 should be identified as J tetrominoes (let alone any other shape):

Clarifications and rules

• You may take input as an integer, or directly as 16 binary digits in any reasonable format, such as a 2D array, a flat array or a delimited string.
• The input is guaranteed to be an unsigned 16-bit integer (or its equivalent representation as an array or a string).
• When a valid shape is identified, you must print or return the letter identifying the shape, in either lower or upper case.
• If no shape is identified, you must print or return a value that doesn't match any tetromino letter. You may also choose to return nothing at all.
• To be considered valid, the matrix must contain the exact tetromino shape without any additional cells (see 1911 and 34953 in the test cases).
• This is code-golf, so the shortest answer in bytes wins!

Test cases

You can follow this link to get the test cases as 2D arrays.

0      -> false
50     -> false
51     -> 'O'
1911   -> false
15     -> 'I'
34952  -> 'I'
34953  -> false
1122   -> 'S'
3168   -> 'Z'
785    -> 'L'
1136   -> 'J'
568    -> false
688    -> false
35968  -> 'T'
19520  -> 'T'

Answer 1

Jelly,  54 43 42  41 bytes

-1 byte thanks to Erik the Outgolfer (move transpose inside repeated chain)

T€FṀ⁸ṙ€Zµ⁺F
ZU$3СǀḄṂ“çc3Ð6'G‘i’ị“¥Çıƭ⁵»

A monadic link taking a 2D array of integers (1s and 0s) and returning a lowercase letter oiszljt for the respective tetromino orw if invalid.

Try it Online! or see the test suite.

Also see this program which lists all 1820 possible 2D binary arrays with exactly four bits set along with their outputs, sorted by those outputs.

How?

This first takes all four rotations of the input. Then it shifts the set bits of each as far to the right and then as far to the bottom as possible and converts the results to binary numbers. It then looks up the minimum result in a list of the minimal such representations of each valid tetromino and uses the decremented result to index into the two concatenated dictionary words zoist+jowl, yielding w when no match was found.

T€FṀ⁸ṙ€Zµ⁺F - Link 1, shift set bits right & then down : list of lists of bits          
        µ⁺  - perform the following twice, 1st with x=input, then with x=result of that):
T€          -   truthy indexes of €ach
  F         -   flatten into a single list
   Ṁ        -   maximum (the index of the right-most bit)
    ⁸       -   chain's left argument, x
     ṙ€     -   rotate €ach left by that amount
       Z    -   transpose the result
          F - flatten (avoids an € in the main link moving this into here)

ZU$3СǀḄṂ“çc3Ð6'G‘i’ị“¥Çıƭ⁵» - Main link: list of lists of bits (the integers 0 or 1)
   3С                        - repeat this 3 times collecting the 4 results:
  $                           -   last two links as a monad:
Z                             -     transpose
 U                            -     upend (reverse each) -- net effect rotate 90° CW
      Ç€                      - call the last link as a monad for €ach
        Ḅ                     - convert from binary (vectorises)
         Ṃ                    - minimum (of the four results)
          “çc3Ð6'G‘           - code-page indexes = [23,99,51,15,54,39,71]
                              -   ...the minimal such results for l,z,o,i,s,t,j shapes
                   i          - 1-based index of minimum in there or 0 if not found
                    ’         - decrement
                      “¥Çıƭ⁵» - compressed words: "zoist"+"jowl" = "zoistjowl"
                     ị        - index into (1 indexed & modular, so -1 yields 'w',
                              -             0 yields 'l', 1 yields 'z', ...)

---

Previous method (54 bytes)

Fœr0Ḅ“çc3Ðñ'G‘i
;Z$Ḅ©f“¦µ½¿Æ‘ȯ®¬S>2ȧZU$3СǀṀ’ị“¥Çıƭ⁵»

A monadic link taking a 2D array of integers (1s and 0s) and returning a lowercase letter oiszljt for the respective tetromino or w if invalid.

Try it online!

This checks there are at least three empty lines (rows+columns) and that certain patterns of bits are not present in any line (specifically the numbers 5,9,10,11, and 13), these together assure the next step wont yield false-positives. It then flattens and then floor-shifts the binary number (by striping trailing zeros before conversion) of each of the four rotations, and looks up the minimal result in a list of numbers, using the decremented result to index into the two concatenated dictionary words zoist+jowl, yielding w when no match was found.

Answer 2

Python 3, 124 bytes

def f(n):
 while n&4369<n/n:n>>=1
 while n&15<1:n>>=4
 return'TJLZSIO'["rēȣc63ıGtIJȱᄑ@'̢̑@@@@Ȳq".index(chr(n))%7]

Try it online!

Expects an integer n representing a 4 × 4 binary matrix. Throws if no tetromino is found.

Line 2 slides the shape to the right until a 1 is in the rightmost column. (4369 is 0001 0001 0001 0001 in binary.) Line 3 lowers the shape until a 1 is in the bottom row. Together this turns e.g.:

    0 1 0 0        0 0 0 0
    1 1 1 0  into  0 0 0 0
    0 0 0 0        0 0 1 0
    0 0 0 0        0 1 1 1

Then we look for the index of n in this list:

 [114  275  547   99   54   15   51
  305   71  116  306  561 4369   64
   39  802  785   64   64   64   64
  562  113   23]
#   T    J    L    Z    S    I    O

Each column of indices equivalent modulo 7 corresponds to a tetromino shape. 64 (@) is used as a padding value as n cannot be 64 at this point in the code.

NB. An exception is thrown for input 0 by computing n/n instead of 1.

Answer 3

APL (Dyalog), 95 94 93 89 87 bytes

-2 thanks to Zacharý

Requires ⎕IO←0 which is default on many systems. Takes Boolean matrix (of any shape!) as argument. Returns nothing if the given number of bits is not four, and a blank line if the four given bits do not form a tetromino.

{4=+/,⍵:'OIZSJLT'/⍨∨/1∊¨(((2 2)4⍴¨1),(0 1⌽¨⊂K⌽2⊖J),(⍳3)⊖¨⊂J←1,⍪K←3↑1)∘.⍷⍵∘{⌽∘⍉⍣⍵⊢⍺}¨⍳4}

Try it online!

Works by creating all four rotations of the input, then looking for each tetromino in each rotation.

{…} anonymous function where the argument is represented by ⍵:

 ,⍵ ravel (flatten) the argument

 +/ sum it

 4= is four equal to that?

 : if so, then (else return nothing):

  ⍳4 first four ɩndices; [0,1,2,3]

  ⍵∘{…}¨ apply the following function on each, using the input as fixed left argument

   ⍺ the left argument i.e. the input

   ⊢⍺ yield that (separates ⍵ from ⍺)

   ⌽∘⍉⍣⍵ mirror and transpose (i.e. rotate 90°) ⍵ times

  (…)∘.⍷ outer "product", but using Find*, of the following list and the rotations:

   3↑1 take three elements from one, padding with zeros; [1,0,0]

   K← store that as K

   ⍪ table (make into column vector); [[1],[0],[0]]

   1, prepend a one; [[1,1],[1,0],[1,0]] ("J")

   J← store as J

   (…)⊖¨⊂ rotate the entire J vertically, each of the following number of steps:

    ⍳3 first three ɩntegers; [0,1,2]

   we have [[[1,1],[1,0],[1,0]],[[1,0],[1,0],[1,1]],[[1,0],[1,1],[1,0]]] ("J", "L, "T")

   (…), prepend the following list:

    2⊖J rotate J two steps vertically; [[1,0],[1,1],[1,0]] ("T")

    K⌽ rotate the rows of that by 1, 0, and 0 steps respectively; [[0,1],[1,1],[1,0]] ("Z")

    0 1⌽¨⊂ rotate the entire array vertically, no times and once; [[[0,1],[1,1],[1,0]],[[1,0],[1,1],[0,1]]] ("Z", "S")

    (…), prepend the following list:

     (2 2)4⍴¨1 reshape a one into each of a 2×2 matrix and a 4-element list; [[[1,1],[1,1]],[1,1,1,1]] ("O", "I")

  1∊¨ for each, is one a member?

  ∨/ horizontal OR reduction (i.e. across rotations; one Boolean for each shape)

  'OIZSLJT'/⍨ use that to filter the string

* Find returns a Boolean array of same shape as its right argument, with ones indicating the top left corner of all subarrays identical to the left argument.

Answer 4

JavaScript (ES6), 242 212 172 164 bytes

x=>[...'OISZLJT'].filter((z,y)=>x.match(`^0*(${'99,33825|15,51|2145,195|561,2115|57,1059|135,71|1073'.split`,`[y].replace(/\d+/g,C=x=>x?x%2+C(x>>1)+x%2:'|')})0*$`))

Was supposed to be just to get the ball rolling, but I'm a little late for that ¯\_(ツ)_/¯

Takes a string of bits, with rows separated by 0s ('0001000110001000000' representing 0001 0011 0010 0000) and returns an array containing the character representing the tetromino, or an array containing nothing.

This works by checking each rotation of tetromino to see if the input at any point contains the tetromino, surrounded entirely by zeroes on either side. Each tetromino is represented by one or more binary numbers:

0 0 0 0   -> 0000 0110 1100 0000
0 1 1 0   -> 0000001100110000000
1 1 0 0   -> 110011
0 0 0 0   -> 51

0 1 0 0   -> 0100 0110 0010 0000
0 1 1 0   -> 0100001100001000000
0 0 1 0   -> 100001100001
0 0 0 0   -> 2145

So to check if the input contains an S tetromino, we simply check whether it contains the binary representation of either 51 or 2145, with only 0s on either side.

A few of the tetrominoes have 4 orientations. If you look at the binary representations of these, each has 2 representations which are simply the mirror of the other two. To save space, the binary representation is built up forward and backward simultaneously with the recursive C function, allowing us to only put two of the orientations in and have the other two implied.

---

Alternate approach with charcodes:

x=>[...'OISZLJT'].filter((z,y)=>x.match(`^0*(${[...'÷,êÿ,óî,ûÝ,ëúüÏ,çöïþ,ßýíÞ'.split`,`[y]].map(c=>(C=n=>n?'1e'+(n%4+2)%5-0+C(n>>2):'')(c.charCodeAt())).join`|`})0*$`))

Answer 5

Jelly, 53 bytes

ZL0ẋW⁸tZµ⁺ZU$3С“©©“œ“Ç¿“¦©¦“ƽ‘;Uḃ2$’¤iЀṀị“÷¶Ė¡µỵỤ»

Try it online!

Full program. Takes a 4x4. Prints m if not a tetromino, otherwise prints lowercase.

Answer 6

MATL, 60 bytes

Itt6tIl7tl7H15vHe"4:"G@X!HYa]4$v@BIthYaEqY+4=aa]v'OSZLJTI'w)

Input is a binary 4×4 array (matrix), using ; as row separator. Ouput is a letter or empty for no tetromino.

Try it online! Or verify all test cases (output has a dot appended to allow identifying an empty result).

Explanation

The code builds 4 rotations of the input 4×4 array in steps of 90 degrees. Each rotated array is padded with 2 zeros up and down, which transforms it into a 8×4 array. The 4 arrays are vertically concatenated into a 32×4 array. The four rotated arrays within this concatenated array are "isolated" thanks to the zero-padding.

Each of the 7 possible patterns is tested to see if it is present in the 32×4 array. A loop is used for this. Each pattern is defined by two numbers, which expressed in binary give the appropriate 0/1 mask. For example, numbers 3, 6 define the "S" shape.

The 7 sets of 2 numbers are arranged into a 2×7 matrix, from which the loop will pick each column sequentially. The matrix is defined by pushing all numbers to the stack, contatenating them into a vector, and reshaping into a 2-row matrix. Since the "I" shape is defined by number 15 followed by 0, putting it at the end allows the 0 to be implicitly filled by the reshaping function.

The mask is then padded with 3 zeros in the four directions. This is necessary so as to detect unwanted values in the input.

To see if the mask is present in the 32×4 array, the latter is transformed to bipolar form (i.e. −1/1 instead of 0/1) and convolved with the mask. Since the mask has 4 ones, matching occurs if some entry in the convolution result equals 4.

At the end of the loop, 7 false/true results have been obtained, at most one of which is true. This is used to index into a string containing the possible output letters.

Answer 7

Retina, 125 bytes

s`(.*1){5}.*

{s`.*1111.*
I
s`.*111(.{2,4})1.*
$.1
T`234`\LTJ
s`.*11(.{2,4})11.*
$.1
T`2-90`S\OZ4-9
s`.*4.*

O#$`.
$.%`
O#$^`

Try it online! Link includes test cases plus a header to convert from integers to a 4×4 matrix. Explanation:

s`(.*1){5}.*

Delete the input if it contains 5 1s.

{s`.*1111.*
I

Check all rotations of the input (see below). If the input contains four consecutive 1s, it's an I.

s`.*111(.{2,4})1.*
$.1
T`234`\LTJ

If it contains three consecutive 1s plus a 1 on the next line underneath one of the three, then map the number of intermediate characters to the appropriate result letter.

s`.*11(.{2,4})11.*
$.1

Similarly for two adjacent 1s adjacent to two adjacent 1s on the next line.

T`2-90`S\OZ4-9

But also keep count of the number of rotations using the otherwise unused 0s.

s`.*4.*

And give up if too many rotations have been performed.

O#$`.
$.%`
O#$^`

Transpose and reverse the array, thus rotating it.

Answer 8

Perl 5, 197 + 1 (-p) = 198 bytes

s/(0000)*$//;1while s/(...)0(...)0(...)0(...)0/0${1}0${2}0${3}0${4}/;$_={51,O,15,I,4369,I,54,S,561,S,99,Z,306,Z,547,L,23,L,785,L,116,L,275,J,113,J,802,J,71,J,114,T,562,T,39,T,609,T}->{oct("0b".$_)}

Try it online!

Takes a 16 bit string as input. Outputs nothing if input is not a single tetromino.

How?

The two substitutions "move" the input shape to the bottom right corner. The resulting bit string is converted to an integer, then checked for in a hash of valid integers.

Answer 9

APL (Dyalog), 66 bytes

{'TIOJSLZ-'[(¯51 144 64,,∘+⍨12J96 ¯48J64)⍳×/(+/-4×⊢)⍵/,0j1⊥¨⍳4 4]}

Try it online!

The arg is a boolean vector.

Computes signed distances of the dots to their centre of gravity as complex numbers (real and imaginary part are ∆x,∆y) and multiplies the complex numbers together. This turns out to be a good enough invariant to distinguish among the tetrominoes.