How does the square end?

Question

In Base-10, all perfect squares end in 0, 1, 4, 5, 6, or 9.

In Base-16, all perfect squares end in 0, 1, 4, or 9.

Nilknarf describes why this is and how to work this out very well in this answer, but I'll also give a brief description here:

When squaring a Base-10 number, N, the "ones" digit is not affected by what's in the "tens" digit, or the "hundreds" digit, and so on. Only the "ones" digit in N affects the "ones" digit in N², so an easy (but maybe not golfiest) way to find all possible last digits for N² is to find n² mod 10 for all 0 <= n < 10. Each result is a possible last digit. For Base-m, you could find n² mod m for all 0 <= n < m.

Write a program which, when given the input N, outputs all possible last digits for a perfect square in Base-N (without duplicates). You may assume N is greater than 0, and that N is small enough that N² won't overflow (If you can test all the way up to N², I'll give you a finite amount of brownie points, but know that the exchange rate of brownie points to real points is infinity to one).

Tests:

 Input -> Output
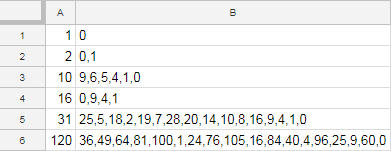
 1     -> 0
 2     -> 0,1
 10    -> 0,1,5,6,4,9
 16    -> 0,1,4,9
 31    -> 0,1,2,4,5,7,8,9,10,14,16,18,19,20,25,28
 120   -> 0,1,4,9,16,24,25,36,40,49,60,64,76,81,84,96,100,105

this is code-golf, so standard rules apply!

(If you find this too easy, or you want a more in-depth question on the topic, consider this question: Minimal cover of bases for quadratic residue testing of squareness).

Answer 1

Jelly, 5 bytes

R²%³Q

Try it online!

Explanation

R²%³Q   Main link, argument: n

R       Range from 1 to n
 ²      Square each
  %³    Mod each by n
    Q   Deduplicate

Answer 2

Google Sheets, 52 51 47 bytes

=ArrayFormula(Join(",",Unique(Mod(Row(A:A)^2,A1

_{^{Saved 4 bytes thanks to Taylor Scott}}

Sheets will automatically add 4 closing parentheses to the end of the formula.

It doesn't return the results in ascending order but it does return the correct results.

Answer 3

05AB1E, 5 bytes

Lns%ê

Try it online! or as a Test Suite

L     # Range 1 .. input
 n    # Square each
  s%  # Mod by input
    ê # Uniquify (also sorts as a bonus)

Answer 4

Swift, 47 35 32* bytes

* -3 thanks to @Alexander.

Possibly the first time in history Swift ties beats Python?

{m in Set((0..<m).map{$0*$0%m})}

Try it online!

---

Explanation

• (0..<m).map{} - Iterates through the range [0...m) and map the following results:

• $0*$0%m - The square of each integer modulo the base m.

• Set(...) - Removes the duplicates.

• m in - Assigns the base to a variable m

Answer 5

Japt, 7 6 bytes

Dz%UÃâ

Test it

1 byte saved thanks to Oliver

---

Explanation

Implicit input of integer U.

Ç   Ã

Create an array of integers from 0 to U-1, inclusive and pass each though a function.

²

Square.

%U

Modulo U.

â

Get all unique elements in the array and implicitly output the result.

Answer 6

Brachylog, 10 9 bytes

>ℕ^₂;?%≜ᶠ

Try it online!

Explanation

       ≜ᶠ       Find all numbers satisfying those constraints:
    ;?%           It must be the result of X mod Input where X…
  ^₂              …is a square…
>ℕ                …of an integer in [0, …, Input - 1]

Answer 7

C#, 63 bytes

using System.Linq;m=>new int[m].Select((_,n)=>n*n%m).Distinct()

Try it online!

Answer 8

JavaScript (ES6), 52 bytes

f=(m,k=m,x={})=>k?f(x[k*k%m]=m,k-1,x):Object.keys(x)

Test cases

f=(m,k=m,x={})=>k?f(x[k*k%m]=m,k-1,x):Object.keys(x)

;[1, 2, 10, 16, 31, 120]
.map(m => console.log(m + ' -> ' + f(m)))

---

Non-recursive version, 60 58 bytes

Saved 2 bytes thanks to @ThePirateBay

m=>(a=[...Array(m).keys()]).filter(v=>a.some(n=>n*n%m==v))

Test cases

let f =

m=>(a=[...Array(m).keys()]).filter(v=>a.some(n=>n*n%m==v))

;[1, 2, 10, 16, 31, 120]
.map(m => console.log(m + ' -> ' + f(m)))

Answer 9

Pyth, 6 bytes

{%RQ*R

Try it online

How it works

{%RQ*RdQ    implicit variables
       Q    autoinitialized to eval(input())
    *R      over [0, …, Q-1], map d ↦ d times
      d         d
 %R         map d ↦ d modulo
   Q            Q
{           deduplicate

Answer 10

Python 3, 40 39 37 bytes

-1 byte thanks to Mr. Xcoder. -2 bytes thanks to Business Cat.

lambda m:[*{n*n%m for n in range(m)}]

Try it online!

Answer 11

Actually, 11 bytes

;╗r⌠²╜@%⌡M╔

Try it online!

Explanation:

;╗r⌠²╜@%⌡M╔
;╗           store a copy of m in register 0
  r          range(m)
   ⌠²╜@%⌡M   for n in range:
    ²          n**2
     ╜@%       mod m
          ╔  remove duplicates

Answer 12

Haskell, 45 bytes

import Data.List
f m=nub[n^2`mod`m|n<-[0..m]]

-4 bytes from Anders Kaseorg

Try it online!

Answer 13

CJam, 12 bytes

{_,_.*\f%_&}

Anonymous block accepting a number and returning a list.

Try it online!

Explanation

_,          Copy n and get the range [0 .. n-1]
  _.*       Multiply each element by itself (square each)
     \f%    Mod each by n
        _&  Deduplicate

Answer 14

MATL, 6 5 bytes

-1 byte thanks to @LuisMendo

:UG\u

Try it online!

Answer 15

Scala, 32 30 bytes

Simple use of the easy tip from OP.

(0 to n-1).map(x=>x*x%n).toSet

Try it online!

-2 bytes thanks to @MrXcoder, with priorities (no need for () around * operation)

Wondering: is this possible to implicitly tell the compiler to understand things like (0 to n-1)map(x=>x*x%n)toSet (without having to import scala.language.postfixOps)?

Answer 16

Octave, 27 bytes

@(n)unique(mod((1:n).^2,n))

Try it online!

Answer 17

Mathematica, 30 bytes

Union@Table[Mod[i^2,#],{i,#}]&

Try it online!

Answer 18

JavaScript (ES6), 48 bytes

f=
n=>[...new Set([...Array(n)].map((_,i)=>i*i%n))]

<input type=number min=0 oninput=o.textContent=f(+this.value)><pre id=o>

43 bytes if returning a Set instead of an array is acceptable.

Answer 19

Haskell, 44 bytes

f m=[k|k<-[0..m],or[mod(n^2)m==k|n<-[0..m]]]

Try it online!

Answer 20

Retina, 70 bytes

.+
$*

;$`¶$`
1(?=.*;(.*))|;1*
$1
(1+)(?=((.*¶)+\1)?$)

D`1*¶
^|1+
$.&

Try it online! Warning: Slow for large inputs. Slightly faster 72-byte version:

.+
$*

$'¶$';
1(?=.*;(.*))|;1*
$1
+s`^((1+)¶.*)\2
$1
^1+

D`1*¶
^|1+
$.&

Try it online!

Answer 21

Clojure, 40 bytes

#(set(map(fn[x](mod(* x x)%))(range %)))

Answer 22

Ruby, 31 30 bytes

->m{(0..m).map{|n|n*n%m}.uniq}

Try it online!

Answer 23

Perl 6, 19 bytes

{set (^$_)»²X%$_}

Test it

Expanded:

{ # bare block lambda with implicit param ｢$_｣

  set        # turn the following into a Set (shorter than ｢unique｣)

      (
        ^$_  # a Range upto (and excluding) ｢$_｣
      )»²    # square each of them (possibly in parallel)

    X%       # cross modulus the squared values by

      $_     # the input
}

Answer 24

Pyth, 13 bytes

VQ aY.^N2Q){Y

Try online.

Lame attempt at explaining:

VQ               for N in [0 .. input-1]
                   blank space to supress implicit print inside the loop
     .^N2Q         N ^ 2 % input
   aY              append that to Y, which is initially an empty list
          )      end for
           {Y    deduplicate and implicit print

To sort the output, insert an S on any side of the {

I think there should be a shorter way...

Answer 25

Python 2, 59 bytes

t=int(input())
print list(set([(i*i)%t for i in range(t)]))

Try it online!

Answer 26

PowerShell, 35 bytes

0..($n="$args")|%{$_*$_%$n}|sort -u

Try it online!

Answer 27

R, 28 bytes

unique((1:(n<-scan()))^2%%n)

Try it online!

Answer 28

8th, 138 131 bytes

Code

[] swap dup >r ( 2 ^ r@ n:mod a:push ) 1 rot loop rdrop ' n:cmp a:sort ' n:cmp >r -1 a:@ swap ( tuck r@ w:exec ) a:filter rdrop nip

Explanation

[] - Create output array

swap dup >r - Save input for later use

( 2 ^ r@ n:mod a:push ) 1 rot loop - Compute square end

rdrop - Clean r-stack

' n:cmp a:sort - Sort output array

' n:cmp >r -1 a:@ swap ( tuck r@ w:exec ) a:filter rdrop nip - Get rid of consecutive duplicates from array

SED (Stack Effect Diagram) is: a -- a

Usage and example

: f [] swap dup >r ( 2 n:^ r@ n:mod a:push ) 1 rot loop rdrop ' n:cmp a:sort ' n:cmp >r -1 a:@ swap ( tuck r@ w:exec ) a:filter rdrop nip ;

ok> 120 f .
[0,1,4,9,16,24,25,36,40,49,60,64,76,81,84,96,100,105]

Answer 29

Java (OpenJDK 8), 86 77 bytes

n->java.util.stream.IntStream.range(1,n+1).map(a->a*a%n).distinct().toArray()

Try it online!

Answer 30

PHP, 53 bytes

for(;$i<$t=$argv[1];)$a[$z=$i++**2%$t]++?:print"$z
";

Loop from 0 to the input number, using the n^2 mod base formula to mark numbers that have been used. It goes to that position in an array, checking if it's been incremented and outputting it if it hasn't. It then increments it afterwards so duplicate values don't get printed.

Try it online!

Answer 31

Perl 5, 41 + 1 (-n) = 42 bytes

$k{$n++**2%$_}++while$n<$_;say for keys%k

Try it online!

Answer 32

Pari/GP, 25 bytes

n->Set([x^2%n|x<-[1..n]])

Try it online!