Build the blancmange function

Question

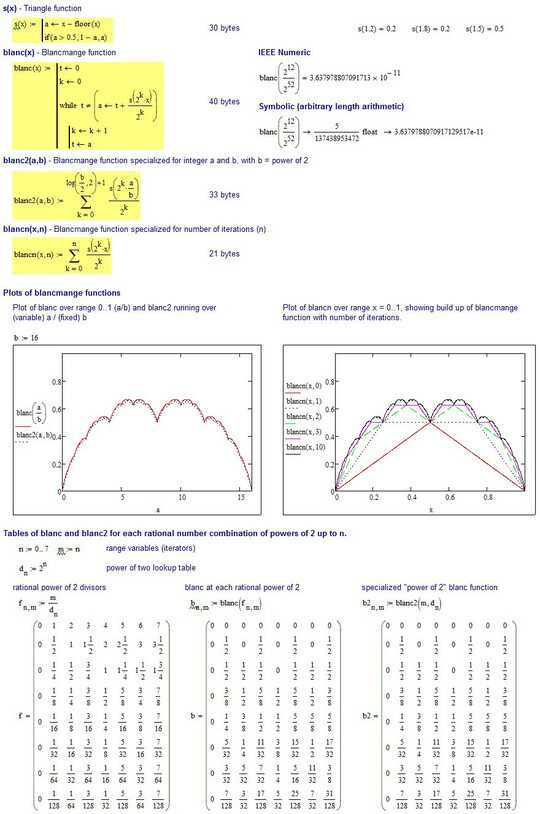
The blancmange function is used as an example in basic calculus of a function that is continuous everywhere, but differentiable nowhere. It achieves this effect by using the sums of ever-diminishing triangle-wave functions.

Your task is to build a program that takes a binary fractional number in the interval [0, 1] and returns the exact height of the blancmange curve at that position. Both fractions can be represented using the notation of your choice, but if you are using a nonstandard one (e.g. not IEEE floating-point or an integer with a fixed radix point), you must explain it in your solution, and your notation must support an accuracy of at least 2^-52.

Answer 1

Ruby, 53 characters

f=->x{x>0?f[2*x=x<0.5?x:1-x]/2+x: 0}
$><<f[gets.to_f]

expanded:

f = lambda do |x|
  if i>0
    x = 1 - x unless x < 0.5
    return x + f[2*x] / 2
  else
    return 0
  end
end  

print f[gets.to_f]

The input is a decimal value, assumed to be in the range 0..1 . The output is a decimal value. The platform native double precision numeric type is used, and is assumed to be at least 53 bits of mantissa. Since every floating point value in a binary fraction, this algorithm will always terminate after at most 53 (with the default precision) steps.

Answer 2

Mathematica 92 chars

This uses exact arithmetic (fractions).

b@n_:=FoldList[#+{1,#2}/2^n&,{0,0},
Total/@ (2 Reverse[IntegerDigits[#,2,n]&/@Range[0,2^n-1]]-1)]

{{{0, 0}, {1/2, 1/2}, {1, 0}}, {{0, 0}, {1/4, 1/2}, {1/2, 1/2}, {3/4, 1/2}, {1, 0}}, {{0, 0}, {1/8, 3/8}, {1/4, 1/2}, {3/8, 5/8}, {1/2, 1/2}, {5/8, 5/8}, {3/4, 1/2}, {7/8, 3/8}, {1, 0}}, {{0, 0}, {1/16, 1/4}, {1/8, 3/8}, {3/16, 1/2}, {1/4, 1/2}, {5/16, 5/8}, {3/8, 5/ 8}, {7/16, 5/8}, {1/2, 1/2}, {9/16, 5/8}, {5/8, 5/8}, {11/16, 5/ 8}, {3/4, 1/2}, {13/16, 1/2}, {7/8, 3/8}, {15/16, 1/4}, {1, 0}}}

Source: Borut Levart [http : // demonstrations.wolfram.com/TakagiCurve/ ]

Answer 3

Not sure if this counts, but this Pari GP implementation works for any x. 53 bytes

s(x)=abs(x-round(x)); bm(x)=sum(i=0,50,s(2^i*x)/2^i);

Answer 4

JavaScript (ES6), 35 bytes

B=x=>x%1?B(2*x%1)/2+(x<1/2?x:1-x):0

A straightforward implementation of this recursive formula.

Answer 5

Mathcad, 73 "bytes"

The Mathcad worksheet shown here defines the triangle function s(x) and the blancmange function (blanc(x) - but deemed to be just b(x) for golfing purposes). It also presents two variants, one specialized for rational numbers with power of two divisors, and one specialized for number of iterations of the summation. The worksheet also presents plots of the various blancmange functions and tables of their results.

The blancmange function works in both numeric (IEEE floating point) and symbolic (arbitrary arithmetic) modes.

Mathcad uses a virtual 2D worksheet on which the user places text or executable expressions (eg, formula or programs). Mathcad saves its worksheets in an XML format, which means that even a small program can be many hundreds or thousands of text characters long. For the purposes of code golfing, I take a Mathcad "byte" to mean the number of distinct symbols that the user must enter to create a program.

For example, to evaluate an expression, the user types "="; Mathcad will place an evaluation operator on the worksheet, which gives the appearance of an "=" sign bounded by two black box symbols (known as placeholders). Writing an expression in the left hand placeholder will cause Mathcad to evaluate the expression and put the result in the right hand placeholder. If the expression is a simple variable, "a" say, that contains a value, then from an user perspective this would count as 2 byte program "a" and "=". Raising one number to the power of another comprises entering the exponent operator (^) and then entering the two numbers in the appropriate placeholders. So, 3^4 would be a 3 byte program.