21
1
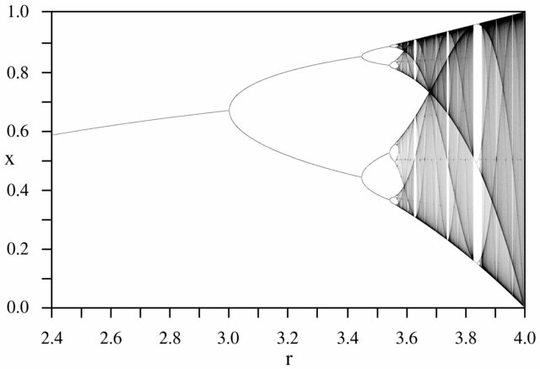
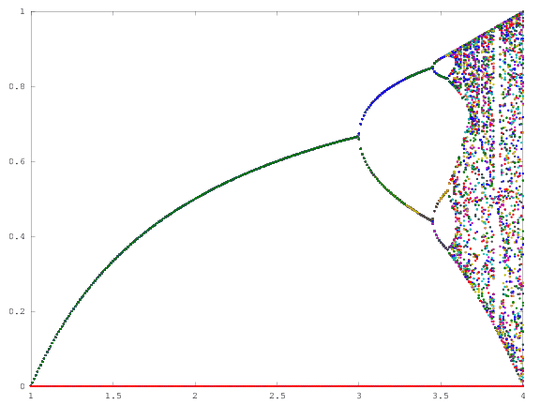
The purpose of the challenge is to approximately plot the attractor of the logistic map as a function of its parameter r (also called bifurcation diagram), or a subregion of it. The appearance of the graph can be seen in the following image from Wikipedia:
Background
The logistic map is a mathematical function that takes an input xk and maps it to an output xk+1 defined as
xk+1 = r xk (1−xk)
where r is the parameter of the map, assumed to lie in the interval [0, 4].
Given r in [0,4], and an initial value x0 in the interval [0,1], it is interesting to repeatedly apply the function for a large number N of iterations, producing a final value xN. Note that xN will necessarily lie in [0,1] too.
As an example, consider r = 3.2, N = 1000. The initial value x0 = 0.01 gives x1000 = 0.5130. For x0 = 0.02 the result is x0 = 0.7995. For any other initial values x0 the final values x1000 are extremely close to either 0.5130 or 0.7995. This is seen in the graph as the height of the two lines at horizontal position r = 3.2.
This does not mean that for r = 3.2 each sequence converges to one of those two values. In fact, for the two initial values considered above, the sequences are (note the oscillating behaviour):
x0 = 0.01, ..., x1000 = 0.5130, x1001 = 0.7995, x1002 = 0.5130, ...
x0 = 0.02, ..., x1000 = 0.7995, x1001 = 0.5130, x1002 = 0.7995, ...
What is true is that for sufficiently large N, and for almost all initial values x0, the term xN will be close to one of the elements of the set {0.5130, 0.7995}. This set is called the attractor for this specific r.
For other values of the parameter r the size of the atractor set, or its elements, will change. The graph plots the elements in the attractor for each r.
The attractor for a specific r can be estimated by
- testing a wide range of initial values x0;
- letting the system evolve for a large number N of iterations; and
- taking note of the final values xN that are obtained.
The challenge
Inputs
N: number of iterations.
r1, r2 and s. These define the set R of values of r, namely R = {r1, r1 + s, r1 + 2 s, ..., r2}.
Procedure
The set X of initial values x0 is fixed: X = {0.01, 0.02, ..., 0,99}. Optionally, 0 and 1 may also be included in X.
For each r in R and each x0 in X, iterate the logistic map N times to produce xN. Record the obtained tuples (r, xN).
Output
Plot each tuple (r, xN) as a point in the plane with r as horizontal axis and xN as vertical axis. Output should be graphic (not ASCII art).
Additional rules
- The indicated procedure defines the required result, but is not enforced. Any other procedure that procudes the same set of (r, xN) tuples can be used.
- Input is flexible as usual.
- Floating point errors won't be held against the answerer.
- Graphic output is required, in any of the accepted formats. In particular, output may be displayed on screen, or a graphics file may be produced, or an array of RGB values may be output. If outputting a file or an array, please post an example of what it looks like when displayed.
- Graphics may be vector or raster. For raster graphics, the size of the image should be at least 400×400 pixels.
- Each point should be shown as a single pixel, or as a mark with size of the order of one pixel (otherwise the graph quickly gets cluttered).
- Axis range should be [0,4] for r (horizontal axis) and [0,1] for xN (vertical axis); or it may be smaller as long as it includes all obtained points.
- Axis scales are arbitrary. In particular, the scale need not be the same for both axes.
- Grid lines, axis labels, colors and similar elements are acceptable, but not required.
- Shortest code in bytes wins.
Test cases
Click on each image for a high-resolution version.
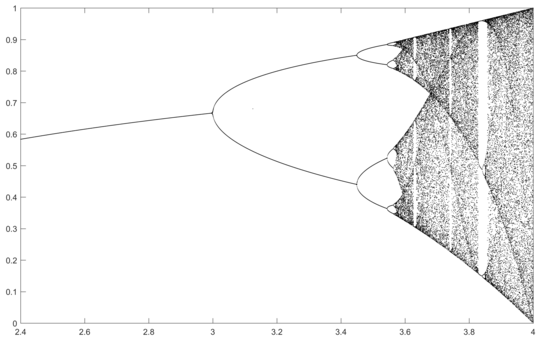
N = 1000; r1 = 2.4; r2 = 4; s = 0.001;
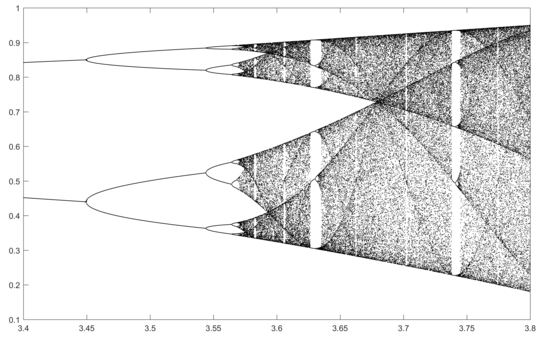
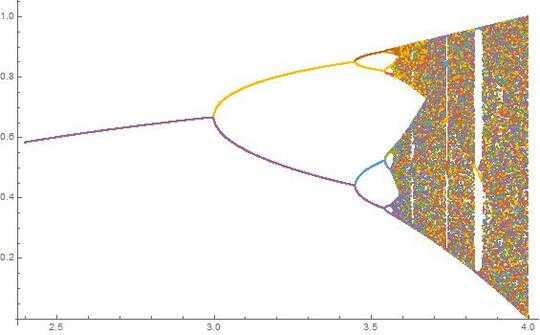
N = 2000; r1 = 3.4; r2 = 3.8; s = 0.0002;
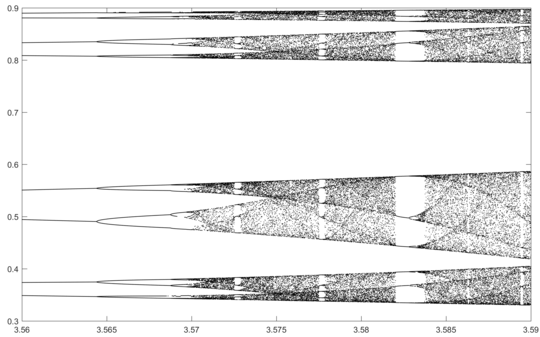
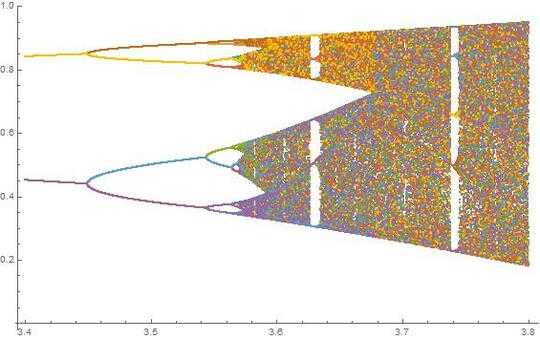
N = 10000; r1 = 3.56; r2 = 3.59; s = 0.00002;
Acknowledgment
Thanks to @FryAmTheEggman and @AndrasDeak for their helpful comments while the challenge was in the sandbox.
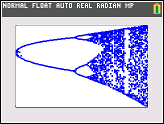
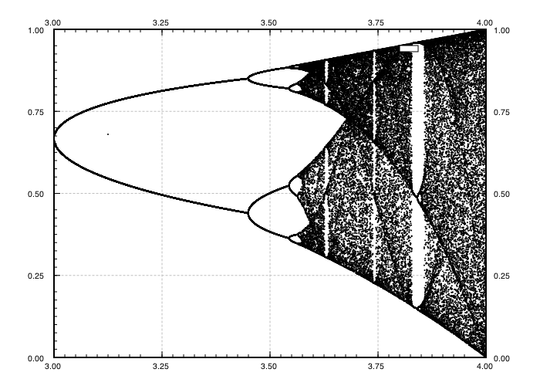
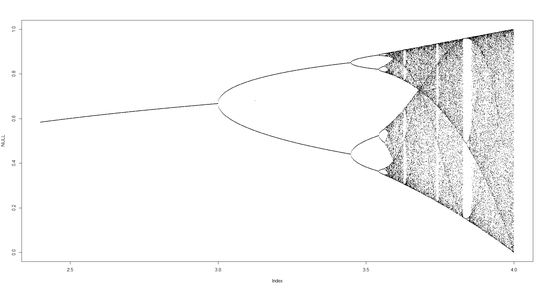
What no python solution?! – None – 2017-06-26T05:35:37.283
@Lembik I have a reference implementation in Python (and in Matlab), but I don't want to answer myself – Luis Mendo – 2017-06-26T07:34:16.043
You are allowed to answer your own questions on PPCG (perhaps surprisingly). – None – 2017-06-26T07:35:03.427
@Lembik I know, but I'd rather have others' answers – Luis Mendo – 2017-06-26T07:36:33.663