Manufactoria: generate the slowest possible accepting program

18

1

Write a Manufactoria program that will accept the empty input tape. But don't do it quickly! I mean, write the program quickly, but don't let it run quickly. The slower the program, the better, as long as it terminates eventually. The example program below takes 3:51 (the "total time" reported by the simulator).

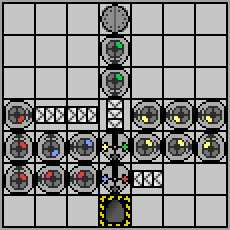
enter image description here

http://pleasingfungus.com/Manufactoria/?lvl=36&code=g12:5f3;r9:8f1;p12:9f3;c13:9f0;r11:9f0;r10:9f0;r9:9f1;b11:8f0;b10:8f1;r9:7f2;c10:7f2;c11:7f2;c12:7f3;q12:8f3;y13:8f2;y14:8f2;y15:8f1;y15:7f0;y14:7f0;y13:7f0;g12:6f3;&ctm=Slow_Accepter!;Generate_the_slowest_possible_accepting_machine;:;7;3;0;

Your program starts with the empty tape. It must doodle around a bit, but eventually reach the output square. You may leave data on the tape if you wish. The slowest program on the 7x7 Manufactoria board wins!

Your right arrow key is your friend, it speeds up the simulator.

Bonus points for crashing the simulator!

Keith Randall

Posted 2013-07-12T05:31:55.517

Reputation: 19 865

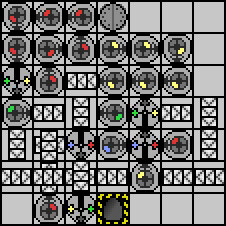
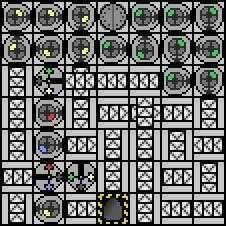
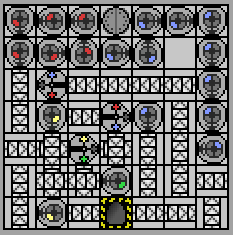
So there's no requirements for accepting/rejecting input other than the empty tape? – Volatility – 2013-07-12T05:34:45.627

@Volatility: correct. – Keith Randall – 2013-07-12T05:39:02.607

Annoyingly, the simulator won't report the running time unless the tape is empty at the end, since it doesn't match the challenge's expected output. (Luckily it was easy for me to erase the tape at the end without needing too much extra space.) – breadbox – 2013-07-15T13:05:08.777

Answers

22

~1023 iterations ~1015 iterations ~108 iterations

Manufactoria setup

http://pleasingfungus.com/Manufactoria/?lvl=32&code=g9:7f2;b12:8f2;p13:8f5;p11:8f3;r14:8f0;q11:10f3;q13:7f1;y13:9f1;r10:10f1;c12:9f2;c9:9f2;i11:9f7;i10:9f4;c9:8f3;i10:8f2;c14:9f0;c15:9f0;c15:8f3;c15:7f3;c14:7f2;g12:7f0;c11:7f3;c10:7f2;q9:6f7;r10:6f1;r9:5f3;c11:6f0;r10:5f2;r11:5f1;r9:4f3;r10:4f0;r11:4f0;y12:5f2;y13:5f2;y14:5f3;y14:6f0;y13:6f0;y12:6f0;&ctm=Slow_Accepter!;Generate_the_slowest_possible_accepting_machine;:;7;3;0;

The machine is basically an odometer running in base three, using the red, blue and yellow symbols to stand for the digits 0, 1, and 2 respectively. The green symbol is used to mark the end of the number. At the start, the tape is initialized with 49 red symbols. This is done by the parts in the top three rows of the machine. The bottom four rows handle the task of incrementing the number in a loop. On each iteration, the two branch cells on left-hand side work out how to apply the increment to current number, and then the branch cells on the right-hand side copy the remaining, unaffected digits.

Previously I've tried to estimate the machine's running time, were it allowed to run to completion, but at this level it makes more sense to just go by the number of iterations. Roughly speaking, it takes about a minute to complete one iteration -- but even if it took a second that would only decrease the running time by a single order of magnitude.

breadbox

Posted 2013-07-12T05:31:55.517

Reputation: 6 893

@breadbox, can you explain how this ends? It looks like when you count up to YYY...YG you will copy the whole Y string, leaving GYY..., then copy G back to the end for YYY...YG again, and just repeat that forever. Don't you need GG to end this? – Devon Parsons – 2015-01-14T18:14:04.780

Not that it matters, but you can extend the main loop by a fraction by making the bottom right conveyor take the longer path available – Devon Parsons – 2015-01-14T18:17:28.057

I figured out how it ends myself. After GYY.. the green gets bumped to the end, and all Ys get converted to Rs by the bottom left. Now G is at the front again, and it fails the B/R test, and finally gets bumped to the end. – Devon Parsons – 2015-01-14T18:27:05.747

4Ok, I give up.. – Volatility – 2013-07-15T22:21:40.370

2Don't give up! I've no doubt that this is still just scratching the surface. For example, compacting the odometer logic by merely one or two cells would allow an order-of-magnitude increase in running time. – breadbox – 2013-07-15T22:48:15.207

Wow. I knew there must be some way to get a huge time, but my brain has no hope of inventing this. – Igby Largeman – 2013-07-15T23:53:29.023

Very much like I had. I was able to pack the binary circuit a bit differently, might save a spot or two: – Keith Randall – 2013-07-17T00:57:39.643

1http://pleasingfungus.com/Manufactoria/?lvl=37&code=p10:10f5%3Br11:10f0%3Bb9:10f2%3Bg9:9f2%3Bi10:9f3%3Bp11:9f2%3Bb11:8f3%3Bq10:8f1%3Bc9:8f3%3By12:5f2%3By13:5f1%3By13:4f2%3By14:4f2%3By15:4f3%3By15:5f3%3By15:6f3%3Bc15:7f0%3Bq14:7f4%3Bb14:8f0%3Bb13:8f3%3Bb13:9f3%3Bb13:10f2%3Bb14:10f2%3Bb15:10f1%3Bb15:9f1%3Bc15:8f1%3Bc13:7f0%3Bc12:7f0%3Bc11:7f0%3Bc10:7f0%3Bc9:7f3%3Bc12:9f3%3B&ctm=Slow_Accepter%21%3BGenerate_the_slowest_possible_accepting_machine%3B:%3B7%3B3%3B0; – Keith Randall – 2013-07-17T00:58:06.707

I'm trying really hard to fight the urge to delete my answer. – Igby Largeman – 2013-07-17T08:29:55.733

5If it helps, I've often submitted golf answers that were way behind the leader, just because it was a different approach. One of the things I love about this site is that it preserves the diversity of responses. – breadbox – 2013-07-18T02:24:58.587

Dang, your result is almost the best one could possibly do, being equivalent to 3^50 iterations. – Simply Beautiful Art – 2017-10-22T22:23:58.973

1@SimplyBeautifulArt One could conceivably improve by having pairs of symbols be the digits (in which case you could use 15 out of 16 rather than 3 out of 4). Of course, you would run into a lot of difficulty with the small board size in trying to implement that. – feersum – 2017-10-23T03:52:14.040

8

603:25

Online test

I was re-reading through the Manufactoria questions today, and suddenly had an idea which would dramatically slow down the process: instead of just having 50 values and changing colours 3 times, the new program does that, but then after that, it decrements the number of values by 1, and goes through the colour-changing again, until there is an empty tape at which time the program stops.

The queue won't store any more than 50 values at one time, so there's no use trying to push too many values onto the tape - they just get pushed off straight away. As before, the conveyor belts aim to maximise the time taken for the thing to run. In fact, there was minimal tweaking down to achieve a tremendous increase in run-time.

Still nowhere near breadbox's answer though.

Volatility

Posted 2013-07-12T05:31:55.517

Reputation: 3 206

Interesting how similar our solutions are. We both started with a 9x6 multiplier, and we put the branch and x6 group in the same place! Yours is more elegant though - you used every cell and finished with a clean tape. – Igby Largeman – 2013-07-14T23:15:02.720

5

33:33

Worked on this for quite a while (Volatility set the bar pretty high), but once I hit 33:33, I thought it was a neat time to stop at.

The strategy is pretty blunt: basically fill up the tape with one colour, then another, then another, and always try to traverse as many cells as possible between each write (or group of writes).

I'm sure there are ways to be found that we can go a lot further with this.

Busy Beaver

Level link

Igby Largeman

Posted 2013-07-12T05:31:55.517

Reputation: 353

+1 I'll see what I can do to beat it ;) (although I'll probably not gonna get too far) – Volatility – 2013-07-14T21:40:41.637

Asked: 2013-07-12T05:31:55.517

Viewed: 1 109 times

Active: 2015-01-14T09:08:11.883