Linear interpolation of the Fibonacci sequence

Question

Your task is to find the n^th Fibonacci number, but n is not necessarily an integer.

The Fibonacci sequence, 0-indexed, goes as follows:

0, 1, 2, 3, 4, 5,  6,  7, ...

1, 1, 2, 3, 5, 8, 13, 21, ...

However, what happens if we want the 2.4^th number?

The 2.4^th number is 0.4 times the difference between the 3^rd and 2^nd Fibonacci numbers plus the 2^nd Fibonacci number. So, the 2.4^th Fibonacci number is 2 + 0.4 * (3 – 2) = 2.4.

Similarly, the 6.35^th Fibonacci number is 13 + 0.35 * (21 – 13) = 15.8.

Your task is to find the n^th Fibonacci number, such that n is greater than or equal to 0.

You may do this zero- or one-indexed, just please say which one you are using.

This is code-golf, so shortest code in bytes wins!

Some more examples:

0        1
4.5    6.5
0.7      1
7       21

Answer 1

Jelly, 5 bytes

_Ḟ1+¡

This is an iterative solution without built-ins. It uses the same indexing as the challenge spec.

Try it online!

Background

Let f be the function defined in the challenge spec and F the Fibonacci function defined as usual (i.e., with F(0) = 0). For a non-negative integer n, we have f(n) = F(n + 1). When 0 ≤ x < 1, the challenge spec defines f(n + x) as f(n) + (f(n + 1) - f(n))x.

Clearly, this just affects the base cases, but not the recursive formula, i.e., f(n) = f(n - 1) + f(n - 2) holds as it would for F. This means we can simplify the definition for non-integer arguments to the easier f(n) = f(n) + f(n - 1)x.

As others have noted in their answers, the recursive relationship also holds for non-integer arguments. This is easily verifiable, as

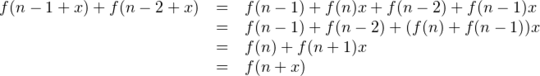
Since f(0) = f(1) = 1, f in constant in the interval [0, 1] and f(0 + x) = 1 for all x. Furthermore, f(-1) = F(0) = 0, so f(-1 + x) = f(-1) + (f(0) - f(-1))x = 0 + 1x = x. These base cases cover in [-1, 1), so together with the recursive formula, they complete the definition of f.

How it works

As before, let n + x be the only argument of our monadic program.

¡ is a quick, meaning that it consumes some links to its left and turns them into a quicklink. ¡ in particular consumes either one or two links.

• <F:monad|dyad><N:any> calls the link N, returning r, and executes F a total of r times.

• <nilad|missing><F:monad|dyad> sets r to the last command-line argument (or an input from STDIN in their absence) and executes F a total of r times.

Since 1 is a nilad (a link without arguments), the second case applies, and +¡ will execute + n times (a non-integer argument is rounded down). After each call to +, the left argument of the quicklink is replaced with the return value, and the right argument with the previous value of the left argument.

As for the entire program, Ḟ floors the input, yielding n; then _ subtract the result from the input, yielding **x, which becomes the return value.

1+¡ then calls +¡ – as described before – with left argument 1 = f(0 + x) and right argument x = f(-1 + x), which computes the desired output.

Answer 2

Mathematica, 32 bytes

If[#<2,1~Max~#,#0[#-1]+#0[#-2]]&

Pure function taking a nonnegative real number as input and returning a real number. If 1~Max~# were replaced by 1, this would be the standard recursive definition of the 0-indexed Fibonacci numbers for integer arguments. But 1~Max~# is the correct piecewise linear function for real inputs between 0 and 2, and the recursion takes care of the rest. (Trivia fact: changing this to the 1-indexed Fibonacci numbers can be accomplished simply by changing the Max to a Min!)

The shortest I could get with the builtin is the 37-byte (b=Fibonacci)[i=Floor@#](#-i)+b[i+1]&.

Answer 3

JavaScript (ES6), 30 bytes

f=x=>x<1?1:x<2?x:f(x-1)+f(x-2)

<input type=number value=2.4 oninput="O.value=f(value)"> <input id=O value=2.4 disabled>

Trivial modification of the zero-indexed recursive Fibonacci sequence definition. May give slight rounding errors for some inputs.

Answer 4

Python 2, 42 bytes

f=lambda n:n<3and max(1,n)or f(n-1)+f(n-2)

Try it online!

Answer 5

Jelly, 17 12 bytes

’Ñ+Ñ
’»0‘ÇỊ?

Try it online!

Non-builtin solution.

Explanation

Helper function 1Ŀ

’Ñ+Ñ
 Ñ    Call the main program on
’       {the input} - 1;
   Ñ  Call the main program on {the input};
  +   Add those results{and return the result}

Main program

’»0‘ÇỊ?
’        Subtract 1
 »0      but replace negative results with 0
     Ị?  If the result is less than or equal to 1
   ‘     Return the result plus 1
    Ç    else return the result

An input in the range 0 to 1 will therefore saturated-subtract to 0, thus we add 1 to get F(0)=F(1)=1. An input in the range 1 to 2 will return itself. Those base cases are sufficient to do a typical Fibonacci recursion and calculate the other values from there.

Answer 6

JavaScript (ES6), 67 64 bytes

Has a few issues with rounding

n=>(i=(g=(z,x=1,y=0)=>z?g(--z,x+y,x):y)(++n|0))+n%1*(g(++n|0)-i)

---

Try It

f=
n=>(i=(g=(z,x=1,y=0)=>z?g(--z,x+y,x):y)(++n|0))+n%1*(g(++n|0)-i)
console.log(f(2.4))
console.log(f(6.35))
console.log(f(42.42))

Answer 7

Excel, 137 124 119 113 102 97 Bytes

Non-recursive/iterative approach. (Directly calculate the nth terms) This uses the one-indexed method. Adding +1 to =TRUNC(B1) changes it to zero-indexed.

=A7+(A8-A7)*MOD(B1,1)
=5^.5
=(1+A2)/2
=TRUNC(B1)
=A4+1
=-1/A3
=(A3^A4-A6^A4)/A2
=(A3^A5-A6^A5)/A2

The code snippet is intended to be placed starting in cell A1.

The input cell is B1. The output cell is A1.

Answer 8

Jelly, 13 9 bytes

,‘ḞÆḞḅ%1$

This uses the same indexing as the challenge spec.

Try it online!

Background

Per the spec, we have F(n + x) = F(n) + (F(n + 1) - F(n))x, for natural n and 0 &leq; x < 1. Since F(n + 1) = F(n) + F(n - 1), this can be rewritten as F(n + x) = F(n) + F(n - 1)x.

Furthermore, the indexing used in the challenge spec defines a function f(n) = F(n + 1) (where F is the usual Fibonacci function, i.e., F(0) = 0), so we get the formula f(n + x) = F(n + 1) + F(n)x.

How it works

,‘ḞÆḞḅ%1$  Main link. Argument: n + x

 ‘         Increment; yield n + 1 + x.
,          Pair; yield [n + x, n + 1 + x].
  Ḟ        Floor; yield [n, n + 1].
   ÆḞ      Fibonacci; yield [F(n), F(n + 1)].
      %1$  Modulus 1; yield (n + x) % 1 = x.
     ḅ     Unbase; yield F(n)x + F(n + 1).

Answer 9

PHP, 90 Bytes

for($f=[1,1];$i<$a=$argn;)$f[]=$f[+$i]+$f[++$i];echo$f[$b=$a^0]+($a-$b)*($f[$b+1]-$f[$b]);

Online Version

Answer 10

Perl 6,  48  38 bytes

48

{$/=(1,1,*+*...*)[$_,$_+1];$0+($_-.Int)*($1-$0)}

Try it

38

sub f(\n){3>n??max 1,n!!f(n-1)+f(n-2)}

Try it

Expanded:

48

{
  $/ =          # store here so we can use $0 and $1
  (
    1,1,*+*...* # Fibonacci sequence
  )[
    $_,         # get the value by using floor of the input
    $_ + 1      # and get the next value
  ];

    $0            # the first value from above
  +
    ( $_ - .Int ) # the fractional part of the input
  *
    ( $1 - $0 )   # the difference between the two values in the sequence
}

($0 and $1 is short for $/[0] and $/[1])

38

sub f (\n) {
    3 > n           # if n is below 3
  ??
    max 1, n        # return it if it is above 1, or return 1
                    # if it was below 1, the answer would be 1
                    # the result for numbers between 1 and 3
                    # would be the same as the input anyway
  !!
    f(n-1) + f(n-2) # the recursive way to get a fibonacci number
}

This was inspired by other Python, and Javascript solutions

Answer 11

Julia 0.5, 31 bytes

This is basically just Rod's answer translated.

f(n)=n<3?max(1,n):f(n-1)+f(n-2)

Try it online!