25
4
Write a self-contained program which when given a polynomial and a bound will find all real roots of that polynomial to an absolute error not exceeding the bound.
Constraints
I know that Mathematica and probably some other languages have a one-symbol solution, and that's boring, so you should stick to primitive operations (addition, subtraction, multiplication, division).
There is certain flexibility on the input and output formats. You may take input via stdin or command-line arguments in any reasonable format. You may allow floating point or require that some representation of rational numbers be used. You may take the bound or the reciprocal of the bound, and if you're using floating point you may assume that the bound will not be less than 2 ulp. The polynomial should be expressed as a list of monomial coefficients, but it may be big- or little-endian.
You must be able to justify why your program will always work (modulo numerical issues), although it's not necessary to supply full proofs inline.
The program must handle polynomials with repeated roots.
Example
x^2 - 2 = 0 (error bound 0.01)
Input could be e.g.
-2 0 1 0.01
100 1 0 -2
1/100 ; x^2-2
Output could be e.g.
-1.41 1.42
but not
-1.40 1.40
as that has absolute errors of about 0.014...
Test cases
Simple:
x^2 - 2 = 0 (error bound 0.01)
x^4 + 0.81 x^2 - 0.47 x + 0.06 (error bound 10^-6)
Multiple root:
x^4 - 8 x^3 + 18 x^2 - 27 (error bound 10^-6)
Wilkinson's polynomial:
x^20 - 210 x^19 + 20615 x^18 - 1256850 x^17 + 53327946 x^16 -1672280820 x^15 +
40171771630 x^14 - 756111184500 x^13 + 11310276995381 x^12 - 135585182899530 x^11 +
1307535010540395 x^10 - 10142299865511450 x^9 + 63030812099294896 x^8 -
311333643161390640 x^7 + 1206647803780373360 x^6 -3599979517947607200 x^5 +
8037811822645051776 x^4 - 12870931245150988800 x^3 + 13803759753640704000 x^2 -
8752948036761600000 x + 2432902008176640000 (error bound 2^-32)
NB This question was in the Sandbox for approximately 3 months. If you think it needed improving before posting, visit the Sandbox and comment on the other proposed questions before they are posted on Main.
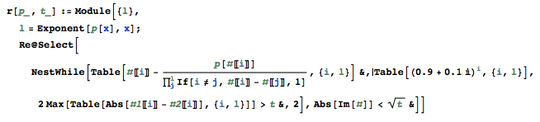
I know this is an old challenge, so don't feel obliged to answer if you don't feel like reopening it. (a) Can we write a function, or only a full program? (b) In case we can write a function, can we assume that the input uses some convenient data type, e.g., Python's
fractions.Fraction(a rational type)? (c) Do we have to handle polynomials of degree <1? (d) Can we assume that the leading coefficient is 1? – Ell – 2015-12-16T09:30:25.653(e) With regard to polynomials with repeated roots, it's worth making a distinction between roots of odd and even multiplicities (the test cases only have roots of odd multiplicities.) While roots of odd multiplicity are not too hard to deal with, I'm not sure how tangible it is to correctly handle roots of even multiplicity numerically, especially since you only specify an error margin for the values of the roots, not for their existence. (...) – Ell – 2015-12-16T09:30:37.213
(...) Since roots of even multiplicity only do a "touch and go" with the x-axis, if p is a polynomial with a root r of even multiplicity, then p + c has a different number of roots, for an arbitrarily small constant c (either r disappears, or it turns into two roots); so, to reliably determine if there's even a root at r, we pretty much have to pinpoint it. I think numerical solutions can only be more, or less, biased toward assuming there is, or there isn't, a root there, within some range of error. – Ell – 2015-12-16T09:30:45.373
@Ell, a) Full program. c) No, since they either have 0 roots or an infinite number. d) No, although it's a good point that I'm missing test cases. e) This might be a strong push towards using rationals rather than floating point, at least for an initial step of reduction to square-free polynomials. – Peter Taylor – 2015-12-16T09:53:23.930
My 100 point bounty was just thrown away. Wonderful. – lirtosiast – 2015-12-23T22:57:44.987
"You must be able to justify why your program will always work" Just in case someone needs help with that – Dr. belisarius – 2013-05-16T04:08:21.090
1@belisarius, ?? – Peter Taylor – 2013-05-16T07:20:04.397
3was intended as a joke :( – Dr. belisarius – 2013-05-16T11:57:09.023