8
1
Background
By expanding and cancelling terms, it is easy to show the following identity:
However, it is an open problem whether all 1/n-by-1/(n+1) rectangles can tile the unit square.
The Task
Your program should take a positive integer N as input in any convenient manner, and pack all 1/n-by-1/(n+1) open rectangles with n between 1 and N inclusive into the unit square, such that no two overlap.
For each rectangle you must generate the following integers in order:
- 1 if the horizontal edges are longer than the vertical edges, else 0
- The numerator and denominator of the x-coordinate of the bottom-left corner
- The numerator and the denominator of the y-coordinate of the bottom-left corner
Note that we take the unit square to be (0, 1) x (0, 1), with x-values running from left to right, and y-values running from bottom to top.
The final expected output is the concatenation of these integers for each rectangle in order of increasing n, in any convenient format (e.g. printed to stdout, or as a list returned from a function).
Example Input and Output
Input:
3
Output:
0 0 1 0 1 1 1 2 0 1 1 1 2 1 3
This parses as the following:
0 (0/1, 0/1) 1 (1/2, 0/1) 1 (1/2, 1/3)
Scoring
This is a code-golf challenge, so the answer with the fewest bytes wins. However, your algorithm should also be reasonably efficient; it should be able to run for all N<=100 in a total of around 10 minutes.
Your solution must give valid solutions for all N<=100, but provably complete algorithms are also welcome even if they aren't the shortest.
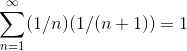
Seeing as this is an open problem, is there a cap on the largest value of $N$ for which our algorithm must be guaranteed to work? – Greg Martin – 2017-03-28T19:29:00.010
@GregMartin you should successfully run your program for N from 1 to 20. Brownie points if your algorithm can be proven to either succeed or disprove the conjecture. – user1502040 – 2017-03-28T19:33:23.867
For N≤20 the output can just be hardcoded ... is it your intention to allow that? There is a simple published algorithm that allows at least N=1,000,000,000.... – Greg Martin – 2017-03-28T19:37:25.590
OK, I changed the threshold from 20 to 100. – user1502040 – 2017-03-28T19:45:34.843
Oh, Goodness. I have not yet learnt sum to infinity, thus I do not understand this at all. – Matthew Roh – 2017-03-29T13:09:30.420
@SIGSEGV This isn't really a Riemann sum (there's no x or Δx). It's just the infinite series (1/1)(1/2) + (1/2)(1/3) + (1/3)(1/4) + ... which equals 1/2 + 1/6 + 1/12 + .... See series, and integral. Looking at the Partial sum formula of the integral, you can see that as m => ∞ that the result is 1.
– mbomb007 – 2017-04-04T21:05:17.187@user1502040 Can you perhaps add a graphical picture of your example? I think that'd help. – mbomb007 – 2017-04-04T21:18:08.227
@mbomb007 Oh no. Calculus. I didn't learn that too. – Matthew Roh – 2017-04-04T23:05:32.877