Escape a chessboard

Question

You find yourself on a chessboard, as one does. You can see the exit but it is awfully far away and you would rather not walk all the way. Luckily some locals have offered you a ride. A Knight, a Rook, a Bishop and a King are all willing to take you to your destination, but seeing how this is a chessboard they must each abide by the rules of chess on the way to your destination. You would like to get out of here as soon as possible, whose offer do you accept?

Task

Given a arbitrarily shaped and sized chessboard and two points on the chess board, output the chess piece that can move between the two locations in as few moves as possible. Boards will not necessarily be continuous meaning that there could be gaps between sections of the board. Each of the four pieces (King, Rook, Knight, and Bishop) can move according to their standard rules in chess. The Queen and pawn pieces have been intentionally left out of this challenge.

I/O

You may take input in any reasonable format and you may output in whatever format you choose as well. Your input and output must be self-consistent. If multiple pieces can make it to the destination in the same number of moves you must output all of the pieces that can get there in the minimum amount of time. If none of the four pieces can make it to the end you may output anything as long as it is distinct from all other possible outputs. This could include outputting nothing or throwing an error.

Test Cases

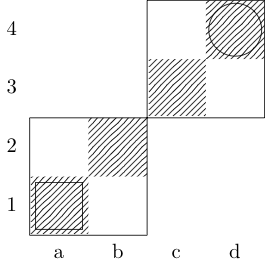
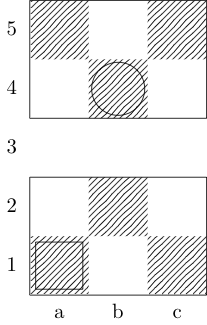
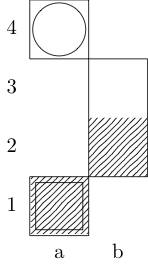
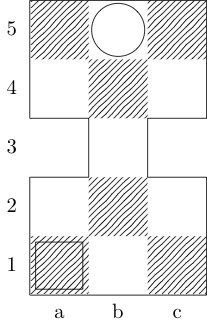
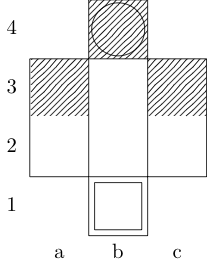
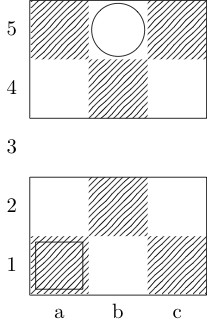
A square indicates the starting point and a circle indicates the ending point.

---

Bishop

---

Knight

---

King

---

Rook

---

King, Knight

---

None

Answer 1

Haskell, 447 439 437 432 bytes

t=[1,2]
p=[(+),(-)]
f=filter
a=abs
(#)=elem
x?y=[min x y..max x y]
f&g=(\x->g x>>=f)
(b!1)(c,r)=f(#b)[(c!d,r#s)|(!)<-p,(#)<-p,d<-t,s<-t,d/=s]
(b!2)(c,r)=f(\(d,s)->(c==d&&all(#b)[(c,z)|z<-r?s])||r==s&&all(#b)[(z,r)|z<-c?d])b
(b!3)(c,r)=f(\(d,s)->a(c-d)==a(r-s)&&all(#b)(zip(c?d)$r?s))b
(b!4)(c,r)=f(\(d,s)->a(c-d)<2&&a(r-s)<2)b
(b%p)n s=[s]>>=foldr(&)(:[])(replicate n$b!p)
g b s e=head$f(not.null)[[p|p<-[1..4],e#(b%p)n s]|n<-[0..]]

Call using g <board> <start> <end> where <board> :: [(Int, Int)], <start> :: (Int, Int) and <end> :: (Int, Int). Returns a list containing 1 for Knight, 2 for Rook, 3 for Bishop, and 4 for King. If no solutions are found, it consistently overflows the stack (that counts as throwing an error, right?).

Inspiration taken from LYAH's chapters on Monads—(%) is just a generalized and golfed inMany, with (&) equivalent to (Control.Monad.<=<). Everything else should be more-or-less self-explanatory.

This can probably be golfed a lot more, but I've had enough fun for now.

Ungolfed:

data Piece = Knight | Rook | Bishop | King deriving (Show)
type Place = (Int, Int)
type Board = [Place]

x `to` y = [min x y..max x y]

f <=< g = (\x -> g x >>= f)

moves
    :: Board    -- available spaces
    -> Piece    -- type of piece
    -> Place    -- starting place
    -> [Place]  -- places available in one move
moves b Knight (c,r) =
    filter (`elem` b) [(c!d, r#s) |
                       (!) <- [(+),(-)], (#) <- [(+),(-)],
                       d <- [1,2], s <- [1,2], d/=s]
moves b Rook   (c,r) =
    filter (\(d,s) -> (c == d && all (`elem` b) [(c,z) | z <- r `to` s])
                    || r == s && all (`elem` b) [(z,r) | z <- c `to` d]) b
moves b Bishop (c,r) =
    filter (\(d,s) -> abs(c-d) == abs(r-s)
                && all (`elem` b) (zip (c `to` d) (r `to` s))) b
moves b King   (c,r) =
    filter (\(d,s) -> abs(c-d) <= 1 && abs(r-s) <= 1) b

canGoIn
    :: Board    -- available spaces
    -> Piece    -- type of piece
    -> Int      -- number of moves
    -> Place    -- starting place
    -> [Place]  -- places available in the specified number of moves
canGoIn b p n s =
    return s >>= foldr (<=<) return (replicate n (moves b p))

quickestPieces
    :: Board    -- available spaces
    -> Place    -- starting place
    -> Place    -- ending place
    -> [Piece]  -- quickest pieces
quickestPieces b s e =
        head $ filter (not.null)
            [[p | p <- [Knight, Rook, Bishop, King], elem e (canGoIn b p n s)] |
                n<-[0..]]

Answer 2

Mathematica, 326 325 bytes

Thanks to masterX224 for pointing out a byte savings!

f[g_,w_,x_]:=(c={{1,1},{-1,1}};s=c.c/2;e=#<->#2&@@@#&;j=Join;h=FindShortestPath;t=#~Tuples~2&;a@d_:=e@Select[t@g,#-#2&@@#==d&];y@k=j@@(a/@j[s,c]);y@n=j@@(a/@{{1,2},{2,1},{-2,1},{-1,2}});v=Flatten[e@t@#&/@ConnectedComponents@a@#&/@#]&;y@r=v@s;y@b=v@c;Pick[p={b,k,n,r},z=Length[h[y@#,w,x]/.h@__->0]&/@p,Min[z~Complement~{0}]]);

Defines a function f taking three arguments: g is a list of ordered pairs of integers representing the board, and w and x ordered pairs representing the start and end squares. The output is the subset of {b, k, n, r} (representing bishop, king, knight, and rook, respectively) which have a minimal-moves path between the two squares. For example, the third test case is invoked by f[{{0, 0}, {1, 1}, {1, 2}, {0, 3}}, {0, 0}, {0, 3}] and returns {k}; the last two test cases return {k, n} and {}, respectively.

The strategy is to translate the squares of the board into vertices of a graph, where the edges are determined by each piece's moves, and then use built-in graph routines.

More user-friendly version of the code:

 1  f[g_, w_, x_] := ( c = {{1, 1}, {-1, 1}}; s = c.c/2;
 2    e = # <-> #2 & @@@ # &; j = Join; h = FindShortestPath; t = #~Tuples~2 &; 
 3    a@d_ := e@Select[t@g, # - #2 & @@ # == d &]; 
 4    y@k = j @@ (a /@ j[s, c]); 
 5    y@n = j @@ (a /@ {{1, 2}, {2, 1}, {-2, 1}, {-1, 2}}); 
 6    v = Flatten[e@t@# & /@
 7         ConnectedComponents@a@# & /@ #] &;
 8    y@r = v@s; y@b = v@c; 
 9    Pick[p = {b, k, n, r}, 
10      z = Length[h[y@#, w, x] /. h@__ -> 0] & /@ p, 
11      Min[z~Complement~{0}]]
12  );

In line 3, Select[g~Tuples~2, # - #2 & @@ # == d finds all ordered pairs of vertices whose difference is the vector d; e then transforms each such ordered pair into an undirected graph edge. So a is a function that creates edges between all vertices that differ by a fixed vector.

That's enough to define, in lines 4 and 5, the king's graph y@k (which takes the union of edges generated by the vectors {1, 1}, {-1, 1}, {0, 1}, and {-1, 0}) and the knight's graph y@n (which does the same with {1, 2}, {2, 1}, {-2, 1}, and {-1, 2}).

In line 7, ConnectedComponents@a@# takes one of these neighbor graphs and then finds its connected components; this corresponds to grouping all line segments of vertices in the given direction (so that a rook or bishop doesn't have to move through them one by one). Then e@t@# on line 6 puts edges between every pair of vertices in the same connected component, which are then Flattened into a single graph. Thus lines 6 through 8 define the rook's graph y@r and the bishop's graph y@b.

Finally, lines 9 through 11 choose the elements of {b, k, n, r} that yield the shortest path between the two target vertices. FindShortestPath will throw an error and return unevaluated if a target vertex doesn't appear in the graph (which will happen if no edges emanate from it), so we use h@__ -> 0 to return 0 in those cases instead. And the lack of a path between valid vertices returns a list of length 0, so Min[z~Complement~{0}] calculates the length of the smallest path that actually exists, ignoring the bad cases above.