Perl + Math::{ModInt, Polynomial, Prime::Util}, score ≤ 92819
$m=Math::Polynomial;sub l{($n,$b,$d)=@_;$n||$d||return;$n%$b,l($n/$b,$b,$d&&$d-1)}sub g{$p=$m->interpolate([grep ref$_[$_],0..$map{$p->evaluate($_)}0..$}sub p{prev_prime(128**$s)}sub e{($_,$r)=@_;length||return'';$s=$r+1;s/^[␀␁]/␁$&/;@l=map{mod($_,p$s)}l(Math::BigInt->from_bytes($_),p$s);$@l+$r>p($s)&&return e($_,$s);$a=0;join'',map{map{chr$_+$a}l($_->residue,128,$s,($a^=128))}g(@l)}sub d{@l=split/([␀-␡]+)/,$_[0];@l||return'';$s=vecmax map length,@l;@l=g map{length==$s&&mod($m->new(map{ord()%128}split//)->evaluate(128),p$s)}@l;$$_=$m->new(map{$_->residue}@l)->evaluate(p$s)->to_bytes;s/^␁//;$_}
Control pictures are used to represent the corresponding control character (e.g. ␀ is a literal NUL character). Don't worry much about trying to read the code; there's a more readable version below.
Run with -Mbigint -MMath::ModInt=mod -MMath::Polynomial -MNtheory=:all. -MMath::Bigint=lib,GMP is not necessary (and thus not included in the score), but if you add it before the other libraries it'll make the program run somewhat faster.
Score calculation
The algorithm here is somewhat improvable, but would be rather harder to write (due to Perl not having the appropriate libraries). Because of this, I made a couple of size/efficiency tradeoffs in the code, on the basis that given that bytes can be saved in the encoding, there's no point in trying to shave off every point from golfing.
The program consists of 600 bytes of code, plus 78 bytes of penalties for command-line options, giving a 678 point penalty. The rest of the score was calculated by running the program on the best-case and worst-case (in terms of output length) string for every length from 0 to 99 and every radiation level from 0 to 9; the average case is somewhere in between, and this gives bounds on the score. (It's not worth trying to calculate the exact value unless another entry comes in with a similar score.)
This therefore means that the score from encoding efficiency is in the range 91100 to 92141 inclusive, thus the final score is:
91100 + 600 + 78 = 91778 ≤ score ≤ 92819 = 92141 + 600 + 78
Less-golfed version, with comments and test code
This is the original program + newlines, indentation, and comments. (Actually, the golfed version was produced by removing newlines/indentation/comments from this version.)
use 5.010; # -M5.010; free
use Math::BigInt lib=>'GMP'; # not necessary, but makes things much faster
use bigint; # -Mbigint
use Math::ModInt 'mod'; # -MMath::ModInt=mod
use Math::Polynomial; # -MMath::Polynomial
use ntheory ':all'; # -Mntheory=:all
use warnings; # for testing; clearly not necessary
### Start of program
$m=Math::Polynomial; # store the module in a variable for golfiness
sub l{ # express a number $n in base $b with at least $d digits, LSdigit first
# Note: we can't use a builtin for this because the builtins I'm aware of
# assume that $b fits into an integer, which is not necessarily the case.
($n,$b,$d)=@_;
$n||$d||return;
$n%$b,l($n/$b,$b,$d&&$d-1)
}
sub g{ # replaces garbled blocks in the input with their actual values
# The basic idea here is to interpolate a polynomial through all the blocks,
# of the lowest possible degree. Unknown blocks then get the value that the
# polynomial evaluates to. (This is a special case of Reed-Solomon coding.)
# Clearly, if we have at least as many ungarbled blocks as we did original
# elements, we'll get the same polynomial, thus we can always reconstruct
# the input.
# Note (because it's confusing): @_ is the input, $_ is the current element
# in a loop, but @_ is written as $_ when using the [ or # operator (e.g.
# $_[0] is the first element of @_.
# We waste a few bytes of source for efficiency, storing the polynomial
# in a variable rather than recalculating it each time.
$p=$m->interpolate([grep ref$_[$_],0..$#_],[grep ref,@_]);
# Then we just evaluate the polynomial for each element of the input.
map{$p->evaluate($_)}0..$#_
}
sub p{ # determines maximum value of a block, given (radiation+1)
# We split the input up into blocks. Each block has a prime number of
# possibilities, and is stored using the top 7 bits of (radiation+1)
# consecutive bytes of the output. Work out the largest possible prime that
# satisfies this property.
prev_prime(128**$s)
}
sub e{ # encoder; arguments: input (bytestring), radiation (integer)
($_,$r)=@_; # Read the arguments into variables, $_ and $r respectively
length||return''; # special case for empty string
$s=$r+1; # Also store radiation+1; we use it a lot
# Ensure that the input doesn't start with NUL, via prepending SOH to it if
# it starts with NUL or SOH. This means that it can be converted to a number
# and back, roundtripping correctly.
s/^[␀␁]/␁$&/; #/# <- unconfuse Stack Exchange's syntax highlighting
# Convert the input to a bignum, then to digits in base p$s, to split it
# into blocks.
@l=map{mod($_,p$s)}l(Math::BigInt->from_bytes($_),p$s);
# Encoding can reuse code from decoding; we append $r "garbled blocks" to
# the blocks representing the input, and run the decoder, to figure out what
# values they should have.
$#l+=$r;
# Our degarbling algorithm can only handle at most p$s blocks in total. If
# that isn't the case, try a higher $r (which will cause a huge increase in
# $b and a reduction in @l).
@l+$r>p($s)&&return e($_,$s);
# Convert each block to a sequence of $s digits in base 128, adding 128 to
# alternating blocks; this way, deleting up to $r (i.e. less than $s) bytes
# will preserve the boundaries between each block; then convert that to a
# string
$a=0; # we must initialize $a to make this function deterministic
join'',map{map{chr$_+$a}l($_->residue,128,$s,($a^=128))}g(@l)
}
sub d{ # decoder: arguments; encdng (bytestring)
# Reconstruct the original blocks by looking at their top bits
@l=split/([␀-␡]+)/,$_[0];
@l||return''; # special case for empty string
# The length of the longest block is the radiation parameter plus 1 (i.e.
# $s). Use that to reconstruct the value of $s.
$s=vecmax map length,@l;
# Convert each block to a number, or to undef if it has the wrong length.
# Then work out the values for the undefs.
@l=g map{
# Convert blocks with the wrong length to undef.
length==$s&&
# Convert other blocks to numbers, via removing any +128 and then
# using Math::Polynomial to convert the digit list to a number.
mod($m->new(map{ord()%128}split// #/# <- fix syntax highlighting
)->evaluate(128),p$s)
}@l;
# Remove the redundant elements at the end; now that they've reconstructed
# the garbled elements they have no further use.
$#l-=$s-1;
# Convert @l to a single number (reversing the conversion into blocks.)
$_=$m->new(map{$_->residue}@l)->evaluate(p$s)
# Convert that number into a string.
->to_bytes;
# Delete a leading SOH.
s/^␁//; #/# <- unconfuse Stack Exchange's syntax highlighting
# Finally, return the string.
$_
}
### Testing code
use Encode qw/encode decode/;
# Express a string using control pictures + IBM437, to make binary strings
# easier for a human to parse
sub format_string {
($_)=@_;
$_ = decode("Latin-1", $_);
s/[\0-\x1f]/chr (0x2400 + ord $&)/eag;
s/\x7f/chr 0x2421/eag;
s/[ -~\x80-\xff]/decode("IBM437",$&)/eag;
encode("UTF-8","\x{ff62}$_\x{ff63}")
}
sub test {
my ($string, $radiation, $samples) = @_;
say "Input: ", format_string($string);
my $encoding = e($string, $radiation);
say "Encoding: ", format_string($encoding);
say "Input length ", length($string), ", encoding length ", length($encoding), ", radiation $radiation";
my $decoding = d($encoding);
$decoding eq $string or die "Mistake in output!";
say "Decoding: ", format_string($decoding), " from ",
format_string($encoding);
# Pseudo-randomly generate $samples radiation-damaged versions.
srand 1;
for my $i (1..$samples) {
my $encdng = $encoding;
for my $r (1..$radiation) {
substr $encdng, int(rand(length $encdng)), 1, "";
}
my $newdecoding = d($encdng);
say "Decoding: ", format_string($newdecoding), " from ",
format_string($encdng);
$newdecoding eq $string or die "Mistake in output!";
}
say "";
length $encoding;
}
test "abcdefghijklm", 1, 10;
test "abcdefghijklm", 2, 10;
test "abcdefghijklm", 5, 10;
test "abcdefghijklm", 10, 10;
test "\0\0\0\0\0", 1, 10;
test "\5\4\3\2\1", 2, 10;
test "a", 10, 10;
my %minlength = ();
my %maxlength = ();
for my $length (0..99) {
my ($min, $max) = ("", "");
$length and ($min, $max) =
("\2" . "\0" x ($length - 1), "\1" . "\377" x ($length - 1));
for my $radiation (0..9) {
$minlength{"$length-$radiation"} = test $min, $radiation, 1;
$maxlength{"$length-$radiation"} = test $max, $radiation, 1;
}
}
say "Minimum score: ", vecsum values %minlength;
say "Maximum score: ", vecsum values %maxlength;
Algorithm
Simplifying the problem
The basic idea is to reduce this "deletion coding" problem (which is not a widely-explored one) into an erasure coding problem (a comprehensively explored area of mathematics). The idea behind erasure coding is that you're preparing data to be sent over an "erasure channel", a channel that sometimes replaces the characters it sends with a "garble" character that indicates a known position of an error. (In other words, it's always clear where corruption has occurred, although the original character is still unknown.) The idea behind that is pretty simple: we divide the input up into blocks of length (radiation + 1), and use seven out of the eight bits in each block for data, whilst the remaining bit (in this construction, the MSB) alternates between being set for an entire block, clear for the entire next block, set for the block after that, and so on. Because the blocks are longer than the radiation parameter, at least one character from each block survives into the output; so by taking runs of characters with the same MSB, we can work out which block each character belonged to. The number of blocks is also always greater than the radiation parameter, so we always have at least one undamaged block in the encdng; we thus know that all blocks that are longest or tied for longest are undamaged, allowing us to treat any shorter blocks as damaged (thus a garble). We can also deduce the radiation parameter like this (it's the length of an undamaged block, minus 1).
Erasure coding
As for the erasure coding part of the problem, this uses a simple special case of the Reed-Solomon construction. This is a systematic construction: the output (of the erasure coding algorithm) is equal to the input plus a number of extra blocks, equal to the radiation parameter. We can calculate the values needed for these blocks in a simple (and golfy!) way, via treating them as garbles, then running the decoding algorithm on them to "reconstruct" their value.
The actual idea behind the construction is also very simple: we fit a polynomial, of the minimum possible degree, to all the blocks in the encoding (with garbles interpolated from the other elements); if the polynomial is f, the first block is f(0), the second is f(1), and so on. It's clear that the degree of the polynomial will equal the number of blocks of input minus 1 (because we fit a polynomial to those first, then use it to construct the extra "check" blocks); and because d+1 points uniquely define a polynomial of degree d, garbling any number of blocks (up to the radiation parameter) will leave a number of undamaged blocks equal to the original input, which is enough information to reconstruct the same polynomial. (We then just have to evaluate the polynomial to ungarble a block.)
Base conversion
The final consideration left here is to do with the actual values taken by the blocks; if we do polynomial interpolation on the integers, the results may be rational numbers (rather than integers), much larger than the input values, or otherwise undesirable. As such, instead of using the integers, we use a finite field; in this program, the finite field used is the field of integers modulo p, where p is the largest prime less than 128radiation+1 (i.e. the largest prime for which we can fit a number of distinct values equal to that prime into the data part of a block). The big advantage of finite fields is that division (except by 0) is uniquely defined and will always produce a value within that field; thus, the interpolated values of the polynomials will fit into a block just the same way that the input values do.
In order to convert the input into a series of block data, then, we need to do base conversion: convert the input from base 256 into a number, then convert into base p (e.g. for a radiation parameter of 1, we have p = 16381). This was mostly held up by Perl's lack of base conversion routines (Math::Prime::Util has some, but they don't work for bignum bases, and some of the primes we work with here are incredibly large). As we're already using Math::Polynomial for polynomial interpolation, I was able to reuse it as a "convert from digit sequence" function (via viewing the digits as the coefficients of a polynomial and evaluating it), and this works for bignums just fine. Going the other way, though, I had to write the function myself. Luckily, it isn't too hard (or verbose) to write. Unfortunately, this base conversion means that the input is typically rendered unreadable. There's also an issue with leading zeroes; this program uses the simple (but not perfectly efficient) method of prepending a 1 octet to the program if it starts with a 0 or 1 octet (and reversing the translation when decoding), thus avoiding the issue altogether.
It should be noted that we can't have more than p blocks in the output (otherwise the indexes of two blocks would become equal, and yet possibly need to produce different outputs form the polynomial). This only happens when the input is extremely large. This program solves the issue in a very simple way: increasing radiation (which makes the blocks larger and p much larger, meaning we can fit much more data in, and which clearly leads to a correct result).
One other point worth making is that we encode the null string to itself, because the program as written would crash on it otherwise. It's also clearly the best possible encoding, and works no matter what the radiation parameter is.
Potential improvements
The main asymptotic inefficiency in this program is to do with the use of modulo-prime as the finite fields in question. Finite fields of size 2n exist (which is exactly what we'd want here, because the blocks' payload sizes are naturally a power of 128). Unfortunately, they're rather more complex than a simple modulo construction, meaning that Math::ModInt wouldn't cut it (and I couldn't find any libraries on CPAN for handling finite fields of non-prime sizes); I'd have to write an entire class with overloaded arithmetic for Math::Polynomial to be able to handle it, and at that point the byte cost might potentially overweigh the (very small) loss from using, e.g., 16381 rather than 16384.
Another advantage of using power-of-2 sizes is that the base conversion would become much easier. However, in either case, a better method of representing the length of the input would be useful; the "prepend a 1 in ambiguous cases" method is simple but wasteful. Bijective base conversion is one plausible approach here (the idea is that you have the base as a digit, and 0 as not a digit, so that each number corresponds to a single string).
Although the asymptotic performance of this encoding is very good (e.g. for an input of length 99 and a radiation parameter of 3, the encoding is always 128 bytes long, rather than the ~400 bytes that repetition-based approaches would get), its performance is less good on short inputs; the length of the encoding is always at least the square of the (radiation parameter + 1). So for very short inputs (length 1 to 8) at radiation 9, the length of the output is nonetheless 100. (At length 9, the length of the output is sometimes 100 and sometimes 110.) Repetition-based approaches clearly beat this erasure-coding-based approach on very small inputs; it might be worth changing between multiple algorithms based on the size of the input.
Finally, it doesn't really come up in the scoring, but with very high radiation parameters, using a bit of every byte (⅛ of the output size) to delimit blocks is wasteful; it would be cheaper to use delimiters between the blocks instead. Reconstructing the blocks from delimiters is rather harder than with the alternating-MSB approach, but I believe it to be possible, at least if the data is sufficiently long (with short data, it can be hard to deduce the radiation parameter from the output). That would be something to look at if aiming for an asymptotically ideal approach regardless of the parameters.
(And of course, there could be an entirely different algorithm that produces better results than this one!)
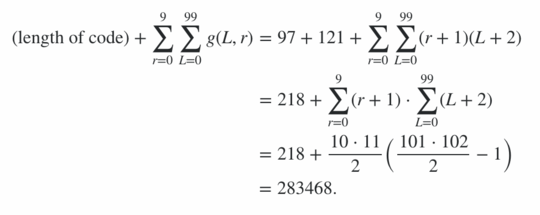
May the decoder know the radiation parameter as well? – orlp – 2017-02-23T06:54:39.717
(or length, but I believe that knowing either should give you the other for most schemes) – orlp – 2017-02-23T07:01:23.103
1@orlp: No, it only has the string. In a [tag:radiation-hardening] problem, the decoder (i.e. language) doesn't know the radiation rules used, so your decoder doesn't know them either; it has to deduce them from its input. – None – 2017-02-23T12:39:25.500
Based on this computerphile video I'd make a language that takes codels in 3-byte triplets: if they don't all match, something went wrong and we have enough information to figure out what the right value is. There's probably a way to do it with fewer bits but I don't have the brain to work out how at the moment.
– Draco18s no longer trusts SE – 2017-06-19T17:08:44.117How do you combine the header and the programs? – CalculatorFeline – 2017-06-19T19:43:07.917
@CalculatorFeline: If you're using the three-file approach, via whatever mechanism your language supports for including header files (e.g.
#includein C) or libraries (again in C, specifying the filename on the command line when building; note that that would incur a byte penalty). – None – 2017-06-19T19:44:37.357What if my language does not support any mechanism for including header files? – CalculatorFeline – 2017-06-19T19:46:27.570
@CalculatorFeline: Then use the 1-file or 2-file approach. The reason a range of possible approaches is given is to support a range of possible languages. – None – 2017-06-19T19:47:27.117