6
2
This is "programming" at its most fundamental.
Build a diagram of (two-wire) NAND logic gates that will take the input wires A1, A2, A4, A8, B1, B2, B4, B8, representing two binary numbers A to B from 0 to 15, and return values on the output wires C1, C2, C4, and C8 representing C, which is the sum of A and B modulo 16.
Your score is determined by the number of NAND gates (1 point per gate). To simplify things, you may use AND, OR, NOT, and XOR gates in your diagram, with the following corresponding scores:
NOT: 1AND: 2OR: 3XOR: 4
Each of these scores corresponds to the number of NAND gates that it takes to construct the corresponding gate.
Lowest score wins.
Updates:
03-07 19:09: Due to discussions with Jan Dvorak, it came to my attention that the total number of gates, constants and splits is always determined solely by the number of gates. Because of this, I have simplified the score requirement back down to simply the number of gates required.
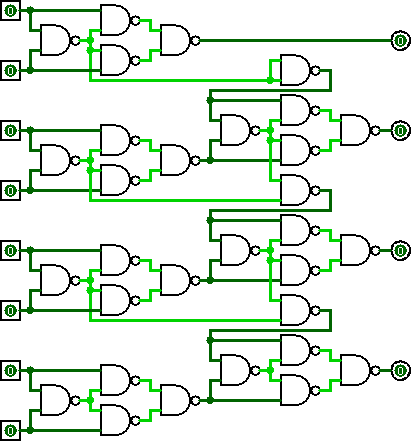
2
I don't think you can get much better than the classic full-adder design.
– Mr. Llama – 2013-03-07T20:52:58.327That uses AND, OR, and XOR gates and would have a score of 29 per digit (minus a few for carrying in the end cases). Can you condense it into using fewer NANDs? – Joe Z. – 2013-03-07T21:08:14.893
Are multi-wire NANDs allowed? – John Dvorak – 2013-03-07T21:14:44.217
@JanDvorak Not sure what a multi-wire NAND is. – Joe Z. – 2013-03-07T21:17:11.110
@JoeZeng NAND(X,Y,Z) = NOT(AND(X,AND(Y,Z))) – John Dvorak – 2013-03-07T21:18:18.707
They don't seem like a standard construction. I think I'd only allow them with the score it takes to build them out of two-wire NANDs and splits. – Joe Z. – 2013-03-07T21:26:13.427
1They are quite standard. It emits true if any input is false. – John Dvorak – 2013-03-07T21:26:54.580
I understand that. What I meant is that multi-wire logic gates in general don't seem to be typical of logic gate diagrams, so I don't think I would allow them as one unit with a special score. – Joe Z. – 2013-03-07T21:28:42.007
But, if you can construct a multi-wire NAND using only regular NANDs and splits, feel free to reuse that construction with its equivalent score. – Joe Z. – 2013-03-07T21:29:21.397