Python 3, 78 77 75 70 68 62 bytes
f=lambda n,k=3,m=1,j=0:k<n and-m%k*j*2/k+f(n,k+2,m*k**4,m%k/k)
Thanks to @xnor for golfing off 2 4 bytes and paving the way for 4 more!
Try it online!
Background
Recall that Wilson's theorem states that for all integers k > 1,

where a ≡ b (mod d) means that a - b is evenly divisible by d, i.e., a and b have the same residue when divided by d.
In Wilson Theorems for Double-, Hyper-, Sub- and Super-factorials, the authors prove generalizations for double factorials, on which this answer builds. The double factorial of an integer k ≥ 0 is defined by
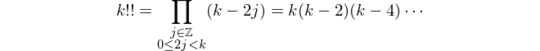
Theorem 4 of the aforementioned paper states the following.

Elevating both sides of the congruences to the fourth power, we deduce that

for all odd primes p. Since 1!! = 1, the equivalence holds also for p = 2.
Now, doing the same to Wilson's theorem reveals that

Since

it follows that

whenever p is prime.
Now, let k be an odd, positive, composite integer. By definition, there exist integers a, b > 1 such that k = ab.
Since k is odd, so are a and b. Thus, both occur in the sequence 1, 3, …, k - 2 and
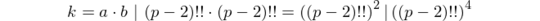
where | indicates divisibility.
Summing up, for all odd integers k > 1

where p(k) = 1 if k is prime and p(k) = 0 if k is composite.
How it works
When the function f is called with a single argument, k, m, and j are initialized as 3, 1, and 0.
Note that ((k - 2)!!)4 = 1!!4 = 1 = m. In fact, the equality m = ((k - 2)!!)4 will hold at all times. j is a float and will always be equal to ((k - 4)!!)4 % (k - 2) / (k - 2).
While k < n, the right argument of and will get evaluated. Since j = ((k - 4)!!)4 % (k - 2) / (k - 2), as proven in the first paragraph, j = 1/(k - 2) if k - 2 is prime and j = 0 if not. Likewise, since m % k = ((k - 2)!!)4 equals 1 if k is prime and 0 if not, -m % k = k - 1 if k is prime and -m % k = 0 if not. Therefore, -m%k*j*2/k evaluates to 2(k - 1)/(k(k - 2)) = ((k - 2) + k)/(k(k - 2)) = 1/k + 1/(k - 2) if the pair (k - 2, k) consists of twin primes and to 0 if not.
After computing the above, we add the result to the return value of the recursive call f(n,k+2,m*k**4,m%k/k). k gets incremented by 2 so it only takes odd values‡†, we multiply m by k4 since mk4 = ((k - 2)!!)4k4 = (k!!)4, and pass the current value of m % k / k – which equals 1/k if the "old" k is a prime and 0 if not – as parameter j to the function call.
Finally, once k is equal to or greater than n, f will return False and the recursion stops. The return value of f(n) will be the sum of all 1/k + 1/(k - 2) such (k - 2, k) is a twin prime pair and k < n, as desired.
‡ The results from the Background paragraph hold only for odd integers. Since even integers cannot be twin primes, we can skip them safely.

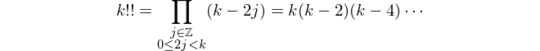





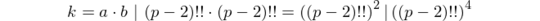

Can an exact fraction be output? – LegionMammal978 – 2017-01-22T00:58:01.830
@LegionMammal978 Yes, I'll clarify. – Mego – 2017-01-22T00:58:31.713
Side note: the value 1.902160583104... for Brun's constant is only conjectured; not even the first significant figure has been rigorously computed (that is, it's not even known whether it's greater than or less than 2). – Greg Martin – 2017-01-22T01:05:41.313
@GregMartin While that's true, it's also the best approximation we currently have. – Mego – 2017-01-22T01:06:46.390
5 is the only prime that appears in two prime pairs – Christian Sievers – 2017-01-22T03:41:05.213
@ChristianSievers My number theory is a bit rusty in places, so I opted for safe rather than sorry. :) – Mego – 2017-01-22T06:07:06.967
He's right though. All primes larger than 3 must be coprime with 6, so they're congruent to 1 or -1 modulo 6. If p, p+2, and p+4 are all prime, one of them is congruent to 3 modulo 6, which is only possible if one of them (p, to be precise) is equal to 3. – Dennis – 2017-01-22T06:09:55.310