34
4
Introduction
Similar to the Fibonacci Sequence, the Padovan Sequence (OEIS A000931) is a sequence of numbers that is produced by adding previous terms in the sequence. The initial values are defined as:
P(0) = P(1) = P(2) = 1
The 0th, 1st, and 2nd terms are all 1. The recurrence relation is stated below:
P(n) = P(n - 2) + P(n - 3)
Thus, it yields the following sequence:
1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, 21, 28, 37, 49, 65, 86, 114, 151, 200, 265, 351, ...
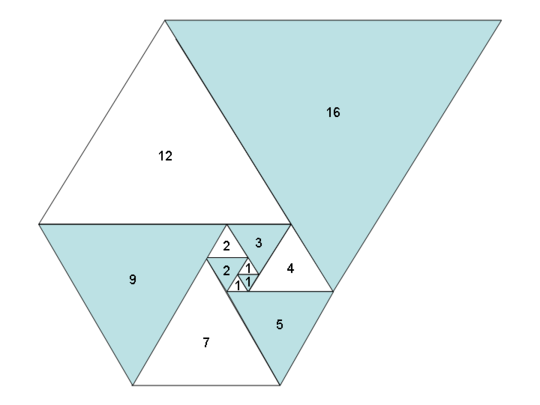
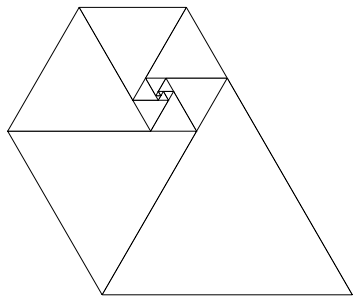
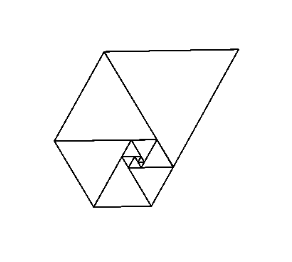
Using these numbers as side lengths of equilateral triangles yields a nice spiral when you place them all together, much like the Fibonacci Spiral:
Image courtesy of Wikipedia
Task
Your task is to write a program that recreates this spiral by graphical output, with input corresponding to which term.
Rules
- Your submission must be able to handle at least up to the 10th term (9)
- Your submission must be a full program or function that takes input and displays a graphical result (either outputs an image or graphs, etc)
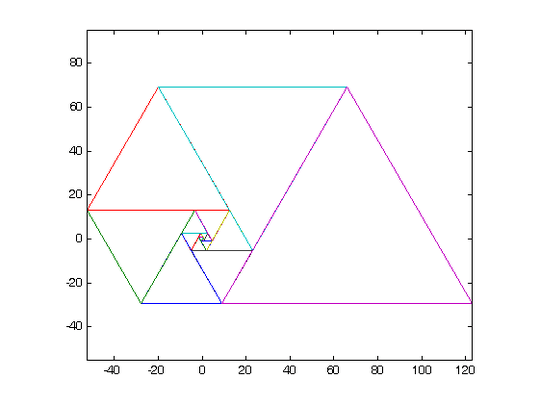
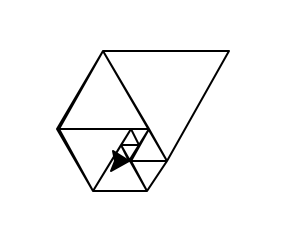
- You must show proof of your graphical output in your submission
- Rotations of the output are allowed, in 60 degree multiples, with the same representation
- Going counter-clockwise is also allowed
- Standard loopholes are forbidden
You may assume that input will be >0 and that correct format of input will be given.
Scoring
This is code-golf, so the shortest code in bytes wins. Happy New Years everyone!
Is trailing space after lines allowed? – Pavel – 2017-01-01T02:37:56.187
@Pavel Yes. Let me add that – Andrew Li – 2017-01-01T02:38:15.083
Does the output have to be identical to the example or are reflections and rotations (multiples of 60 degrees) allowed? – Level River St – 2017-01-01T03:28:34.587
@LevelRiverSt I would allow that. Let me clarify that in the post. – Andrew Li – 2017-01-01T03:30:13.930
I think this would also be interesting as a [graphical-output] challenge. – mbomb007 – 2017-01-01T20:22:33.667
@mbomb007 added option for graphical output. – Andrew Li – 2017-01-01T20:32:51.890
Is it allowed to mirror the output? – John Dvorak – 2017-01-01T22:32:56.557
@JanDvorak what do you mean by that? – Andrew Li – 2017-01-01T22:36:03.643
I mean, is it okay if my spiral grows counter-clockwise rather than clockwise like yours does? – John Dvorak – 2017-01-01T22:36:52.380
@JanDvorak Yes, that is allowed. Let me add that into the challenge – Andrew Li – 2017-01-01T22:37:38.143
3Not a fan of allowing both ASCII art and graphical output in the same challenge. They're very very different tasks, and mixing them together makes answers solving the two different possibilities completely incomparable. It would be better to have two separate challenges, one for ASCII art and one for graphical output. – Martin Ender – 2017-01-01T22:58:11.793
@MartinEnder Ok, sure. Since both of the answers here currently are graphical-output, I could have another challenge for ASCII. Would that be ok? – Andrew Li – 2017-01-01T23:01:48.187
@AndrewLi sounds good to me. – Martin Ender – 2017-01-01T23:05:45.890