23
5
This challenge is inspired by this fantastic animated diagram (thanks to flawr for posting it in chat).
Given an input n, draw all of its prime factors as nested polygons of dots, as specified.
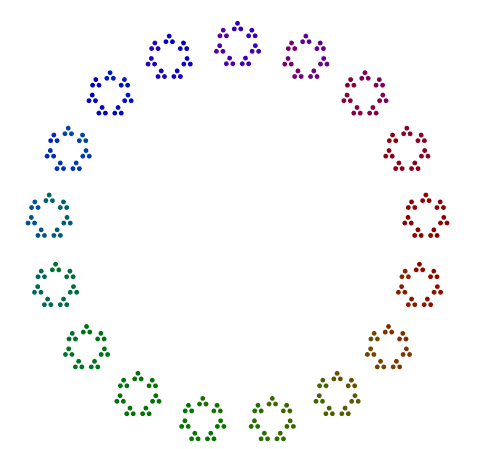
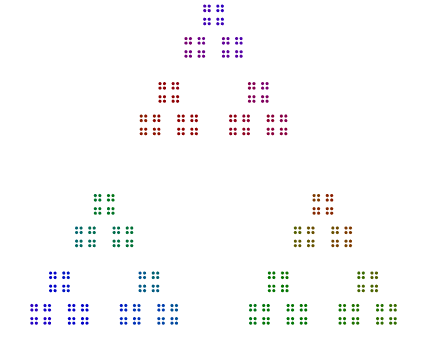
For example, given the number 357 = 17x7x3, you arrange 3 dots in a triangle, 7 versions of those triangles in a heptagon, and 17 versions of those heptagons in a 17-gon. In short, nested polygons going from the largest prime factor on the outside to the smallest on the inside. For 357, your answer should look a little like this (with or without color):
Every polygon of every prime >= 3 should not be rotated around the diagram.
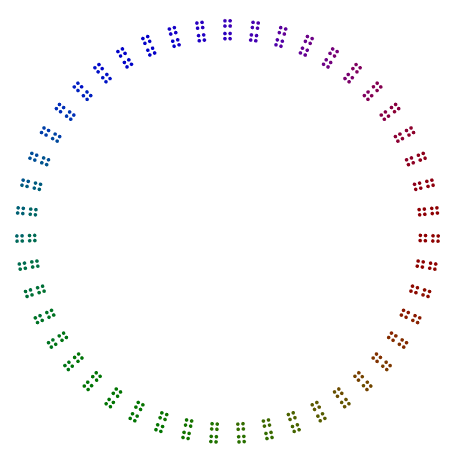
The only exception is the prime 2, specifically for odd powers of 2. As you can see in the example for 376 = 47x2x2x2 below, the 8s rotate and are not single lines of 2s, but are vertical stacks for 4s in a square. Even powers of 2, arranged in squares, do not need to be rotated in this way.
In fact, 448 = 7x2x2x2x2x2x2 has a diagram that looks like a heptagon of 64s, and 64 is arranged into a square of squares of squares, but without rotation.
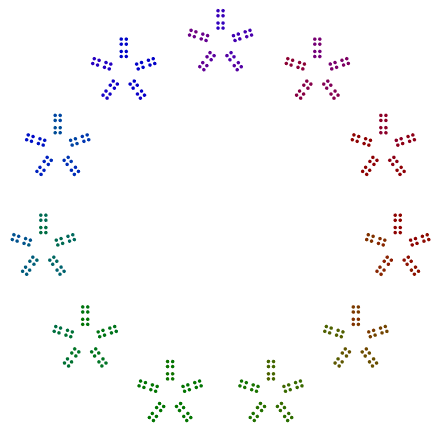
Two more examples are 440 = 11x5x2x2x2 and 432 = 3x3x3x2x2x2x2. We see that 440 with an odd power of 2, has rotated 8s, but 432 with an even power of 2 does not rotate its 16s.
And finally, here is a minimal example, 10 = 5x2, without color that I mocked up with Python and its turtle module.
The challenge
- Given an input
nwhere1 <= n <= 10000, output an image of its nested factor polygons. - Rules are:
- The image is made up of nested polygons of dots, from a polygon with (the largest prime factor) sides on the outside to the smallest prime factor on the inside.
- For the factor 2, the powers of 2 should stack as a line, then a squares, then a line of squares, and so on. Even powers of 2 should not be rotated. Odd powers of 2 should be rotated around their respective polygons, and they should be stacked vertically before rotation.
- You may orient the image however you like (though I prefer up), but every nested polygon should be facing the same direction as any other polygon with the sole exception of odd powers of 2.
- You have two options for image size and dot size:
- The image size is static and the dot size decreases as
nincreases (as in the animation). - The dot size is static and the image size grows as
nincreases.
- The image size is static and the dot size decreases as
- The first three layers of polygons should be distinguishable from neighboring polygons (i.e. not touching), but considering the size of the images at and around
n=10000, it's okay if the layers after start to touch. I'd prefer it if they didn't, but it may be unavoidable to fit on an image that is uploadable to Stack Exchange. - Color is optional.
- The shape of the dots is up to you. If squares are better for your language, use those.
- No bonuses, but I would like to see someone animate and color the diagrams like in the original post.
Thanks to Conor O'Brien, EasterlyIrk, Martin Ender, Kritixi Lithos, Mego, DJ McMayhem, and El'endia Starman for their help in writing this question.
This code golf, so shortest code wins. Good luck and good golfing!
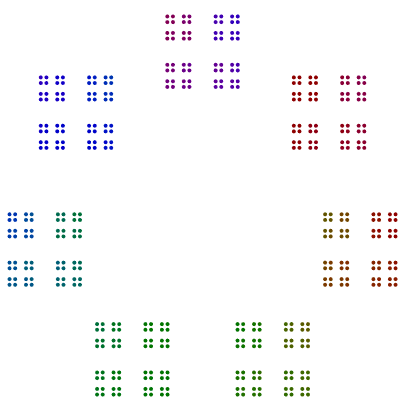

is
n = n //= isupposed to ben//= i? – Bobas_Pett – 2016-12-29T19:43:05.343@Bobas_Pett Nah, you're looking at the ungolfing/explanation, and that's supposed to say
n = n // i. I'll go fix it and add to the explanation while I'm at it. – Sherlock9 – 2016-12-30T04:05:41.950