Count the number of cyclic words in an input

Question

Cyclic Words

Problem Statement

We can think of a cyclic word as a word written in a circle. To represent a cyclic word, we choose an arbitrary starting position and read the characters in clockwise order. So, "picture" and "turepic" are representations for the same cyclic word.

You are given a String[] words, each element of which is a representation of a cyclic word. Return the number of different cyclic words that are represented.

Fastest wins (Big O, where n = number of chars in a string)

Answer 1

Python

Here's my solution. I think it might still be O(n²), but I think the average case is much better than that.

Basically it works by normalizing each string so that any rotation will have the same form. For example:

'amazing' -> 'mazinga'
'mazinga' -> 'mazinga'
'azingam' -> 'mazinga'
'zingama' -> 'mazinga'
'ingamaz' -> 'mazinga'
'ngamazi' -> 'mazinga'
'gamazin' -> 'mazinga'

The normalization is done by looking for the minimum character (by char code), and rotating the string so that character is in the last position. If that character occurs more than once, then the characters after each occurrence are used. This gives each cyclic word a canonical representation, that can be used as a key in a map.

The normalization is n² in the worst case (where every character in the string is the same, e.g. aaaaaa), but most of the time there's only going to be a few occurrences, and the running time will be closer to n.

On my laptop (dual core Intel Atom @ 1.66GHz and 1GB of ram), running this on /usr/share/dict/words (234,937 words with an average length of 9.5 characters) takes about 7.6 seconds.

#!/usr/bin/python

import sys

def normalize(string):
   # the minimum character in the string
   c = min(string) # O(n) operation
   indices = [] # here we will store all the indices where c occurs
   i = -1       # initialize the search index
   while True: # finding all indexes where c occurs is again O(n)
      i = string.find(c, i+1)
      if i == -1:
         break
      else:
         indices.append(i)
   if len(indices) == 1: # if it only occurs once, then we're done
      i = indices[0]
      return string[i:] + string[:i]
   else:
      i = map(lambda x:(x,x), indices)
      for _ in range(len(string)):                       # go over the whole string O(n)
         i = map(lambda x:((x[0]+1)%len(string), x[1]), i)  # increment the indexes that walk along  O(m)
         c = min(map(lambda x: string[x[0]], i))    # get min character from current indexes         O(m)
         i = filter(lambda x: string[x[0]] == c, i) # keep only the indexes that have that character O(m)
         # if there's only one index left after filtering, we're done
         if len(i) == 1:
            break
      # either there are multiple identical runs, or
      # we found the unique best run, in either case, we start the string from that
      # index
      i = i[0][0]
      return string[i:] + string[:i]

def main(filename):
   cyclic_words = set()
   with open(filename) as words:
      for word in words.readlines():
         cyclic_words.add(normalize(word[:-1])) # normalize without the trailing newline
   print len(cyclic_words)

if __name__ == '__main__':
   if len(sys.argv) > 1:
      main(sys.argv[1])
   else:
      main("/dev/stdin")

Answer 2

Python (3) again

The method I used was to calculate a rolling hash of each word starting at each character in the string; since it's a rolling hash, it takes O(n) (where n is the word length) time to compute all the n hashes. The string is treated as a base-1114112 number, which ensures the hashes are unique. (This is similar to the Haskell solution, but more efficient since it only goes through the string twice.)

Then, for each input word, the algorithm checks its lowest hash to see if it's already in the set of hashes seen (a Python set, thus lookup is O(1) in the set's size); if it is, then the word or one of its rotations has already been seen. Otherwise, it adds that hash to the set.

The command-line argument should be the name of a file that contains one word per line (like /usr/share/dict/words).

import sys

def rollinghashes(string):
    base = 1114112
    curhash = 0
    for c in string:
        curhash = curhash * base + ord(c)
    yield curhash
    top = base ** len(string)
    for i in range(len(string) - 1):
        curhash = curhash * base % top + ord(string[i])
        yield curhash

def cycles(words, keepuniques=False):
    hashes = set()
    uniques = set()
    n = 0
    for word in words:
        h = min(rollinghashes(word))
        if h in hashes:
            continue
        else:
            n += 1
            if keepuniques:
                uniques.add(word)
            hashes.add(h)
    return n, uniques

if __name__ == "__main__":
    with open(sys.argv[1]) as words_file:
        print(cycles(line.strip() for line in words_file)[0])

Answer 3

Mathematica

Decided to start again, now that I understand the rules of the game (I think).

A 10000 word dictionary of unique randomly composed "words" (lower case only) of length 3. In similar fashion other dictionaries were created consisting of strings of length 4, 5, 6, 7, and 8.

ClearAll[dictionary]      
dictionary[chars_,nWords_]:=DeleteDuplicates[Table[FromCharacterCode@RandomInteger[{97,122},
chars],{nWords}]];
n=16000;
d3=Take[dictionary[3,n],10^4];
d4=Take[dictionary[4,n],10^4];
d5=Take[dictionary[5,n],10^4];
d6=Take[dictionary[6,n],10^4];
d7=Take[dictionary[7,n],10^4];
d8=Take[dictionary[8,n],10^4];

gtakes the current version of dictionary to check. The top word is joined with cyclic variants (if any exist). The word and its matches are appended to the output list, out, of processed words. The output words are removed from the dictionary.

g[{wds_,out_}] := 
   If[wds=={},{wds,out},
   Module[{s=wds[[1]],t,c},
   t=Table[StringRotateLeft[s, k], {k, StringLength[s]}];
   c=Intersection[wds,t];
   {Complement[wds,t],Append[out,c]}]]

f runs through all words dictionary.

f[dict_]:=FixedPoint[g,{dict,{}}][[2]]

---

Example 1: actual words

r = f[{"teaks", "words", "spot", "pots", "sword", "steak", "hand"}]
Length[r]

{{"steak", "teaks"}, {"hand"}, {"pots", "spot"}, {"sword", "words"}}
4

---

Example 2: Artificial words. Dictionary of strings of length 3. First, timing. Then the number of cycle words.

f[d3]//AbsoluteTiming
Length[%[[2]]]

5402

---

Timings as a function of word length. 10000 words in each dictionary.

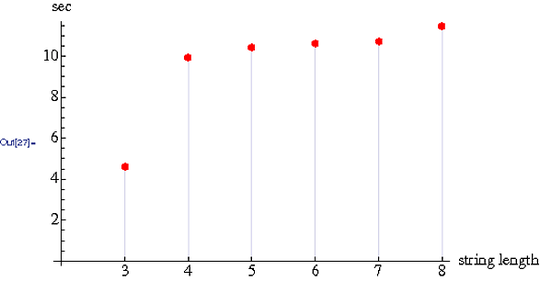
I don't particularly know how to interpret the findings in terms of O. In simple terms, the timing roughly doubles from the three character dictionary to the four character dictionary. The timing increases almost negligibly from 4 through 8 characters.

Answer 4

Haskell

Not sure about the efficiency of this, most likely rather bad. The idea is to first create all possible rotations of all the words, count the values that uniquely represent the strings and select the minimum. That way we get a number that is unique to a cyclic group.
We can group by this number and check the number of these groups.

If n is the number of words in the list and m is the length of a word then calculating the 'cyclic group number' for all the words is O(n*m), sorting O(n log n) and grouping O(n).

import Data.List
import Data.Char
import Data.Ord
import Data.Function

groupUnsortedOn f = groupBy ((==) `on` f) . sortBy(compare `on` f)
allCycles w = init $ zipWith (++) (tails w)(inits w)
wordval = foldl (\a b -> a*256 + (fromIntegral $ ord b)) 0
uniqcycle = minimumBy (comparing wordval) . allCycles
cyclicGroupCount = length . groupUnsortedOn uniqcycle

Answer 5

This can be done in O(n) avoiding quadratic time. The idea is to construct the full circle traversing the base string twice. So we construct "amazingamazin" as the full circle string to check all cyclic strings corresponding to "amazing".

Below is the Java solution:

public static void main(String[] args){
    //args[0] is the base string and following strings are assumed to be
    //cyclic strings to check 
    int arrLen = args.length;
    int cyclicWordCount = 0;
    if(arrLen<1){
        System.out.println("Invalid usage. Supply argument strings...");
        return;
    }else if(arrLen==1){
        System.out.println("Cyclic word count=0");
        return;         
    }//if

    String baseString = args[0];
    StringBuilder sb = new StringBuilder();
    // Traverse base string twice appending characters
    // Eg: construct 'amazingamazin' from 'amazing'
    for(int i=0;i<2*baseString.length()-1;i++)
        sb.append(args[0].charAt(i%baseString.length()));

    // All cyclic strings are now in the 'full circle' string
    String fullCircle = sb.toString();
    System.out.println("Constructed string= "+fullCircle);

    for(int i=1;i<arrLen;i++)
    //Do a length check in addition to contains
     if(baseString.length()==args[i].length()&&fullCircle.contains(args[i])){
        System.out.println("Found cyclic word: "+args[i]);
        cyclicWordCount++;
    }

    System.out.println("Cyclic word count= "+cyclicWordCount);
}//main

Answer 6

I don't know if this is very efficient, but this is my first crack.

private static int countCyclicWords(String[] input) {
    HashSet<String> hashSet = new HashSet<String>();
    String permutation;
    int count = 0;

    for (String s : input) {
        if (hashSet.contains(s)) {
            continue;
        } else {
            count++;
            for (int i = 0; i < s.length(); i++) {
                permutation = s.substring(1) + s.substring(0, 1);
                s = permutation;
                hashSet.add(s);
            }
        }
    }

    return count;
}

Answer 7

Perl

not sure i understand the problem, but this matches the example @dude posted in the comments at least. please correct my surely incorrect analysis.

for each word W in the given N words of the string list, you have to step through all characters of W in the worst case. i have to assume the hash operations are done in constant time.

use strict;
use warnings;

my @words = ( "teaks", "words", "spot", "pots", "sword", "steak", "hand" );

sub count
{
  my %h = ();

  foreach my $w (@_)
  {
    my $n = length($w);

    # concatenate the word with itself. then all substrings the
    # same length as word are rotations of word.
    my $s = $w . $w;

    # examine each rotation of word. add word to the hash if
    # no rotation already exists in the hash
    $h{$w} = undef unless
      grep { exists $h{substr $s, $_, $n} } 0 .. $n - 1;
  }

  return keys %h;
}

print scalar count(@words), $/;