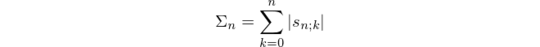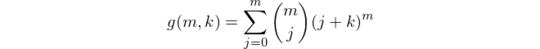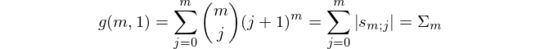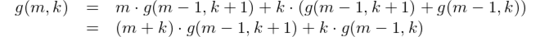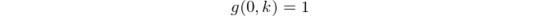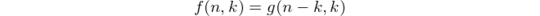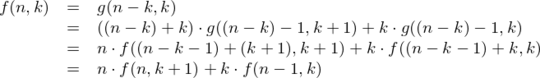Absolute Sums of Sidi Polynomial Coefficients

Question

Background

The Sidi polynomial of degree n – or the (n + 1)^th Sidi polynomial – is defined as follows.

The Sidi polynomials have several interesting properties, but so do their coefficients. The latter form OEIS sequence A075513.

Task

Write a full program or a function that, given a non-negative integer n, prints or returns the absolute sum of the coefficients of the Sidi polynomial of degree n, that is

These sums form OEIS sequence A074932.

If you prefer 1-based indexing, you can take a positive integer n instead and compute the absolute sum of the coefficients of the n^th Sidi polynomial.

Because this is code-golf, you must make your code as short as possible. All standard rules apply.

Test cases (0-based)

 n           Σ

 0           1
 1           3
 2          18
 3         170
 4        2200
 5       36232
 6      725200
 7    17095248
 8   463936896
 9 14246942336

Test cases (1-based)

 n           Σ

 1           1
 2           3
 3          18
 4         170
 5        2200
 6       36232
 7      725200
 8    17095248
 9   463936896
10 14246942336

Answer 1

05AB1E, 10 bytes

Ý©¹c®>¹m*O

Uses the CP-1252 encoding. Try it online!

Answer 2

Python 2, 43 bytes

f=lambda n,k=1:k/n or n*f(n,k+1)+k*f(n-1,k)

Try it online!

A different approach

Ever since I posted this challenge, I tried to come up with a recursive solution to this problem. While I failed using nothing more than pen and paper, I managed to turn the formula to golf into a practical problem – at least for certain definitions of practical – which made it easier to analyze.

Imagine a game show with k + m candidates that works as follows.

In round 1, all candidates have to accomplish a certain task as fast as they can. The k candidates that accomplish the task the fastest win 1 k$ (one kilodollar) each and advance to round 3.

In round 2, the m remaining candidates get a second chance to join the other k. Each candidate is asked a question. If they answer the question correctly, they win 1 k$ and advance to round 3. However, if they fail to answer the question, they are eliminated from the game. This means round 3 will have between k and k + m candidates, depending on how many can answer their questions.

Round 3 consists of m more contests that are similar to round 1. In each contest, the participants have to accomplish a certain task. Unlike round 1, only one candidate receives a prize, but all candidates get to participate in the next contest. Each contests pay twice as much as the contest before it; the first one pays 2 k$ and the last one 2^m k$.

Note that since all prizes are powers of two, knowing how much prize money a candidate earned means we know if they advanced to round 3 and which of the contests of round 3 they won.

Assume you're watching the game show and round 1 is already over, so you know which k candidates have already reached round 3 and which m candidates are still stuck in round 2. In how many ways can the remaining prize money be distributed?

Once we know which of the second round's m candidates have advanced to round 3, it's easy to calculate the possible outcomes for this specific scenario. If j candidates advance, there are k + j total candidates in round 3, and thus k + j possible outcomes for each contest. With m individual contests in round 3, this makes (k + j)^m outcomes for all m contests.

Now, j can take any value between 0 and m, depending on which candidates answer correctly in round 2. For each fix value of j, there are ^mC_j different combinations of j candidates that could have advanced to round 3. If we call the total number of possible outcomes for k round 3 candidates and m round 2 candidates g(m, k), we get the following formula.

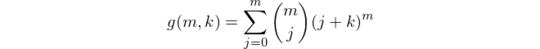
If we fix k = 1, we get the following special case, which constitutes our new approach to solve the original problem.

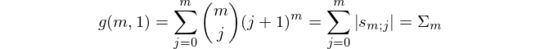
A recursive formula

Now, assume that you fell asleep during the commercials after round 1, and woke up just in time to see who won the last contest of round 3 and thus the grand prize of 2^m k$. You don't have any other information, not even how much prize money that candidate won in total. In how many ways can the remaining prize money be distributed?

If the winner was one of the m candidates of round 2, we already now that they must have advanced to round 3. Thus, we effectively have k + 1 candidates in round 3, but only m - 1 candidates in round 2. Since we know the winner of the last contest, there are only m - 1 contests with uncertain outcomes, so there are g(m - 1, k + 1) possible outcomes.

If the winner is one of the k candidates that skipped round 2, the calculation becomes slightly trickier. As before, there are only m - 1 rounds left, but now we still have k candidates in round 3 and m candidates in round 2. Since the number of round 2 candidates and the number of round 3 contests are different, the possible outcomes cannot be calculated with a simple invocation of g. However, after the first round 2 candidate has answered – rightly or wrongly – the number of round 2 candidates once again matches the m - 1 round 3 contests. If the candidate advances, there are k + 1 round 3 candidates and thus g(m - 1, k + 1) possible outcomes; if the candidate is eliminated, the number of round 3 candidates remains at k and there are g(m - 1, k) possible outcomes. Since the candidate either advances or not, there are g(m - 1, k + 1) + g(m - 1, k) possible outcomes combining these two cases.

Now, if we add the potential outcomes for all k + m candidates that could have won the grand prize, the result must match g(m, k). There are m round 2 contestants that lead to g(m - 1, k + 1) potential outcomes each, and k round 3 contestants that lead to g(m - 1, k + 1) + g(m - 1, k) ones. Summing up, we get the following identity.

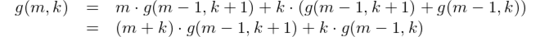
Together with the base case

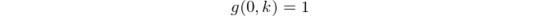
these two formulae characterize the function g completely.

A golfy implementation

While

g=lambda m,k=1:0**m or(m+k)*g(m-1,k+1)+k*g(m-1,k)

(49 bytes, 0**m yields 1 once m drops to 0) or even

g=lambda m,k=1:m<1 or(m+k)*g(m-1,k+1)+k*g(m-1,k)

(48 bytes, returns True instead of 1) would be valid solutions, there are still bytes to be saved.

If we define a function f that takes the number n of round 1 candidates instead of the number m of round 2 candidates as first argument, i.e.,

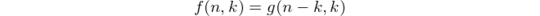
we get the recursive formula

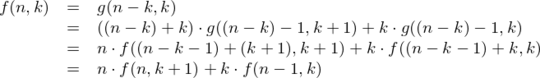
with base case

Finally, we have

so the Python implementation

f=lambda n,k=1:k/n or n*f(n,k+1)+k*f(n-1,k)

(k/n yields 1 once n = k) solves the task at hand with 1-based indexing.

Answer 3

Mathematica, 33 32 bytes

Saved one byte thanks to JungHwan Min.

Binomial[#,r=0~Range~#].(r+1)^#&

Answer 4

Pyth - 13 12 bytes

Just implements the formula without the (-1)^k part.

sm*.cQd^hdQh

Test Suite.

Answer 5

MATL, 12 bytes

t:XnG:QG^*sQ

Input is 0-based.

Try it online!

Explanation

Consider input 5 as an example.

t      % Take n implicitly. Duplicate
       % STACK: 5, 5
:      % Range [1 2 ...n]
       % STACK: 5, [1 2 3 4 5]
Xn     % N-choose-k, vectorized
       % STACK: [5 10 10 5 1]
G:Q    % Push [2 3 ... n+1]
       % STACK: [5 10 10 5 1], [2 3 4 5 6]
G^     % Raise to n
       % STACK: [5 10 10 5 1], [32 243 1024 3125 7776]
*      % Multiply, element-wise
       % STACK: [160 2430 10240 15625 7776]
s      % Sum of array
       % STACK: 36231
Q      % Add 1. Display implicitly
       % STACK: 36232

Answer 6

R, 36 bytes

sum(choose(n<-scan(),0:n)*(0:n+1)^n)

R's vectorization comes in handy here when applying the formula.

Answer 7

J, 19 bytes

+/@((!{:)*>:^{:)@i.

Uses one-based indexing.

Try it online!

Explanation

+/@((!{:)*>:^{:)@i.  Input: integer n
                 i.  Range [0, 1, ..., n-1]
   (           )@    Operate on that range
             {:        Get the last value, n-1
          >:           Increment, range becomes [1, 2, ..., n]
            ^          Exponentiate. [1^(n-1), 2^(n-1), ..., n^(n-1)]
    ( {:)              Get the last value, n-1
     !                 Binomial coefficient. [C(n-1, 0), C(n-1, 1), ..., C(n-1, n-1)]
         *             Multiply
+/@                  Reduce by addition

Answer 8

Maxima, 39 bytes

f(n):=sum(binomial(n,k)*(k+1)^n,k,0,n);

Answer 9

PARI/GP, 35 bytes

n->sum(k=0,n,binomial(n,k)*(k+1)^n)

Answer 10

Axiom, 39 bytes

f(n)==sum(binomial(n,i)*(i+1)^n,i=0..n)

test code and results

(35) -> [[i,f(i)] for i in 0..9]
   (35)
   [[0,1], [1,3], [2,18], [3,170], [4,2200], [5,36232], [6,725200],
    [7,17095248], [8,463936896], [9,14246942336]]

Answer 11

Jelly, 9 bytes

cR×R‘*ƊS‘

Try it online!

How it works

cR×R‘*ƊS‘ - Main link. Argument: n (integer)        e.g.   5
 R        - Range from 1 to n                              [1, 2, 3, 4, 5]
c         - Binomial coefficient                           [5, 10, 10, 5, 1]
      Ɗ   - Last three links as a monad:
   R      -   Link 1: Range from 1 to n                    [1, 2, 3, 4, 5]
    ‘     -   Link 2: Increment                            [2, 3, 4, 5, 6]
     *    -   Link 3: To the power of n                    [32, 243, 1024, 3125, 7776]
  ×       - Multiply, pairwise                             [160, 2430, 10240, 15625, 7776]
       S  - Sum                                            36231
        ‘ - Increment                                      36232