23
3
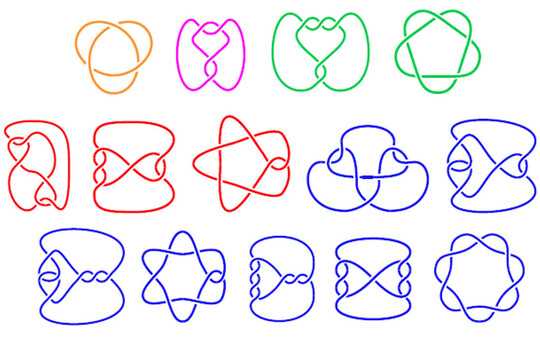
Write a program to draw a 2-D diagram of a knot based on the knot's structure. A knot is exactly what it sounds like: a loop of rope that's tied up. In mathematics, a knot diagram shows where a piece of rope crosses over or under itself to form the knot. Some example knot diagrams are shown below:
There's a break in the line where the rope crosses over itself.
Input: the input describing the knot is an array of integers. A knot where the rope crosses over itself n times can be represented as an array of n integers, each with a value in the range [0, n-1]. Let's call this array K.
To get the array describing a knot, number each of the segments 0 through n-1. Segment 0 should lead to segment 1, which should lead to segment 2, which should lead to segment 3, and so on until segment n-1 loops back and leads to segment 0. A segment ends when another segment of rope crosses over it (represented by a break in the line in the diagram). Let's take the simplest knot - the trefoil knot. After we've numbered the segmnents, segment 0 ends when segment 2 crosses over it; segment 1 ends when segment 0 crosses over it; and segment 2 ends when segment 1 crosses over it. Thus, the array describing the knot is [2, 0, 1]. In general, segment x starts where segment x-1 mod n left off, and ends where segment K[x] crosses over it.
The below image show knot diagrams, with labeled segments and the corresponding arrays that describe the knot.
The top three diagrams are true knots, while the bottom three are loops of rope that cross over themself but aren't actually knotted (but which still have corresponding codes).
Your task is to write a function which takes an array of integers K (you could call it something different) that describes a knot (or loop of rope that's not actually knotted), and which produces the corresponding knot diagram, as described in the above examples. If you can, provide an ungolfed version of your code or an explanation, and also provide sample outputs of your code. The same knot can often be represented in multiple different ways, but if the knot diagram your function outputs satisfies has the input as one of it's possible representations, your solution is valid.
This is code-golf, so shortest code in bytes wins. The line representing the rope can have a thickness of 1 pixel, however under and over-crossings must be clearly distinguishable (the size of the break in the rope should be greater than the thickness of the rope by at least a pixel on either side).
I will upvote answers that rely on built-in knot theory capabilities, but the one that's selected in the end can't rely on built-in knot theory capabilities.
Everything I know about my notation: I believe that there are sequences of values that don't seem to correspond to any knot or unknot. For example, the sequence [2, 3, 4, 0, 1] seems to be impossible to draw.
Aside from that, suppose that you take a crossing and, starting from that crossing, follow the path of the rope in one direction and label every unlabeled crossing that you come across with succesively greater integral values. For alternating knots, there is a simple algorithm to convert my notation into such a labeling, and for alternating knots it's trivial to convert this labeling into a Gauss Code:
template<size_t n> array<int, 2*n> LabelAlternatingKnot(array<int, n> end_at)
{
array<int, n> end_of;
for(int i=0;i<n;++i) end_of[end_at[i]] = i;
array<int, 2*n> p;
for(int& i : p) i = -1;
int unique = 0;
for(int i=0;i<n;i++)
{
if(p[2*i] < 0)
{
p[2*i] = unique;
p[2*end_of[i] + 1] = unique;
++unique;
}
if(p[2*i+1] < 0)
{
p[2*i+1] = unique;
p[2*end_at[i]] = unique;
++unique;
}
}
return p;
}
template<size_t n> auto GetGaussCode(array<int, n> end_at)
{
auto crossings = LabelAlternatingKnot(end_at);
for(int& i : crossings) ++i;
for(int i=1;i<2*n;i+=2) crossings[i] = -crossings[i];
return crossings;
}
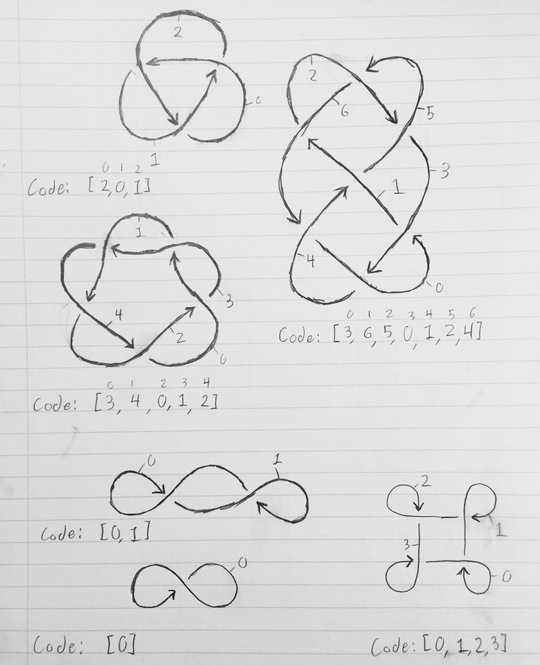
4You should probably ban builtins for doing this. (At this point, I'd be shocked if Mathematica doesn't have one.) – None – 2016-12-07T23:24:05.507
My proposed notation is different from the one mathematica supports, but I added a no-built-ins condition – J. Antonio Perez – 2016-12-07T23:26:39.187
7@ais523 Now I can't use
KnotDatain Mathematica... :'( – JungHwan Min – 2016-12-08T03:16:10.787I'll upvote your answer if you figure out how to implement my notation with KnotData! – J. Antonio Perez – 2016-12-08T03:17:10.347
1I'm curious about the notation you use for the knot crossing diagram. Does it have a name? Is it possible for two non-equivalent knots to have the same array? – xnor – 2016-12-09T23:31:26.670
I am unsure on either of those counts. I came up with the notation because it seemed simple enough to explain, and because I liked how elegant it was. I don't believe it's possible for non-equivalent knots to have the same array, but I haven't proven it yet. I do know that there are multiple arrays which all represent the same knot. – J. Antonio Perez – 2016-12-10T00:26:47.720
@JHM I don't think KnotData will be useful here. In order to use KnotData you would need to 1) determine the knot from the K-notation, then 2) produce a diagram of that knot that has that K-notation. The former will not be unique since a knot can have more than one K-notation depending on the diagram, different knots can have the same K-notation (e.g. trefoil and its mirror), and even a single diagram can have more than one K-notation depending on where you start the numbering and which direction you travel. As for the latter, nothing in KnotData allows you to create arbitrary knot diagrams. – ngenisis – 2016-12-10T04:08:35.790
@ngenisis Yep. You're correct. – JungHwan Min – 2016-12-10T05:09:04.687
2@ais523: Mathematica totally has a
Knotbuiltin! Example usage:<< Units\; Convert[Knot, Mile/Hour]yields1.1507794480235425 Mile/Hour`. (I think this is funny regardless of whether it's true or false; but it's actually true.) – Greg Martin – 2016-12-10T08:34:42.770@GregMartin Knot is a unit commonly used in maritime navigation.
– JungHwan Min – 2016-12-10T15:32:36.620Right, I know that is true—I meant whether it's true that Mathematica has that functionality implemented. – Greg Martin – 2016-12-10T18:26:39.880
I would try this challenge, but all this numerical describing is very ambiguous. [0] is analagous to a loop that is not crossed,, as well as [0,1]. thus [0,1] is equal to [0]. I don't think any program will give you homologous to the examples you provide. Most notably, for the last 3 test cases. – tuskiomi – 2016-12-12T04:48:21.263
1[0], [0,1], [0,1,2], [1,0] and a variety of other arrays all produce "knots" that are equivalent to the unknot, however outputting a simple loop would be incorrect in any of those cases. The notation [0] very specifically means a loop of rope that intersects itself exactly once, and it is very easy to tell whether a figure drawn to the screen satisfies the input notation or not. – J. Antonio Perez – 2016-12-12T06:22:25.177
@JorgePerez but it does not matter weather or not the loop crosses, as the knots are topologically the same thing. they are the same knot. no difference. A program will not be able to simulate the last three test cases any differently from each other. I would also add that your representation is incomplete. The knots that you give for the arrays that you give are analagous to other knots, and can yield more than one proper output. For now, it seems as if your expected outputs are much more complex, and ambiguous than any program can handle with a 1- output limitation. I'm voting to close. – tuskiomi – 2016-12-12T20:14:06.130
1
This should use a different notation (see: http://www.indiana.edu/~knotinfo/descriptions/dt_notation.html)
– Gábor Fekete – 2016-12-13T17:05:50.723@GáborFekete magnificent! – tuskiomi – 2016-12-15T15:52:11.547
I'm trying to prove your notation wrong but I couldn't yet. There is a funny value which got me thinking: [0, 0, 0] (using your notation) which is basically the unknot with two twists in it. – Gábor Fekete – 2016-12-15T16:48:42.357
1I came up with an algorithm to convert my notation into a gauss code for alternating knots, and added some additional information about it – J. Antonio Perez – 2016-12-15T17:28:37.047
Will inputs be guaranteed to represent alternating knots, or does your notation support non-alternating knots as well? – mbomb007 – 2016-12-19T21:24:33.153
I found a possible problem with your notation. You mapped it onto a Gauss Code, but according to this website, "In general, the Gauss Code for some knot diagram cannot reconstruct an equivalent diagram, but a minor revision of the notation will make the reconstruction possible. The revision is called the Extended Gauss Code." The extension is necessary because otherwise there is no means of knowing what the "handedness" of a crossing is.
– mbomb007 – 2016-12-19T22:17:54.540It shouldn't matter for the purpose of this challenge if direction doesn't matter, though. – mbomb007 – 2016-12-19T22:23:25.853
I decided to solve this challenge, but optimizing for (algorithmic) speed, not for golfing. I may optimize for golfing later. My program can do [2, 0, 1] in .05s, and [3, 4, 0, 1, 2] in 8s. I've put in on github here: knot
– isaacg – 2017-01-11T13:12:32.117