Add the Fibonnaci Sequence to the Lucas Sequence

Question

Background of Lucas Numbers

The French mathematician, Edouard Lucas (1842-1891), who gave the name to the Fibonacci Numbers, found a similar series occurs often when he was investigating Fibonacci number patterns.

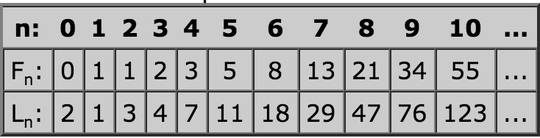
The Fibonacci rule of adding the latest two to get the next is kept, but here we start from 2 and 1 (in this order) instead of 0 and 1 for the (ordinary) Fibonacci numbers. The series, called the Lucas Numbers after him, is defined as follows: where we write its members as Ln, for Lucas:

Challenge

Input

0 < x < ∞
The input will be a positive integer starting at 0.

Output

The output must be a positive integer.

What to do?

Add the Fibonacci numbers to the Lucas numbers.
You will input the index.
The output will be the addition of the Lucas and Fibonacci numbers.

Fibonnaci formula:

F(0) = 0,
F(1) = 1,
F(n) = F(n-1) + F(n-2)

Lucas formula:

L(0) = 2,
L(1) = 1,
L(n) = L(n-1) + L(n-2)

Who wins?

Standard Code-Golf rules apply, so the shortest answer in bytes wins.

Test-cases

A(0) = 2
A(1) = 2
A(5) = 16
A(10) = 178
A(19) = 13,530
A(25) = 242,786

Answer 1

C, 33 bytes

A(n){return n<2?2:A(n-1)+A(n-2);}