Underload, 196 bytes
()()(<svg width="99" height="147">)S(<g transform="translate):S((33,33)">)S((3,0)rotate)*a(*a(~*)*~("><path d="M0h3" stroke="#"/>)~*a(*)**:(-90)a~^~(90)a~^)*::*:**:*^S(</g>)(:*)::*:**:*^S(</svg>)S
I thought it might be interesting to try this challenge in a low-powered esolang; Underload does fairly well for a language with such a low number of commands.
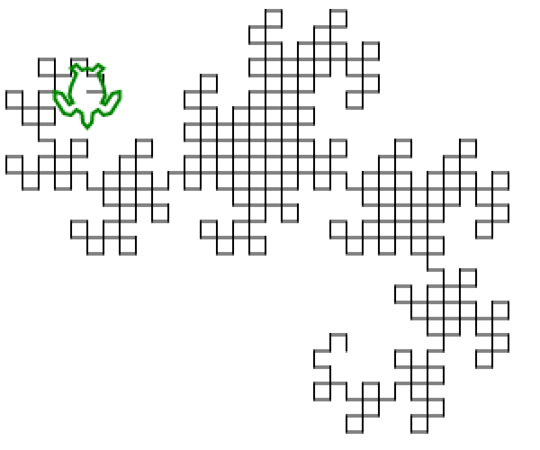
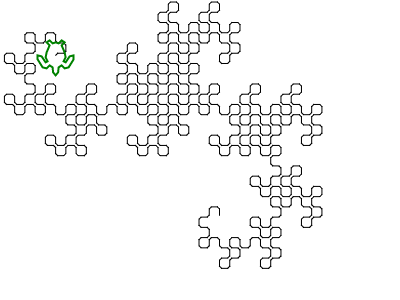
The output is an SVG file with very heavily nested tags, and some golfing shortcuts. So far, I haven't found a browser that can display it (Firefox hangs for several minutes trying to load it, and both Firefox and Chromium give a blank screen). Most image processing programs can't load it either (making it hard to convert to another format), but I managed to load it in the image viewer Eye of Gnome (which is part of the default install on Ubuntu). So I took a screenshot of the image so that you can see it (the actual image has a transparent background, but you can't really screenshot transparent):

We need to specify the image size explicitly. Picking an appropriate orientation for the image, drawing everything at the minimum legal size, and doing the minimum number of iterations specified by the challenge, gives us an image that just fits into 99 pixels wide, saving a byte. It's nice when things work out like that.
The general algorithm used for drawing the image is to maintain two variables (Underload doesn't name variables, but I thought of them as x and y), both initially empty. Then we repeatedly replace (x, y) with (x, turn left and move forward, y) and (x, turn right and move forward, y). After ten iterations, both x and y hold a nine-iteration dragon curve.
There are a few micro-optimizations and Underload-specific tricks, too. In order to avoid too much messing around with the top of the stack, each loop iteration, we start by combining x and y into the function "return the string created by concatenating: x, a turn instruction, the function argument, a move-forward instruction, and y." This function only takes up one space on the stack, so we can duplicate it, call it with -90 as an argument, swap the return value under the duplicate, and call it with 90 as an argument, to get hold of new values for x and y without ever needing to touch more than the top two elements of the stack (which are by far the most commonly accessible). This function is code-generated at runtime. The generator itself is also code-generated at runtime, in order to allow it to reuse the string <g transform="translate that's also used to set the origin of the image. We generate all the open tags first, and then because all the close tags are just </g>, we can output 1024 close tags via simply repeating the string, without worrying about matching them to the open tags. (Writing numbers efficiently in Underload is an interesting problem in its own right; (:*)::*:**:* is probably the most efficient way to write 1024, though, translating to "2 to the power of (1 + 2×2) × 2".
Underload doesn't have any graphics libraries, so I produce SVG using a combination of drawing lines in a fixed position, and rotating the image around a given point; instead of turning the pen, we turn the paper. The idea is that by drawing a line, rotating the entire image, drawing another line, rotating the image again, etc., we can effectively simulate turtle graphics without having to do any arithmetic or use any graphics libraries, as all the lines are drawn in the same location. Of course, that means that we have some very heavily nested rotate-the-image tags, which confuses many SVG viewers.
Styling the image would count against the byte count, so I needed to give the minimum styling needed to display the image. This turns out to be stroke="#", which more or less translates as "the line needs to be some color"; this seems to be expanded to drawing it in black. (Normally you'd specify the color as, say, "#000".) The background is transparent by default. We don't specify a stroke width, but the choice picked by Eye of Gnome leaves everything visible.
Many Underload interpreters struggle with this program, e.g. the one on Try It Online crashes, because it generates some very large strings internally. The original online Underload interpreter works, though. (Interestingly, the very first interpreter was online, so the language was usable online before it was usable offline.)
Something I'm slightly uneasy about is that there only seem to be 1023 line segments here, and we'd expect 1024. It could be that one of the segments at the end isn't being drawn with this algorithm (it'd be drawn on the next iteration instead). If that's disqualifying, it may be possible to adapt the program, but it might well end up considerably longer. (It's not like this challenge is going to win the competition anyway; there are already several shorter entries.)


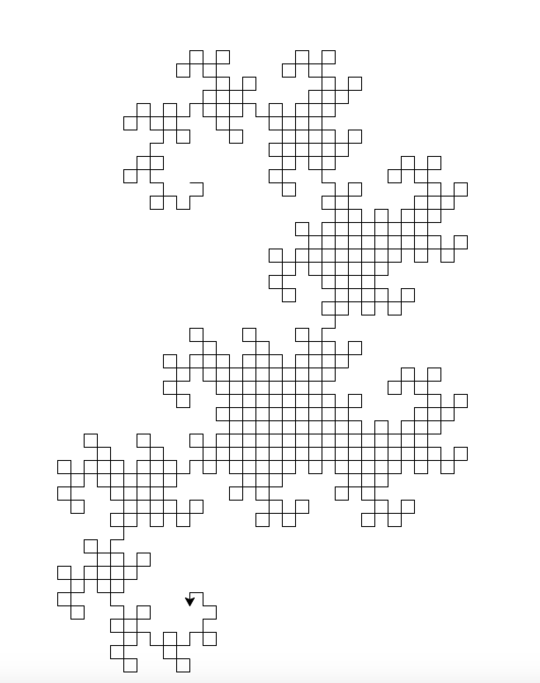
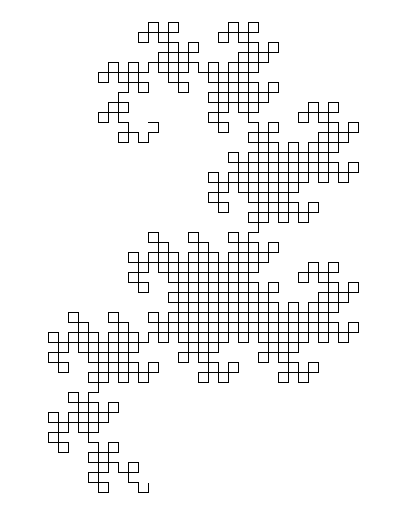







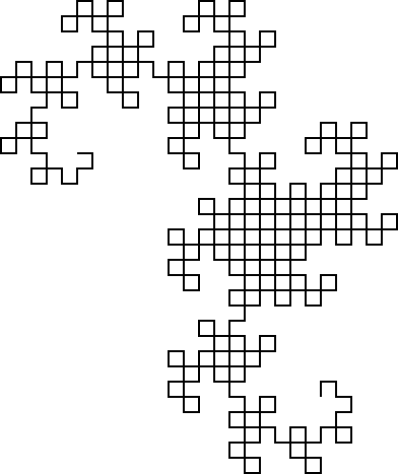
3Are there any specifications about sizing, coloring, etc? As it is the exact output is a bit unclear. – Rɪᴋᴇʀ – 2016-11-20T18:29:00.197
3Related. – Fatalize – 2016-11-20T18:29:09.337
And you don't actually explain what a dragon curve is either, you just show some examples. – Rɪᴋᴇʀ – 2016-11-20T18:29:20.463
6I removed the [tag:dragon-curve] tag because it didn't seem to add anything – Blue – 2016-11-20T18:29:49.870
1Also related. – Martin Ender – 2016-11-20T18:39:46.070
1Added specifications about sizing, colouring, etc – J. Antonio Perez – 2016-11-20T18:44:18.670
@MartinEnder Can you explain how the thue-morse sequence is related to the dragon curve? It´s not immediately apparent. The wikipedia page mentions fractals but only talks about koch curves. – Level River St – 2016-11-20T19:27:49.850
@Oliver That was already flagged up by Fatalize (who by the way asked the previous question.) I think ASCII art is actually slightly more challenging than graphics in this case, so it could indeed be a duplicate, but I`m abstaining from voting. – Level River St – 2016-11-20T19:33:59.397
@LevelRiverSt The constructions of the two sequences (representing left and right turns as 0s and 1s) are almost identical up to reversing part of the sequence when extending it. I've also found a claim online that they're closely related, but their sources were behind a paywall. – Martin Ender – 2016-11-20T19:43:03.403
Because it's specifying that the output must be graphical and not ascii-art, I believe that it's valid and different from the one asking for ascii-art as output. – J. Antonio Perez – 2016-11-20T20:36:32.353
1I'm concerned about a potential loophole in not counting library imports in the byte count. In at least Perl, you can give libraries arbitrary arguments when importing them, and there's probably some library that won't error out on arguments it doesn't understand and some way to figure out what those arguments were after the fact, meaning that the program could be encoded using import statements rather than written the "normal" way. – None – 2016-11-20T23:43:23.947
I would LOVE to see someone abuse the rules in such a convoluted way – J. Antonio Perez – 2016-11-20T23:55:50.500
@Jorge Perez - I loved the video (watched it a couple months back) and have coded a few dragon curves (HTML/Python). I've however not tried to golf it yet and think this is a great idea :) – Teal pelican – 2016-11-21T08:58:27.130
Thanks you so much! I wanted a graphical version because I knew it could be shorter than the ascii version, and also because I liked the output better. I actually have an answer that's 97 bytes, but I'm saving it for a while until I see other people's answers – J. Antonio Perez – 2016-11-21T10:11:22.220
Can the scale of the two axes be different? So the squares are seen as rectangles – Luis Mendo – 2016-11-22T00:33:00.550
I'd accept that, although I'd find the square version to be much more aesthetically pleasing. – J. Antonio Perez – 2016-11-22T00:43:04.117
3This is not a duplicate; the programming techniques to solve it are quite different (except in maybe Charcoal). Most of the answers use turtle graphics libraries, which wouldn't work in an ASCII context at all. – None – 2016-11-22T04:15:46.117
@ais523 not a duplicate, but the techniques are very similar. I used the same turtle graphic concepts here and in my ascii art version. It's still keeping track of x,y position of a moving pen with the right and left turns where needed. – edc65 – 2016-11-22T09:08:27.363
Are built-ins/libraries permitted? – Billywob – 2016-11-22T11:00:41.897