12
3
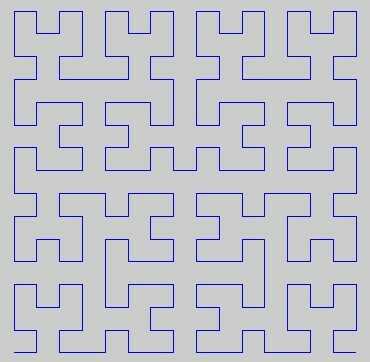
A Hilbert Curve is a type of space-filling curve, and it basically maps a line to a plane. Each point in the line corresponds to just one point in the plane, and each point in the plane corresponds to just one point on the line. Shown are iterations 0 through 4 of the Hilbert Curve:
Iterations 0 up to 4:





The objective of this task: Write code that draws the fourth iteration of the Hilbert Curve, as defined above. Your code should be complete - in other words, if you create a function to draw the Hilbert Curve, your code must call that function. The output can either be displayed directly on the screen, or you can write the output to an image file. The curve may be rotated or flipped, but lines must intersect at right angles and the output cannot be stretched. ASCII art is appreciated but will not be accepted. Shortest code in bytes wins!
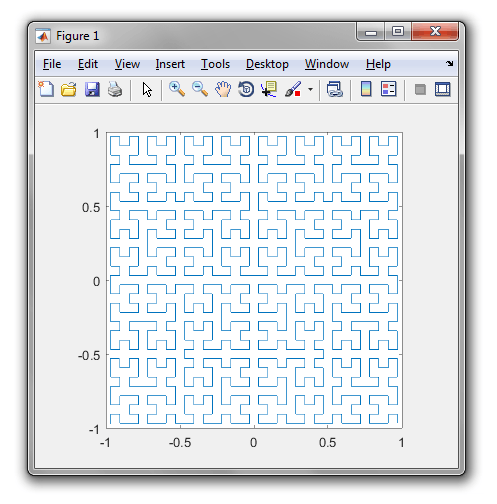
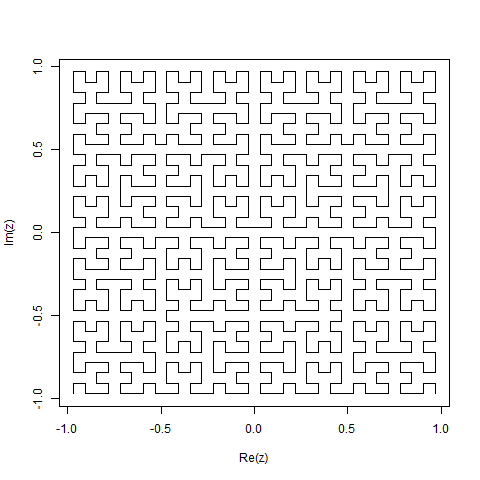
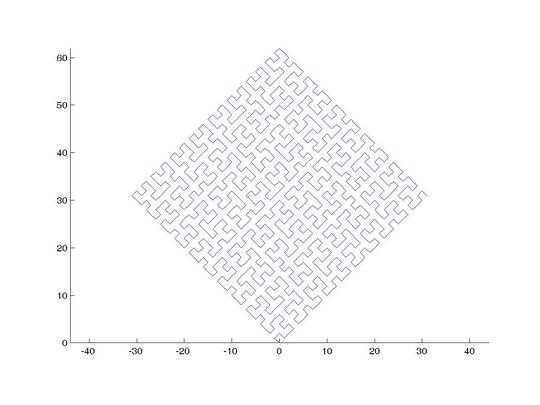
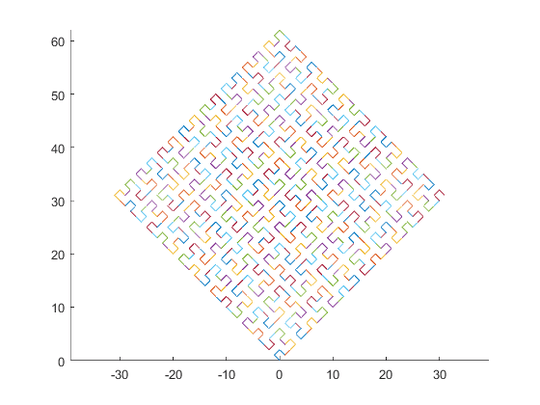


Is the number of times an input? Or can we choose any value at least 4? – Luis Mendo – 2016-11-18T17:28:11.623
Is ASCII art considered graphical? – Gabriel Benamy – 2016-11-18T17:39:30.083
No; sorry - then it'd be a duplicate of another question – J. Antonio Perez – 2016-11-18T17:40:14.110
@JorgePerez Can the curve have a different orientation? Like a vertically flipped or 90-deg rotate version of your examples – Luis Mendo – 2016-11-18T17:41:54.050
Yes! Although the overall shape must still be square – J. Antonio Perez – 2016-11-18T17:42:33.143