44
3
Robbers section
The cops section can be found here.
Challenge
Your task is to outgolf the submissions of the cops in the same language and the same version (for example, Python 3.5 ≠ Python 3.4, so that is not allowed). A submission is outgolfed when the length in bytes is shorter than the original submission. You only need to golf off at least 1 byte in order to crack a submission. E.g. if the task was to perform 2 × n, and the submission was the following:
print(2*input())
You could outgolf the cop by doing the following:
print 2*input()
Or even this (since lambda's are allowed):
lambda x:2*x
Post this with the following header:
##{language name}, <s>{prev byte count}</s> {byte count}, {cop's submission + link}
For example:
Python 2,
1612 bytes, Adnan (+ link to submission)lambda x:2*xComputes A005843, (offset = 0).
In that case, you have cracked the submission.
Scoring
The person with who cracked the most submissions is the winner.
Rules
- The crack submission must be in the same language as the cop submission.
- The same input should result into the same output (so a(2) = 4 should remain 4).
- For languages such as Python, you can import libraries that are standard included within the language. (So, no numpy/sympy etc.)
- Input and output are both in decimal (base 10).
Note
This challenge is finished. The winner of the Robbers section is feersum. The final scores for the CnR are shown below:
- feersum: 16 cracks
- Dennis: 12 cracks
- Leaky Nun: 6 cracks
- Lynn: 4 cracks
- miles: 3 cracks
- Martin Ender: 2 cracks
- Emigna: 2 cracks
- jimmy23013: 1 crack
- Sp3000: 1 crack
- randomra: 1 crack
- alephalpha: 1 crack
- nimi: 1 crack
- Destructible Watermelon: 1 crack
- Dom Hastings: 1 crack
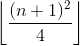
Alternatively,
(**)&2. I tried2&(**)and failed. :( – Dennis – 2016-08-07T04:19:56.700@Dennis
(**)&2works just fine for me :/ but this also works. – Downgoat – 2016-08-07T05:12:10.977