ÆlÐĿĊḊi1
Try it online! or verify all test cases.
Background
We start by successively taking natural logarithms of the input and the subsequent results until the result no longer changes. This works because the extension of the natural logarithm to the complex plane has a fixed point; if z = e-W(-1) ≈ 0.318 + 1.337i – where W denotes the Lambert W function – we have log(z) = z.
For input n, after computing [n, log(n), log(log(n)), …, z], we first apply the ceiling function to each of the results. Jelly's implementation (Ċ) actually computes the imaginary part of complex number instead†, but we're not interested in these anyway.
Once the kth application of log yields a value less than or equal to 1, Ċ will return 1 for the first time. The 0-based index of that first 1 is the desired result.
The straightforward implementation (compute 1-based index, decrement) fails because of edge case 0, which does not have a 1 in its list of logarithms. In fact, for input 0, the sequence of logarithms is
[0, None]
This is because Jelly's logarithm (Æl) is overloaded; it first tries math.log (real logarithm), then cmath.log (complex logarithm), and finally "gives up" and returns None. Fortunately, Ċ is similarly overloaded and simply returns it argument if it cannot round up or take an imaginary part.
Likewise, input 1 returns
[1, 0, None]
which may create problems in other approaches that do or do not involve Ċ.
One way to fix this problem is apply Ḋ (dequeue; removes first element) to the array of logarithms. This maps
0ÆlÐĿ -> [0, None] -> [None]
1ÆlÐĿ -> [1, 0, None] -> [0, None]
so neither list has a 1 now. This way, finding the index of the first 1 will return 0 (not found), which is the desired output for inputs 0 and 1.
How it works
ÆlÐĿĊḊi1 Main link. Argument: n (non-negative integer)
ÐĿ Apply the following link until the results are no longer unique.
Æl Natural logarithm.
Return the array of all unique results.
Ċ Round all resulting real numbers up to the nearest integer. This takes
the imaginary part of complex numbers and does nothing for non-numbers.
Ḋ Dequeue; remove the first item (n) of the array of results.
i1 Find the first index of 1 (0 if not found).
† This is one of the only three atoms in Jelly that are overloaded in a non-obvious manner.
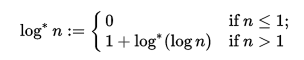
Related. – Oliver Ni – 2016-11-05T23:53:12.867