Regex (ECMAScript), 131 bytes
At least -12 bytes thanks to Deadcode (in chat)
(?=((xx+)(?=\2+$)|x+)+)(?=((x*?)(?=\1*$)(?=(\4xx+?)(\5*(?!(xx+)\7+$)\5)?$)(?=((x*)(?=\5\9*$)x)(\8*)$)x*(?=(?=\5$)\1|\5\10)x)+)\10|x
Try it online!
Output is the length of the match.
ECMAScript regexes make it extremely hard to count anything. Any backref defined outside a loop will be constant during the loop, any backref defined inside a loop will be reset when looping. Thus, the only way to carry state across loop iterations is using the current match position. That’s a single integer, and it can only decrease (well, the position increases, but the length of the tail decreases, and that’s what we can do math to).
Given those restrictions, simply counting coprime numbers seems impossible. Instead, we use Euler’s formula to compute the totient.
Here’s how it looks like in pseudocode:
N = input
Z = largest prime factor of N
P = 0
do:
P = smallest number > P that’s a prime factor of N
N = N - (N / P)
while P != Z
return N
There are two dubious things about this.
First, we don’t save the input, only the current product, so how can we get to the prime factors of the input? The trick is that (N - (N / P)) has the same prime factors > P as N. It may gain new prime factors < P, but we ignore those anyway. Note that this only works because we iterate over the prime factors from smallest to greatest, going the other way would fail.
Second, we have to remember two numbers across loop iterations (P and N, Z doesn’t count since it’s constant), and I just said that was impossible! Thankfully, we can swizzle those two numbers in a single one. Note that, at the start of the loop, N will always be a multiple of Z, while P will always be less than Z. Thus, we can just remember N + P, and extract P with a modulo.
Here’s the slightly more detailed pseudo-code:
N = input
Z = largest prime factor of N
do:
P = N % Z
N = N - P
P = smallest number > P that’s a prime factor of N
N = N - (N / P) + P
while P != Z
return N - Z
And here’s the commented regex:
# \1 = largest prime factor of N
# Computed by repeatedly dividing N by its smallest factor
(?= ( (xx+) (?=\2+$) | x+ )+ )
(?=
# Main loop!
(
# \4 = N % \1, N -= \4
(x*?) (?=\1*$)
# \5 = next prime factor of N
(?= (\4xx+?) (\5* (?!(xx+)\7+$) \5)? $ )
# \8 = N / \5, \9 = \8 - 1, \10 = N - \8
(?= ((x*) (?=\5\9*$) x) (\8*) $ )
x*
(?=
# if \5 = \1, break.
(?=\5$) \1
|
# else, N = (\5 - 1) + (N - B)
\5\10
)
x
)+
) \10
And as a bonus…
Regex (ECMAScript 2018, number of matches), 23 bytes
x(?<!^\1*(?=\1*$)(x+x))
Try it online!
Output is the number of matches. ECMAScript 2018 introduces variable-length look-behind (evaluated right-to-left), which makes it possible to simply count all numbers coprime with the input.
It turns out this is independently the same method used by Leaky Nun's Retina solution, and the regex is even the same length (and interchangeable). I'm leaving it here because it may be of interest that this method works in ECMAScript 2018 (and not just .NET).
# Implicitly iterate from the input to 0
x # Don’t match 0
(?<! ) # Match iff there is no...
(x+x) # integer >= 2...
(?=\1*$) # that divides the current number...
^\1* # and also divides the input
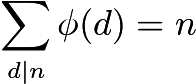
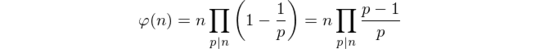
4
Well there was this the other day. I don't think the repeated application makes a sufficient difference, but if anything I'd close the other one, because I also don't think the repeated application adds anything. That said, the bigger difference is that that one allowed built-ins and this one doesn't.
– Martin Ender – 2016-06-22T07:14:48.470Disallowing built-ins apparently has no impact on the answers. – Julie Pelletier – 2016-06-22T07:39:07.527
2@JuliePelletier Why is that? My Mathematica answer would otherwise have been 19 bytes shorter:
EulerPhi– Martin Ender – 2016-06-22T07:40:45.387@JuliePelletier GCD is allowed because calculating GCD is not the intended problem to be solved. Sure, it might bump up the byte counts on these answers, but it doesn't make the challenge better. I'll edit to clarify. – jqblz – 2016-06-22T07:44:13.853