Julia, 66 62 60 bytes
!n=sum(isprime,[a<1<b%3?b:a^2-a*b+b^2for a=[0;0;0:n],b=0:n])
Try it online!
Explanation
We’re interested in the primes in this parallelogram on the complex plane (example for n = 4):
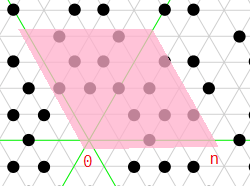
We can split them into primes on the green lines, and on the gray lines.
Wikipedia tells me an Eisenstein number z is a green line Eisenstein prime iff |z| is a natural prime equal to 2 mod 3.
It also says z is a gray line Eisenstein prime iff |z|² = a² − ab + b² is a natural prime.
So we loop over a = 0…n and b = 0…n, and check:
If (a = 0 or b = 0 or a = b) and max(a, b) % 3 = 2, then count whether max(a, b) is a prime.
Else, count whether a² − ab + b² is a prime.
However, we can abuse the distribution’s symmetry. Instead of counting each green line once, we can just count one green line thrice! That is, only check a = 0 and increment the counter by three when we find a green line prime. The a=[0;0;0:n] achieves exactly this.
Since we know we’re only considering the green line a = 0, we can replace max(a, b) by b.
The “green line condition” is nicely expressed in Julia using operator chaining: a<1<b%3.
(For the remaining green lines, we will never return a false positive: if a = b or b = 0 then a² − ab + b² = a², which can’t be prime.)
Ideas
Maybe, instead of writing a^2-a*b+b^2, I can conditionally replace the exponent at b by 1 when a<1<b%3 – then the expression reduces to b. This doesn’t seem to be shorter, but it’s neat!

2Could you provide some test cases? – Alex A. – 2016-06-13T00:35:47.867
I don't understand the test cases. The number of
a,bpairs for2is only4so how could5of them be prime? – Maltysen – 2016-06-13T01:07:28.390@Maltysen let me rewrite the definition – Meow Mix – 2016-06-13T01:20:09.560
1@user3502615 i'm talking about the part where you say "are of the form a+bω for which a,b are natural numbers (including zero) less than n" – Maltysen – 2016-06-13T01:29:48.013
@Maltysen There are 5 numbers: 2ω, 2ω+1,2ω+2,ω+2, and 2 – Meow Mix – 2016-06-13T04:05:49.970
The title is somewhat misleading: the obvious interpretation would be OEIS A003627.
– Peter Taylor – 2016-06-13T15:13:32.817@user3502615 you had less than, not equal to before. it makes sense now – Maltysen – 2016-06-13T17:47:15.187