34
1
The happy ending problem (actually a theorem) states that
Any set of five points in the plane in general position has a subset of four points that form the vertices of a convex quadrilateral.
The problem was so named by Paul Erdős when two mathematicians who first worked on the problem, Ester Klein and George Szekeres, became engaged and subsequently married.
Clarifications:
- General position here means that no three points are collinear.
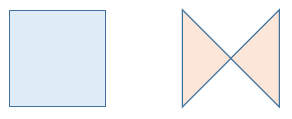
The quadrilateral formed by the four vertices will always be considered to be non-intersecting, irrespective of the order of the points. For example, given the four points
[1 1],[1 2],[2 1],[2 2]the intended quadrilateral is the square, not the bow-tie:A non-intersecting quadrilateral is convex if no interior angle exceeds 180 degrees; or equivalently if both diagonals lie inside the quadrilateral.
The challenge
Given 5 points with positive integer coordinates, output 4 of those points that form a convex quadrilateral.
Rules
If there are several solutions (that is, several sets of 4 points), you can consistently choose to output one of them or all.
Input and output formats are flexible as usual (arrays, lists, list of lists, strings with reasonable separators, etc).
Code golf, fewest bytes wins.
Test cases
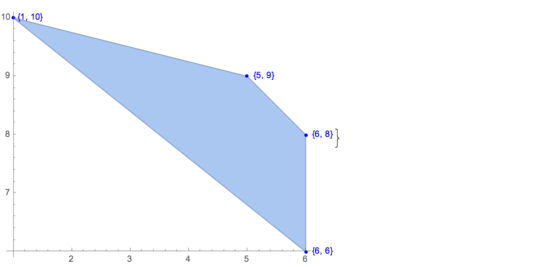
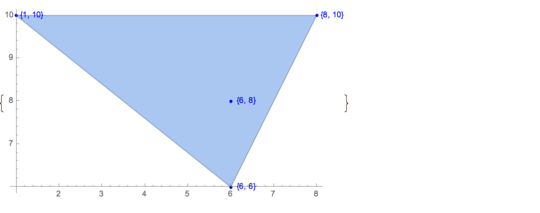
Input:
[6 8] [1 10] [6 6] [5 9] [8 10]There is only one possible output:
[6 8] [1 10] [6 6] [5 9]Input:
[3 8] [7 5] [6 9] [7 8] [5 1]There are five solutions:
[3 8] [7 5] [6 9] [7 8] [3 8] [7 5] [6 9] [5 1] [3 8] [7 5] [7 8] [5 1] [3 8] [6 9] [7 8] [5 1] [7 5] [6 9] [7 8] [5 1]Input:
[4 8] [1 9] [9 9] [10 2] [1 6]There are three solutions:
[4 8] [1 9] [10 2] [1 6] [4 8] [9 9] [10 2] [1 6] [1 9] [9 9] [10 2] [1 6]To illustrate, here are the three solutions to this case:
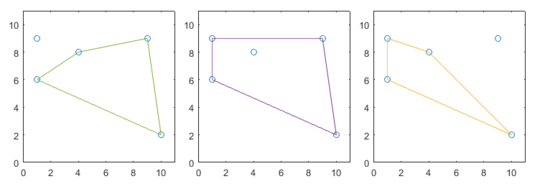
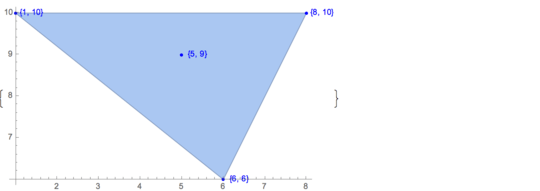
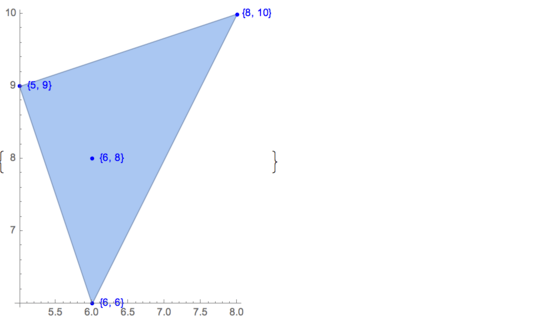
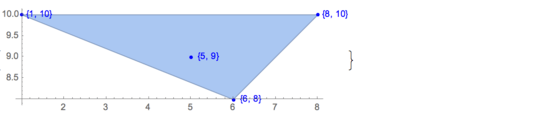

14I'm expecting an answer from Martin with a positive emotion expressed therein. – El'endia Starman – 2016-06-07T19:44:04.827
1
The happy ending problem is not to be confused with the happy Ender problem, which is to find a way to prevent military recruits from discovering the simulations they're playing are real.
– user253751 – 2016-06-09T08:30:18.267