20
1
This question is probably harder than all of those "generate a sequence of numbers" tasks, because this requires TWO sequences working in unison.
Really looking forward to the answers!
In his book "Gödel, Escher, Bach: An Eternal Golden Braid", Douglas Hofstadter has a quite few sequences of numbers inside, all of them rely on the previous term in some way. For information on all of the sequences, see this Wikipedia page.
One pair of sequences that's really interesting is the Female and Male sequences, which are defined like so:
for n > 0.
Here's the Female sequence and the Male sequence.
Your task is, when given an integer n as input, return a list of the Female sequence and the Male sequence, with the amount of terms equal to n, in two lines of output, with the Female sequence on the first line and the Male sequence on the second.
Sample inputs and outputs:
Input: 5
Output: [1, 1, 2, 2, 3] [0, 0, 1, 2, 2]
Input: 10
Output: [1, 1, 2, 2, 3, 3, 4, 5, 5, 6] [0, 0, 1, 2, 2, 3, 4, 4, 5, 6]
NOTE: The separation between lists signifies a line break.
This is code-golf, so shortest code in bytes wins. Also, put an explanation in as well for your code.
Leaderboard
var QUESTION_ID=80608,OVERRIDE_USER=49561;function answersUrl(e){return"https://api.stackexchange.com/2.2/questions/"+QUESTION_ID+"/answers?page="+e+"&pagesize=100&order=desc&sort=creation&site=codegolf&filter="+ANSWER_FILTER}function commentUrl(e,s){return"https://api.stackexchange.com/2.2/answers/"+s.join(";")+"/comments?page="+e+"&pagesize=100&order=desc&sort=creation&site=codegolf&filter="+COMMENT_FILTER}function getAnswers(){jQuery.ajax({url:answersUrl(answer_page++),method:"get",dataType:"jsonp",crossDomain:!0,success:function(e){answers.push.apply(answers,e.items),answers_hash=[],answer_ids=[],e.items.forEach(function(e){e.comments=[];var s=+e.share_link.match(/\d+/);answer_ids.push(s),answers_hash[s]=e}),e.has_more||(more_answers=!1),comment_page=1,getComments()}})}function getComments(){jQuery.ajax({url:commentUrl(comment_page++,answer_ids),method:"get",dataType:"jsonp",crossDomain:!0,success:function(e){e.items.forEach(function(e){e.owner.user_id===OVERRIDE_USER&&answers_hash[e.post_id].comments.push(e)}),e.has_more?getComments():more_answers?getAnswers():process()}})}function getAuthorName(e){return e.owner.display_name}function process(){var e=[];answers.forEach(function(s){var r=s.body;s.comments.forEach(function(e){OVERRIDE_REG.test(e.body)&&(r="<h1>"+e.body.replace(OVERRIDE_REG,"")+"</h1>")});var a=r.match(SCORE_REG);a&&e.push({user:getAuthorName(s),size:+a[2],language:a[1],link:s.share_link})}),e.sort(function(e,s){var r=e.size,a=s.size;return r-a});var s={},r=1,a=null,n=1;e.forEach(function(e){e.size!=a&&(n=r),a=e.size,++r;var t=jQuery("#answer-template").html();t=t.replace("{{PLACE}}",n+".").replace("{{NAME}}",e.user).replace("{{LANGUAGE}}",e.language).replace("{{SIZE}}",e.size).replace("{{LINK}}",e.link),t=jQuery(t),jQuery("#answers").append(t);var o=e.language;/<a/.test(o)&&(o=jQuery(o).text()),s[o]=s[o]||{lang:e.language,user:e.user,size:e.size,link:e.link}});var t=[];for(var o in s)s.hasOwnProperty(o)&&t.push(s[o]);t.sort(function(e,s){return e.lang>s.lang?1:e.lang<s.lang?-1:0});for(var c=0;c<t.length;++c){var i=jQuery("#language-template").html(),o=t[c];i=i.replace("{{LANGUAGE}}",o.lang).replace("{{NAME}}",o.user).replace("{{SIZE}}",o.size).replace("{{LINK}}",o.link),i=jQuery(i),jQuery("#languages").append(i)}}var ANSWER_FILTER="!t)IWYnsLAZle2tQ3KqrVveCRJfxcRLe",COMMENT_FILTER="!)Q2B_A2kjfAiU78X(md6BoYk",answers=[],answers_hash,answer_ids,answer_page=1,more_answers=!0,comment_page;getAnswers();var SCORE_REG=/<h\d>\s*([^\n,]*[^\s,]),.*?(\d+)(?=[^\n\d<>]*(?:<(?:s>[^\n<>]*<\/s>|[^\n<>]+>)[^\n\d<>]*)*<\/h\d>)/,OVERRIDE_REG=/^Override\s*header:\s*/i;body{text-align:left!important}#answer-list,#language-list{padding:10px;width:290px;float:left}table thead{font-weight:700}table td{padding:5px}<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script> <link rel="stylesheet" type="text/css" href="//cdn.sstatic.net/codegolf/all.css?v=83c949450c8b"> <div id="answer-list"> <h2>Leaderboard</h2> <table class="answer-list"> <thead> <tr><td></td><td>Author</td><td>Language</td><td>Size</td></tr></thead> <tbody id="answers"> </tbody> </table> </div><div id="language-list"> <h2>Winners by Language</h2> <table class="language-list"> <thead> <tr><td>Language</td><td>User</td><td>Score</td></tr></thead> <tbody id="languages"> </tbody> </table> </div><table style="display: none"> <tbody id="answer-template"> <tr><td>{{PLACE}}</td><td>{{NAME}}</td><td>{{LANGUAGE}}</td><td>{{SIZE}}</td><td><a href="{{LINK}}">Link</a></td></tr></tbody> </table> <table style="display: none"> <tbody id="language-template"> <tr><td>{{LANGUAGE}}</td><td>{{NAME}}</td><td>{{SIZE}}</td><td><a href="{{LINK}}">Link</a></td></tr></tbody> </table>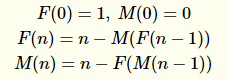
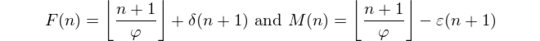
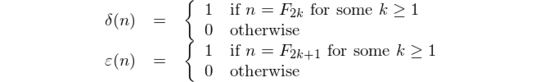

5Can we return a pair of lists from a function, instead of printing the lists? – Zgarb – 2016-05-25T09:54:35.923
Other challenges involving Hofstadter's sequences: Q sequence, figure-figure sequence
– Martin Ender – 2016-05-25T11:17:24.943@Zgarb You can, as long as the two lists are in different lines. – clismique – 2016-05-26T11:55:55.327
2
@DerpfacePython There are no lines in a pair of lists; if a function returns a pair of lists, you can print them however you want. That being said, I'm not a huge fan of the lines requirement, even when printing the output. Cumbersome I/O formats are one of the things to avoid when writing challenges.
– Dennis – 2016-05-26T16:57:25.020@Dennis But it's just a newline in the output - how hard can it really be? At most, it's around 5 bytes of code. – clismique – 2016-05-27T09:58:38.657
4It's no big deal for some approaches/languages, but it can make a big difference for others. In C, a lot of bytes could be saved by printing the sequences in columns rather than rows. In Python, the shortest approach I can think of is a recursive lambda similar to my recursive Julia answer that returns a pair of lists, but having to convert that into a string with a linefeed makes it a lot longer, even longer than the full program posted by Sp3000. Other approaches, such as a recursive solution that counts down instead of up, are completely ruled out since it is impossible to add the newline. – Dennis – 2016-05-27T15:38:47.543