Unfolding the Hexagony source code

Question

Introduction

If you're not familiar with Hexagony, it's an esoteric language created by Martin Büttner. The thing is that this language accepts multiple forms for the program. The following programs are all equivalent:

abcdefg

and

 a b
c d e
 f g

So basically, the code has been rolled up into a regular hexagon. But note that adding a new command to the code, which would be abcdefgh would result into the following program:

  a b c
 d e f g
h . . . .
 . . . .
  . . .

As you can see, the first step is rolling up the code into a hexagon, and after that the hexagon is filled in with no-ops (.) to the next centered hexagonal number.

Your task is simple, when given a string (the source code), output the full hexagon source code.

The rules

• You may provide a program or a function.
• Leading whitespace is allowed, but only when the hexagon doesn't get out of shape
• Trailing whitespace is allowed.
• Note that whitespace in the program are ignored. So a b c is equal to abc
• Only the printable ASCII characters (32 - 126) are used, so only the regular Space character is ignored.
• Assume that the length of the string is greater than 0.
• This is code-golf, so the submission with the least amount of bytes wins!

Test cases

Input: ?({{&2'2':{):!/)'*/

Output:
  ? ( {
 { & 2 '
2 ' : { )
 : ! / )
  ' * /


Input: H;e;l;d;*;r;o;Wl;;o;*433;@.>;23<\4;*/

Output:
   H ; e ;
  l ; d ; *
 ; r ; o ; W
l ; ; o ; * 4
 3 3 ; @ . >
  ; 2 3 < \
   4 ; * /


Input: .?'.) .@@/'/ .!.>   +=(<.!)}    (  $>( <%

Output:
   . ? ' .
  ) . @ @ /
 ' / . ! . >
+ = ( < . ! )
 } ( $ > ( <
  % . . . .
   . . . .

Answer 1

Pyth, 57 54 50 49 48 46

V+UJfgh*6sUTlK-zd1_UtJ+*d-JNjd:.[K\.^TJZ=+Z+JN

Test Suite

Prints a leading space on each line.

This version requires a proof that 10^n >= 3n(n - 1) + 1 for all n >= 1. Thanks to ANerdI and ErickWong for providing proofs.

Following these inequalities: 10^n > (1+3)^n = 1 + 3n + 9n(n - 1) + ... > 3n(n - 1) + 1 one can easily see that this is correct for n >= 2. Examining the n = 1 case is rather trivial, giving 10 > 1.

Alternatively, taking the derivatives of these equations twice shows that 10^n has a greater second derivative for all n >= 1, which can then be cascaded down to the first derivatives, and finally to the original equations.

Explanation

              ##  Implicit: z=input(); Z=0
Jf...1        ##  Save to J the side length of the hexagon the code fills up
              ##  by finding the first number such that:
gh*6sUT       ##  the the T'th hexagonal number is greater than...
              ##  Computes 6 * T'th triangular number (by using sum 1..T-1) + 1
    lK-zd     ##  ...the length of the code without spaces (also save the string value to K)
V+UJ_UtJ      ##  For loop over N = [0, 1, ..., J-1, ..., 0]:
+*d-JN        ##  append J - N spaces to the front of the line
jd            ##  riffle the result of the next operation with spaces
:.[K\.yJ      ##  slice the string given by K padded to be the length of the Jth hexagon
              ##  number with noops
Z=+Z+JN       ##  from Z to Z + J + N, then set Z to be Z + J + N

Answer 2

Hexagony, 271 bytes

I present to you, the first 3% of a Hexagony self-interpreter...

|./...\..._..>}{<$}=<;>'<..../;<_'\{*46\..8._~;/;{{;<..|M..'{.>{{=.<.).|.."~....._.>(=</.\=\'$/}{<}.\../>../..._>../_....@/{$|....>...</..~\.>,<$/'";{}({/>-'(<\=&\><${~-"~<$)<....'.>=&'*){=&')&}\'\'2"'23}}_}&<_3.>.'*)'-<>{=/{\*={(&)'){\$<....={\>}}}\&32'-<=._.)}=)+'_+'&<

Try it online! You can also run it on itself, but it will take about 5-10 seconds.

In principle this might fit into side-length 9 (for a score of 217 or less), because this uses only 201 commands, and the ungolfed version I wrote first (on side-length 30) needed only 178 commands. However, I'm pretty sure it would take forever to actually make everything fit, so I'm not sure whether I'll actually attempt it.

It should also be possible to golf this a bit in size 10 by avoiding the use of the last one or two rows, such that the trailing no-ops can be omitted, but that would require a substantial rewrite, as one of the first path joins makes use of the bottom left corner.

Explanation

Let's start by unfolding the code and annotating the control flow paths:

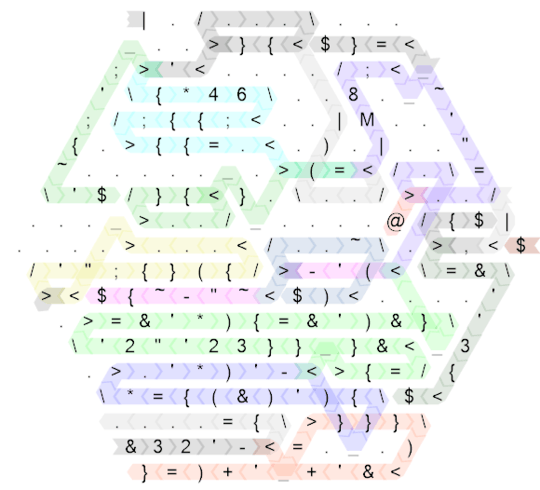
That's still quite messy, so here is the same diagram for the "ungolfed" code which I wrote first (in fact, this is side-length 20 and originally I wrote the code on side-length 30 but that was so sparse that it wouldn't improve the readability at all, so I compacted it just a little bit to make the size a bit more reasonable):

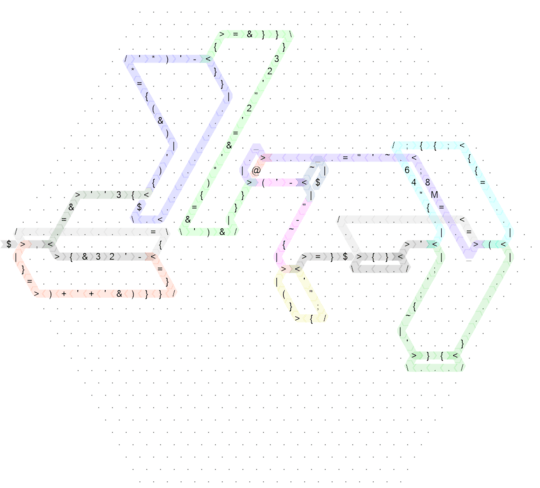
^{Click for larger version.}

The colours are exactly the same apart from a few very minor details, the non-control-flow commands are also exactly the same. So I'll be explaining how this works based on the ungolfed version, and if you really want to know how the golfed one works, you can check which parts there correspond to which in the larger hexagon. (The only catch is that the golfed code starts with a mirror so that the actual code begins in the right corner going left.)

The basic algorithm is almost identical to my CJam answer. There are two differences:

• Instead of solving the centred hexagonal number equation, I just compute consecutive centred hexagonal numbers until one is equal to or larger than the length of the input. This is because Hexagony does not have a simple way to compute a square root.
• Instead of padding the input with no-ops right away, I check later if I've already exhausted the commands in the input and print a . instead if I have.

That means the basic idea boils down to:

• Read and store input string while computing its length.
• Find the smallest side-length N (and corresponding centred hexagonal number hex(N)) which can hold the entire input.
• Compute the diameter 2N-1.
• For each line, compute the indent and the number of cells (which sum to 2N-1). Print the indent, print the cells (using . if the input is already exhausted), print a linefeed.

Note that there are only no-ops so the actual code starts in the left corner (the $, which jumps over the >, so the we really start on the , in the dark grey path).

Here is the initial memory grid:

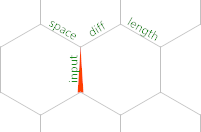
So the memory pointer starts out on edge labelled input, pointing North. , reads a byte from STDIN or a -1 if we've hit EOF into that edge. Hence, the < right after is a conditional for whether we've read all the input. Let's remain in the input loop for now. The next code we execute is

{&32'-

This writes a 32 into the edge labelled space, and then subtracts it from the input value in the edge labelled diff. Note that this can never be negative because we're guaranteed that the input contains only printable ASCII. It will be zero when the input was a space. (As Timwi points out, this would still work if the input could contain linefeeds or tabs, but it would also strip out all other unprintable characters with character codes less than 32.) In that case, the < deflects the instruction pointer (IP) left and the light grey path is taken. That path simply resets the position of the MP with {= and then reads the next character - thus, spaces are skipped. Otherwise, if the character was not a space, we execute

=}}})&'+'+)=}

This first moves around the hexagon through the length edge until its opposite the diff edge, with =}}}. Then it copies the value from opposite the length edge into the length edge, and increments it with )&'+'+). We'll see in a second why this makes sense. Finally, we move the a new edge with =}:

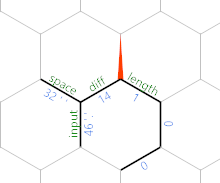
(The particular edge values are from the last test case given in the challenge.) At this point, the loop repeats, but with everything shifted one hexagon northeast. So after reading another character, we get this:

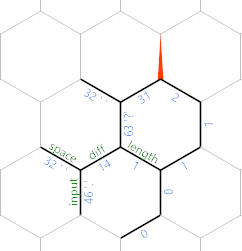
Now you can see that we're gradually writing the input (minus spaces) along the northeast diagonal, with the characters on every other edge, and the length up to that character being stored parallel to the edge labelled length.

When we're done with the input loop, memory will look like this (where I've already labelled a few new edges for the next part):

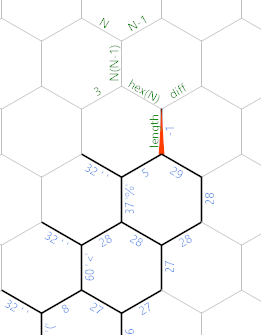
The % is the last character we read, the 29 is the number of non-space characters we read. Now we want to find the side-length of the hexagon. First, there is some linear initialisation code in the dark green/grey path:

=&''3{

Here, =& copies the length (29 in our example) into the edge labelled length. Then ''3 moves to the edge labelled 3 and sets its value to 3 (which we just need as a constant in the computation). Finally { moves to the edge labelled N(N-1).

Now we enter the blue loop. This loop increments N (stored in the cell labelled N) then computes its centered hexagonal number and subtracts it from the input length. The linear code which does that is:

{)')&({=*'*)'-

Here, {) moves to and increments N. ')&( moves to edge labelled N-1, copies N there and decrements it. {=* computes their product in N(N-1). '*) multiplies that by the constant 3 and increments the result in the edge labelled hex(N). As expected, this is the Nth centered hexagonal number. Finally '- computes the difference between that and the input length. If the result is positive, the side-length is not large enough yet, and the loop repeats (where }} move the MP back to the edge labelled N(N-1)).

Once the side-length is large enough, the difference will be zero or negative and we get this:

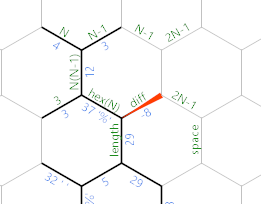
First off, there is now the really long linear green path which does some necessary initialisation for the output loop:

{=&}}}32'"2'=&'*){=&')&}}

The {=& starts by copying the result in the diff edge into the length edge, because we later need something non-positive there. }}}32 writes a 32 into the edge labelled space. '"2 writes a constant 2 into the unlabelled edge above diff. '=& copies N-1 into the second edge with the same label. '*) multiplies it by 2 and increments it so that we get the correct value in the edge labelled 2N-1 at the top. This is the diameter of the hexagon. {=&')& copies the diameter into the other edge labelled 2N-1. Finally }} moves back to the edge labelled 2N-1 at the top.

Let's relabel the edges:

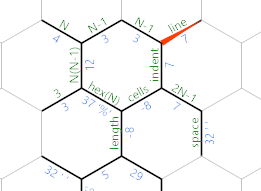
The edge we're currently on (which still holds the diameter of the hexagon) will be used to iterate over the lines of the output. The edge labelled indent will compute how many spaces are needed on the current line. The edge labelled cells will be used to iterate over the number of cells in the current line.

We're now on the pink path which computes indent. ('- decrements the lines iterator and subtracts it from N-1 (into the indent edge). The short blue/grey branch in the code simply computes the modulus of the result (~ negates the value if it's negative or zero, and nothing happens if it's positive). The rest of the pink path is "-~{ which subtracts the indent from the diameter into the cells edge and then moves back to the indent edge.

The dirty yellow path now prints the indentation. The loop contents are really just

'";{}(

Where '" moves to the space edge, ; prints it, {} moves back to indent and ( decrements it.

When we're done with that the (second) dark grey path searches for next character to print. The =} moves in position (which means, onto the cells edge, pointing South). Then we have a very tight loop of {} which simply moves down two edges in the South-West direction, until we hit the end of the stored string:

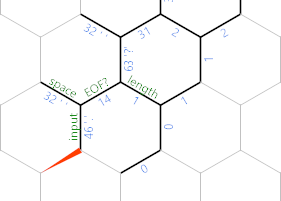
Notice that I've relabelled one edge there EOF?. Once we've processed this character, we'll make that edge negative, so that the {} loop will terminate here instead of the next iteration:

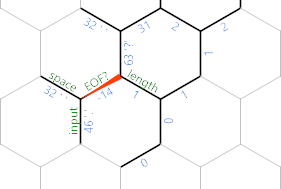
In the code, we're at the end of the dark grey path, where ' moves back one step onto the input character. If the situation is one of the last two diagrams (i.e. there's still a character from the input we haven't printed yet), then we're taking the green path (the bottom one, for people who aren't good with green and blue). That one is fairly simple: ; prints the character itself. ' moves to the corresponding space edge which still holds a 32 from earlier and ; prints that space. Then {~ makes our EOF? negative for the next iteration, ' moves a back a step so that we can return to the North-West end of the string with another tight }{ loop. Which ends on the length cell (the non-positive one below hex(N). Finally } moves back to the cells edge.

If we've already exhausted the input though, then the loop which searches for EOF? will actually terminate here:

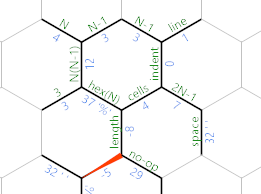
In that case ' moves onto the length cell, and we're taking the light blue (top) path instead, which prints a no-op. The code in this branch is linear:

{*46;{{;{{=

The {*46; writes a 46 into the edge labelled no-op and prints it (i.e. a period). Then {{; moves to the space edge and prints that. The {{= moves back to the cells edge for the next iteration.

At this point the paths join back together and ( decrements the cells edge. If the iterator is not zero yet, we will take the light grey path, which simply reverses the MP's direction with = and then goes looking for the next character to print.

Otherwise, we've reached the end of the current line, and the IP will take the purple path instead. This is what the memory grid looks like at that point:

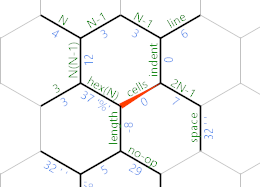
The purple path contains this:

=M8;~'"=

The = reverses the direction of the MP again. M8 sets the sets its value to 778 (because the character code of M is 77 and digits will append themselves to the current value). This happens to be 10 (mod 256), so when we print it with ;, we get a linefeed. Then ~ makes the edge negative again, '" moves back to the lines edge and = reverses the MP once more.

Now if the lines edge is zero, we're done. The IP will take the (very short) red path, where @ terminates the program. Otherwise, we continue on the purple path which loops back into the pink one, to print another line.

---

Control flow diagrams created with Timwi's HexagonyColorer. Memory diagrams created with the visual debugger in his Esoteric IDE.

Answer 3

CJam, 56 52 50 48 bytes

My first thought was, "hey I already have code for this!" But then I couldn't be bothered to pull the necessary pieces together from the Ruby code, especially because they didn't seem very suitable to being golfed. So I tried something else in CJam instead...

lS-{_,4*(3/mq:D1%}{'.+}wD{D(2/-z_S*D@-@/(S*N@s}/

Test it here.

Explanation

A bit of maths about centred hexagonal numbers first. If the regular hexagon has side length N, then it will contain 3N(N-1)+1 cells, which has to equal the source code length k. We can solve that N because it's a simple quadratic equation:

N = 1/2 ± √(1/4 + (k-1)/3)

We can ignore the negative root, because that gives a negative N. For this to have a solution, we need the square root be a half-integer. Or in other words, √(1 + 4(k-1)/3) = √((4k-1)/3) needs to be an integer (luckily, this integer happens to be the diameter D = 2N-1 of the hexagon, which we'll need anyway). So we can repeatedly add a single . until that condition is met.

The rest is a simple loop which lays out the hexagon. A useful observation for this part is that the spaces in the indentation plus the non-spaces in the code in each line add up to the diameter.

lS-     e# Read input and remove spaces.
{       e# While the first block yields something truthy, evaluate the second...
  _,    e#   Duplicate the code and get its length k.
  4*(   e#   Compute 4k-1.
  3/    e#   Divide by 3.
  mq    e#   Take the square root.
  :D    e#   Store this in D, just in case we're done, because when we are, this happens
        e#   to be the diameter of the hexagon.
  1%    e#   Take modulo 1. This is 0 for integers, and non-zero for non-integers.
}{      e# ...
  '.+   e#   Append a no-op to the source code.
}w
D{      e# For every i from 0 to D-1...
  D(2/  e#   Compute (D-1)/2 = N, the side length.
  -z    e#   Subtract that from the current i and get its modulus. That's the size of the
        e#   indentation on this line.
  _S*   e#   Duplicate and get a string with that many spaces.
  D@-   e#   Subtract the other copy from D to get the number of characters of code
        e#   in the current line.
  @/    e#   Pull up the source code and split into chunks of this size.
  (S*   e#   Pull off the first chunk and riffle it with spaces.
  N     e#   Push a linefeed character.
  @s    e#   Pull up the remaining chunks and join them back into a single string.
}/

It turns out that we don't need to use double arithmetic at all (except for the square root). Due to the multiplication by 4, there are no collisions when dividing by 3, and the desired k will be the first to yield an integer square root.

Answer 4

Perl, 203 200 198

includes + 1 for -p

s/\s//g;{($l=y///c)>($h=1+3*++$n*($n-1))&&redo}$s=$_.'.'x($h-$l);for($a=$n;$a<($d=2*$n-1);$a++){$s=~s/.{$a}/$&\n/,$s=reverse($s)for 0..1}$_=join$/,map{(' 'x abs($n-$i++-1)).$_}$s=~/\S+/g;s/\S/ $&/g

run as: echo abc | perl -p file.pl

A very naive approach:

#!/usr/bin/perl -p

s/\s//g;                            # ignore spaces and EOL etc.
{                                   # find the smallest hex number:
    ($l=y///c)                      # calc string length
    > ($h=1+3*++$n*($n-1))          # 
    && redo                         # (should use 'and', but..)
}

$s = $_                             # save $_ as it is used in the nested for
   . '.' x ($h-$l);                 # append dots to fill hexagon

for ( $a = $n; $a < ($d=2*$n-1); $a++ )
{
        $s=~s/.{$a}/$&\n/,          # split lines
        $s=reverse($s)              # mirror
    for 0..1                        # twice
}

$_ = join$/,                        # join using newline
map {                               # iterate the lines
    (' 'x abs($n-$i++-1)) .$_       # prepend padding
} $s=~/\S+/g;                       # match lines

s/\S/ $&/g                          # prepend spaces to characters
                                    # -p takes care of printing $_

---

• update 200 save a byte moving variable assignment, and another 2 by omitting final ;; code itself under 200 bytes now!
• update 198 save 2 bytes by using $s=~/\S+/g instead of split/\n/,$s

Answer 5

JavaScript (ES6), 162 172

Anonymous function

The hexagon size is found resolving the equation from wikipedia

3*n*(n-1)-1 = l

The solving formula is basically

n = ceil(3+sqrt(12*l-3))/6)

With some algebra and some approximation (thx to @user18655 too) it becomes

n = trunc(sqrt(l/3-1/12)+1.4999....)

s=>eval("s=s.match(/\\S/g);m=n=Math.sqrt(s.length/3-1/12)+1.49999|0;p=o=``;for(i=n+n;--i;i>n?++m:--m)for(o+=`\n`+` `.repeat(n+n-m),j=m;j--;o+=` `)o+=s[p++]||`.`")

More readable

s=>{
  s=s.match(/\S/g);
  m=n=Math.sqrt(s.length/3-1/12)+1.49999;
  p=o='';
  for(i=n+n; --i; i>n?++m:--m)
    for(o += '\n'+' '.repeat(n+n-m), j=m; j--; o += ' ')
      o+=s[p++]||'.';
  return o
}

Test snippet (better full page - running time ~ 1 minute)

f=s=>eval("s=s.match(/\\S/g);m=n=Math.sqrt(s.length/3-1/12)+1.49999|0;p=o=``;for(i=n+n;--i;i>n?++m:--m)for(o+=`\n`+` `.repeat(n+n-m),j=m;j--;o+=` `)o+=s[p++]||`.`")

t=0;
r='0';
(T=_=>t++<816?(O.innerHTML=f(r=t%10+r),setTimeout(T,20)):0)()

pre { font-size: 66% }

<pre id=O></pre>

Answer 6

Pyth, 52 51 bytes

Jfgh**3TtTl=H-zd1=+H*\.*lHTV+UJt_UJAcH]+JN+*-JNdjdG

Try it online. Test suite.

Each line has one extra leading space, as permitted by the OP.

Explanation

 f              1          |   find first number n for which
             -zd           |           remove spaces from input
           =H              |         put result in H
          l                |       length of input without spaces
  g                        |     is less than or equal to
   h**3TtT                 |       nth centered hexagonal number
J                          | put result (hexagon side length) in J
                           |
      *lHT                 |      ten times length of input without spaces
   *\.                     |   that amount of dots
=+H                        | append to H
                           |
  UJ                       |    numbers 0 up to side length - 1
 +  t_UJ                   |   add numbers side length - 2 down to 0
V                          | loop over result
            +JN            |       current loop number + side length
         cH]               |     split to two parts at that position
        A                  |   put parts to G and H
                 -JN       |       side length - current loop number - 1
                *   d      |     that many spaces
                     jdG   |     join code on the line (G) by spaces
               +           |   concatenate parts and print

Answer 7

Retina, 161 bytes

Thanks to FryAmTheEggman for saving 2 bytes.

This answer is non-competing. Retina has seen a few updates since this challenge, and I'm pretty sure I'm using some of the newer features (although I haven't checked).

Byte count assumes ISO 8859-1 encoding. The first line contains a single space. Note that most of the · are actually centre dots (0xB7).

 

^
$._$*·¶
^·¶
¶
((^·|\2·)*)·\1{5}·+
$2·
^·*
$.&$* ·$&$&$.&$* 
M!&m`(?<=(?= *(·)+)^.*)(?<-1>.)+(?(1)!)|^.+$
+m`^( *·+)· *¶(?=\1)
$& 
·
 ·
O$`(·)|\S
$1
·
.
G-2`

Try it online!

Well...

Explanation

It seems easiest to build the layout first using just a single character (· in this case) and then fill the resulting layout with the input characters. The main reasons for this are that using a single character lets me make use of backreferences and character repetition, where laying out the input directly would require expensive balancing groups.

Although it doesn't look like much, this first stages removes spaces from the input.

^
$._$*·¶

We start by prepending an additional line which contains M centre dots, where M is the length of the input (after removing spaces).

^·¶
¶

If the input was a single character, we remove that centre dot again. This is an unfortunate special case that isn't covered by the next stage.

((^·|\2·)*)·\1{5}·+
$2·

This computes the required side length N minus 1. Here is how that works: centred hexagonal numbers are of the form 3*N*(N-1) + 1. Since triangular numbers are N*(N-1)/2, that means hexagonal numbers are six times a triangular number plus 1. That's convenient because matching triangular numbers (which are really just 1 + 2 + 3 + ... + N) in a regex is fairly easy with forward references. The (^·|\2·)* matches the largest triangular number it can. As a nice bonus, $2 will then hold the index of this triangular number. To multiply it by 6, we capture it into group 1 and match it another 5 times. We make sure there are at least two more · with the · and the ·+. This way the index of the found triangular number doesn't increase until there's one character more than a centred hexagonal number.

In the end, this match gives us two less than the side-length of the required hexagon in group $2, so we write that back together with one more centre dot to get N-1.

^·*
$.&$* ·$&$&$.&$* 

This turns our string of N-1 centre dots into N-1 spaces, 2N-1 centre dots and another N-1 spaces. Note that this is the maximum indentation, followed by the diameter of the hexagon, followed by the indentation again.

M!&m`(?<=(?= *(·)+)^.*)(?<-1>.)+(?(1)!)|^.+$

This is unpleasantly long, but it basically just gives us all overlapping matches, which are either a) 2N-1 characters long and on the first line or b) the second line. This expands the result from the previous stage into the full, but weirdly indented hexagon. E.g. for input 12345678 we'd get:

  ···
 ····
·····
···· 
···  
12345678

This is why we needed to append spaces in the previous stage as well.

+m`^( *·+)· *¶(?=\1)
$& 

This fixes the indentation of the lines after the centre, by repeatedly indenting any line that is shorter than the previous (ignoring trailing spaces), so we get this:

  ···
 ····
·····
 ···· 
  ···  
12345678

Now we just insert some spaces with

·
 ·

Which gives us:

   · · ·
  · · · ·
 · · · · ·
  · · · · 
   · · ·  
12345678

Phew, that's done.

O$`(·)|\S
$1

Time to fill the input string into the centre dots. This is done with the help of a sort stage. We match all centre dots and each character on the last line, and we sort them by the result of the given substitution. That substitution is empty for the characters on the last line and · for the centre dots, so what happens is that the centre dots are simply sorted to the end (since sorting is stable). This moves the input characters into place:

   1 2 3
  4 5 6 7
 8 · · · ·
  · · · · 
   · · ·  
········

Just two things left now:

·
.

This turns centre dots into regular periods.

G-2`

And this discards the last line.

Answer 8

JavaScript (ES6), 144 bytes

(s,n=1,l=0,p=0,m=s.match(/\S/g))=>m[n]?f(s,n+6*++l,l):[...Array(l+l+1)].map((_,i,a)=>a.map((_,j)=>j<l-i|j<i-l?``:m[p++]||`.`).join` `).join`\n`

Where \n represents the literal newline character. Uses a technique for creating a hexagon that I've previously used on several other hexagonal-grid answers. For ES7 taking square roots works out slightly shorter than the recursive approach:

(s,p=0,m=s.match(/\S/g),l=(~-m.length/3)**.5+.5|0)=>[...Array(l+l+1)].map((_,i,a)=>a.map((_,j)=>j<l-i|j<i-l?``:m[p++]||`.`).join` `).join`\n`

Answer 9

Python 3, 144 bytes

c=input().replace(' ','')
n=x=1
while x<len(c):x+=n*6;n+=1
c=c.ljust(x,'.')
while c:print(' '*(x-n)+' '.join(c[:n]));c=c[n:];n-=(len(c)<x/2)*2-1

Try it online!

This uses a rather varying amount of leading whitespace for different sized hexagons, but the general shape survives.