27
7
Rules are simple:
- First n primes (not primes below n), should be printed to standard output separated by newlines (primes should be generated within the code)
- primes cannot be generated by an inbuilt function or through a library, i.e. use of a inbuilt or library function such as, prime = get_nth_prime(n), is_a_prime(number), or factorlist = list_all_factors(number) won't be very creative.
Scoring - Say, we define Score = f([number of chars in the code]), O(f(n)) being the complexity of your algorithm where n is the number of primes it finds. So for example, if you have a 300 char code with O(n^2) complexity, score is 300^2 = 90000, for 300 chars with O(n*ln(n)), score becomes 300*5.7 = 1711.13 (let's assume all logs to be natural logs for simplicity)
Use any existing programming language, lowest score wins
Edit: Problem has been changed from finding 'first 1000000 primes' to 'first n primes' because of a confusion about what 'n' in O(f(n)) is, n is the number of primes you find (finding primes is the problem here and so complexity of the problem depends on the number of primes found)
Note: to clarify some confusions on complexity, if 'n' is the number of primes you find and 'N' is the nth prime found, complexity in terms of n is and N are not equivalent i.e. O(f(n)) != O(f(N)) as , f(N) != constant * f(n) and N != constant * n, because we know that nth prime function is not linear, I though since we were finding 'n' primes complexity should be easily expressible in terms of 'n'.
As pointed out by Kibbee, you can visit this site to verify your solutions (here, is the old google docs list)
Please Include these in your solution -
what complexity your program has (include basic analysis if not trivial)
character length of code
the final calculated score
This is my first CodeGolf Question so, if there is a mistake or loophole in above rules please do point them out.
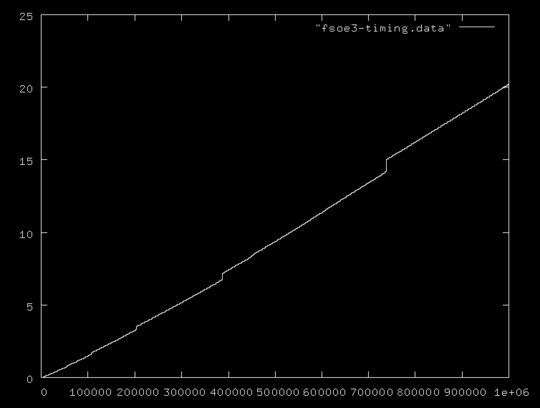
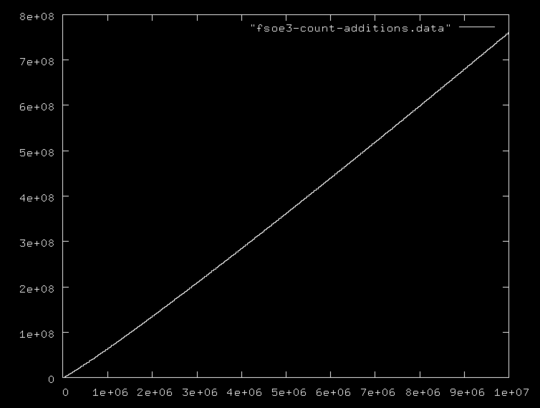
5
This is very similar to http://codegolf.stackexchange.com/questions/5977/list-of-primes-under-a-million .
– Gareth – 2012-06-10T17:12:58.360Nope I think it is very different this says to find first million primes not primes under million, the two problems are very different. – Optimus – 2012-06-10T17:19:02.050
also scoring criterion here accounts for how efficiently you do it. I didn't find any ingrained judgement of efficiency there – Optimus – 2012-06-10T17:22:13.137
2My answer for that one was
1[\p:i.78498my answer for this would be1[\p:i.1000000. Even assuming that J's internal prime algorithm is O(n^2) my score would still only be 196. – Gareth – 2012-06-10T17:23:50.747Is it a direct function in J that gives primes? if that is so, use of such functions as one that gives you a prime or checks if the number is prime is unfair, and I will modify problem statement to incorporate that – Optimus – 2012-06-10T17:35:36.193
1@Optimus: You could do a md5sum of the primes file and print the handful of bytes, instead of uploading 8M. – user unknown – 2012-06-10T17:36:15.450
1I assume with complexity
f(n)you meannthe number of primes to be calculated. In your question the number is fixed, so every solution would beO(1)and thus have the same score, namely1. Also basis of the logarithmlog2(n)in the complexity is not well-specified - but has influence on the proposed scoring. – Howard – 2012-06-10T17:57:22.397@Gareth as I said "prime numbers should be generated within the code" using a direct function really makes it a moot point to ask this in the first place – Optimus – 2012-06-10T17:58:01.627
@Howard I am a little weak on concepts, I fixed the number to be a million so that I could ask people to write shortest code to give out a specific output, but that shouldn't change the complexity of their algorithms for any other general case – Optimus – 2012-06-10T18:02:00.280
It is not specified but basis of log is still determinable, say in a binary search analysis determines that the base of log is 2 since the depth of a binary tree is log2(n) (and not ln(n) or log10n), but I do know, log2(n), ln(n) and other bases are obtainable multiplying by a common constant factor), so for this problem we'll just say O(logx(n))==O(log2(n))==O(log10(n)) which is the way it is normally assumed anyway – Optimus – 2012-06-10T19:00:27.857
@userunknown I think an md5sum would rarely be useful, there are many reasons that would cause the sum to be different for valid answers (one being windows \r\n vs linux \n, another being trailing spaces and endlines, encoding issues and many others) – Optimus – 2012-06-10T19:25:44.657
Google docs version keeps crashing my browser. Both Firefox and Chrome. Probably best to check out this version. http://primes.utm.edu/lists/small/millions/
– Kibbee – 2012-06-10T23:16:13.530@Optimus: If we have one line per prime, we surely have p\n and not \np, so there should be no problem with endlines. I don't see where spaces should occur from - they are out of spec. Encoding issues for decimal numbers? You're kidding! The only argument is MS-LFs, which can be clarified by 2 words like this: "\n EOLs" or healed with 2 md5sums. Another Idea would be a tail of the last 10, but this would simplify the job of finding the upper bound on calculation - depending on the way you do it. Instead of many words:
d21960bf14feb65190e5540c2996d0dfwith Unix EOLs. Last ends in...85863. – user unknown – 2012-06-10T23:55:11.1872Nobody seems to manage to calculates their complexity properly. There's confusion about whether
nis the number of primes or the maximum prime, and everyone ignores the fact that addition of numbers in the range0..nisO(logn), and multiplication and division are even more expensive. I suggest that you give some example algorithms along with their correct complexity. – ugoren – 2012-06-11T06:35:20.577I was thinking about that right now, should I change the problem statement to say 'find first n primes' instead of a million, That would make thing clearer in terms of complexity – Optimus – 2012-06-11T06:36:07.597
@ugoren I do plan to manage the scores and complexity myself, any help from anyone else is also welcome. I think after these edits, it should now be less ambiguous. – Optimus – 2012-06-11T07:15:03.960
3The current best known primality test for a k-bit number is
O-tilde(k^6). This leads to the implication that anyone who claims a running time better thanO-tilde(n ln n (ln(n ln n))^6)has misunderstood some part of the problem; and to the question as to howO-tildecomplexities should be handled in the scoring. – Peter Taylor – 2012-06-11T07:26:31.2032Nobody has pointed out, that O(n) is equivalent to O(kn) (for constant k) in complexity terms, but not in score terms. For example, suppose my complexity is O(n^10). That is equivalent to O(n^10 * 1E-308), and I may still win the challenge with a huge program with terrible complexity. – JDL – 2016-10-20T12:49:22.997
I am voting to close this challenge as "unclear what you're asking", the issue is pointed out by JDL above, and so far there has been an exploit attempt.
– user202729 – 2018-04-11T01:49:58.563