16
The Alternating Harmonic Series is a well known convergent series.
"Clearly", it is obvious that it converges to the natural log of 2. Or does it?
Since the series is not absolutely convergent, by simply rearranging the terms, I can make it approach anything I want. Suppose I want the series to converge to e. All I'd have to do is this:
If you didn't catch the pattern, there isn't an obvious one. Here's how it works:
- Consider the terms of the alternating harmonic series in terms of positive and negative terms.
- Add together just enough positive terms to exceed our target (e). (aka
sum > target) - Subtract the next negative term.
- Go back to 2.
Note that at step 2, if our sum == target, you should add another positive term.
From this we can define a sequence associated with each number as follows:
- Follow the algorithm above
- For each positive term, output 1.
- For each negative term, output 0.
Let's call this sequence the "Harmonious Bit Pattern" of a number. For example, the HBP of e begins as:
1, 1, 1, 1, <32 times>, 0, 1, 1, <54 times>, 0, 1, 1, ...
Your challenge:
You will be given:
- a rational input target in the range [-10, 10] (note: even reaching 10 via the harmonic series takes many millions of terms). This may be a decimal (aka
1.1) or you may take a rational directly (aka12/100) - a positive
intn input, specifying the number of terms of the Harmonious Bit Pattern to output.
You are expected to output the exact Harmonious Bit Pattern of the target to the specified number of terms. You may output space separated values, comma separated, no separation, etc; just as long as the pattern of 0s and 1s is clearly visible and is read left to right with consistent separation.
Test Cases
>>> 0, 1
1
>>> 0, 2
10
>>> 0, 7
1000010
>>> 1, 10
1101011011
>>> 1.01, 3
110
>>> 1.01, 24
110101101101101101101101
>>> 2.71, 32
11111111111111111111111111111111
>>> 2.71, 144
111111111111111111111111111111110111111111111111111111111111111111111111111111111111111101111111111111111111111111111111111111111111111111111111
>>> -9.8, 100
0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
Note that since -9.8 is so large, the first 1 that would be output is somewhere around the 149496620th term (that was computed via floats, so the value might not be exact).
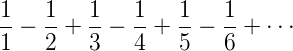
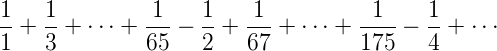
Defining
h a p qinstead ofh p q asaves a byte. – Zgarb – 2015-10-14T19:37:33.063Should be noted that 7 bytes are spent on just trimming the infinite result list to one of length n. It would actually be much nicer to just give the infinite list as the result. – ceased to turn counterclockwis – 2015-10-14T20:33:56.323