16
Given the number of vertices n ≥ 3 and the "step size" 1 ≤ m < n/2 (indicating the distance between two connected vertices), output a graphical representation of the corresponding regular polygram. If the polygram consist of multiple closed loops, each loop must be rendered in a different line colour. (If this sounds confusing, the examples below should hopefully clear things up.)
Rules
Any reasonable solution to the problem will likely satisfy these rules automatically - they are just there to put some constraints on the parameters of the output in order to prevent answers like "This black block is totally a polygram, but you can't see it because I set the line width to over 9000."
- You can render the polygram either to a file (which may be written to disc or to the standard output stream) or display it on the screen.
- You may use either vector or raster graphics. If your output is rasterised, your image must have dimensions of 400x400 pixels or more, and the polygram's radius (the distance from the centre to each vertex) must be between 35% and 50% of the side length.
- The aspect ratio of the polygram must be 1 (so that its vertices lie on a proper circle) - the canvas of the image may be rectangular.
- The lines of the polygram must be no thicker than 5% of the radius (and of course, they must have non-zero thickness to be visible).
- You may render axes or a frame in addition to the polygram, but nothing else.
- You may choose any (solid) background colour.
- For polygrams consisting of multiple closed loops, you must support at least 6 visually distinct colours, all of which must be different from the background. (Grey-scale is fine, provided the shades are sufficiently spread out through the spectrum.) Your code must still work for more than 6 loops, but the colours don't have to be distinguishable for any additional loops (i.e. you may also reuse colours from previous loops at that point).
This is code golf, so the shortest answer (in bytes) wins.
Examples
Here are all the outputs up to n = 16 (where the column corresponds to n and the row to m):
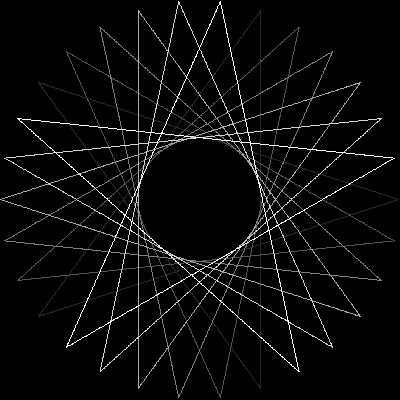
As examples for larger n, here are (n, m) = (29, 11) and (30, 12):

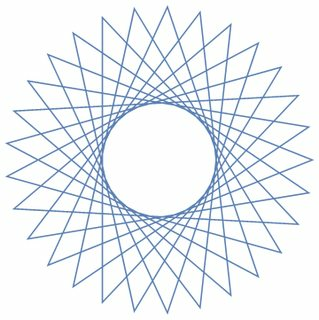
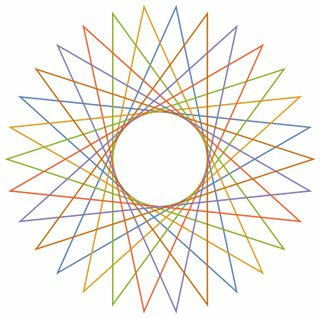
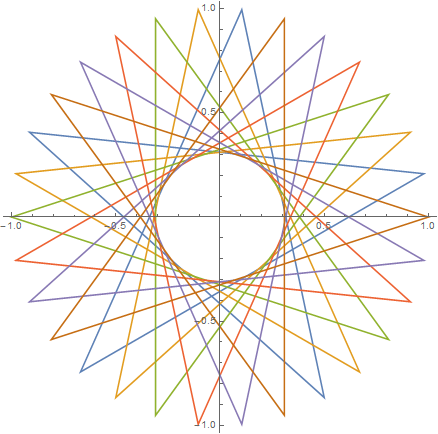
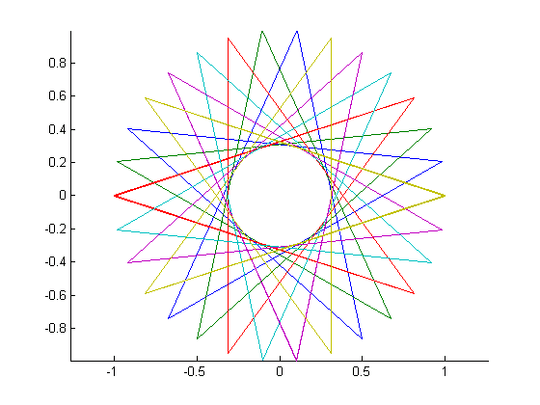
What about anti aliasing and stuff? (Since we are dealing with angled lines) – Optimizer – 2015-10-13T12:26:07.857
1@Optimizer I'm not going to prescribe an anti-aliasing algorithm. The lines may be aliased or anti-aliased as long as they are clearly visible. Use your best judgement. – Martin Ender – 2015-10-13T12:28:00.160