Draw the Devil's Staircase

Question

The Devil's Staircase is a fractal-like function related to the Cantor set.

Your task is to replicate this funky function — in ASCII art!

Input

A single integer n >= 0, indicating the size of the output. Input may be given via STDIN, function argument or command-line argument.

Output

The ASCII-art rendition of the Devil's staircase at size n, either returned as a string or printed to STDOUT. Trailing spaces at the end of each row are okay, but leading spaces are not. You may optionally print a single trailing newline.

For size 0, the output is just:

x

(If you wish, you may use any other printable ASCII character other than space, in place of x.)

For size n > 0, we:

• Take the output of size n-1 and stretch each row by a factor of three
• Riffle between rows of single xs
• Shift the rows rightward so that there is exactly one x in each column, and the position of the first x are minimal while decreasing with the rows

For example, the output for n = 1 is:

    x
 xxx
x

To get the output for n = 2, we stretch each row by a factor of three:

            xxx
   xxxxxxxxx
xxx

Riffle between rows of single x's:

x
            xxx
x
   xxxxxxxxx
x
xxx
x

Shift rightward:

                  x
               xxx
              x
     xxxxxxxxx
    x
 xxx
x

As another example, here is n = 3.

Scoring

This is code-golf, so the solution in the fewest bytes wins.

Answer 1

Pyth, 30

jb_u+G+*leGd*HNu+N+^3hTNUQ]1]k

This is a program that takes input from STDIN and uses grc's method of finding the Cantor set. Uses the " character to display the curve.

Try it online here.

Explanation:

I will explain the code in two parts, first, the cantor set generation:

u+N+^3hTNUQ]1
u        UQ]1         : reduce( ... , over range(input), starting with [1])
 +N                   : lambda N,T: N + ...
   +^3hTN             : 3 ** (T+1) + N   (int + list in pyth is interpreted as [int] + list)

And the output formatting:

jb_u+G+*leGd*HN    ]k
jb_                    : "\n".join(reversed(...)
   u               ]k  : reduce(lambda G,H: ... , over cantor set, starting with [""])
    +G+*leGd           : G + len(G[-1]) * " " + ...
            *HN        : H * '"'

Note that in pyth N = '"' by default.

Answer 2

J (73 68 58 41 39 38 35 34 characters)

After thinking about the problem for some time, I found an entirely different way to generate the Devil's Staircase pattern. The old answer including its explanation has been removed, you can look into the revisions of this answer to figure out how it was.

This answer returns an array of blanks and sharps, representing the devil's staircase.

' #'{~1(]|.@=@#~[:,3^q:)2}.@i.@^>:

Here is the answer split into its two parts in explicit notation:

f =: 3 : '|. = (, 3 ^ 1 q: y) # y'
g =: 3 : '(f }. i. 2 ^ >: y) { '' #'''

Explanation

The approach is a bit different, so observe and be amazed.

1. >: 3 – three incremented, that is,

   4
   

2. 2 ^ >: 3 – two to the power of three incremented, that is,

   16
   

3. i. 2 ^ >: 3 – the first 2 ^ >: 3 integers, that is,

   0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
   

4. }. i. 2 ^ 4 – the first 2 ^ >: 3 integers, beheaded, that is,

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
   

   Let's call this sequence s; we enter f now.

5. 1 q: s – the exponents of 2 in the prime decomposition of each item of s. In general, x q: y yields a table of the exponents for the first x primes in the prime decomposition of y. This yields:

   0
   1
   0
   2
   0
   1
   0
   3
   0
   1
   0
   2
   0
   1
   0
   

6. 3 ^ 1 q: s – three to the power of these exponents, that is,

    1
    3
    1
    9
    1
    3
    1
   27
    1
    3
    1
    9
    1
    3
    1
   

7. , 3 ^ 1 q: s – the ravel (that is, the argument with it's structure collapsed into a vector) of the previous result. This is needed because q: introduces an unwanted trailing axis. This yields

    1 3 1 9 1 3 1 27 1 3 1 9 1 3 1
   

8. (, 3 ^ 1 q: s) # s – each item of s replicated as often as the corresponding item in the previous result, that is,

   1 2 2 2 3 4 4 4 4 4 4 4 4 4 5 6 6 6 7 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 9 10 10 10 11 12 12 12 12 12 12 12 12 12 13 14 14 14 15
   

9. = (, 3 ^ 1 q: s) # s – the self classification of the previous result, this is, a matrix where each row represents one of the unique items of the argument, each column represents the corresponding item of the argument and each cell represents whether the items of row and column are equal, that is,

   1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 0 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 0
   0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
   

10. |. = (, 3 ^ 1 q: s) # s – the previous result flipped along the vertical axis.

11. (|. = (, 3 ^ 1 q: s) # s) { ' #' – the items of the previous result used as indices into the array ' #', so 0 is replaced by   and 1 is replaced by #, that is,

                                                                    #
                                                                 ### 
                                                                #    
                                                       #########     
                                                      #              
                                                   ###               
                                                  #                  
                       ###########################                   
                      #                                              
                   ###                                               
                  #                                                  
         #########                                                   
        #                                                            
     ###                                                             
    #      
    

    the result we want.

Answer 3

Hexagony, 217 bytes

This was immensely fun. Thank you for posting this challenge.

Full disclosure: The language (Hexagony) did not exist at the time this challenge was posted. However, I did not invent it, and the language was not designed for this challenge (or any other specific challenge).

){_2"_{\"{{""}"{'2//_.\><*\"\/_><[\]/3\'\_;|#__/(\2\'3_'}(#:|{$#{>_\//(#={/;01*&"\\_|[##={|}$_#></)]$_##|){*_.>.(/?#//~-="{}<_"=#/\}.>"%<.{#{x\"<#_/=&{./1#_#>__<_'\/"#|@_|/{=/'|\"".{/>}]#]>(_<\'{\&#|>=&{{(\=/\{*'"]<$_

Laid out hexagonally:

        ) { _ 2 " _ { \ "
       { { " " } " { ' 2 /
      / _ . \ > < * \ " \ /
     _ > < [ \ ] / 3 \ ' \ _
    ; | # _ _ / ( \ 2 \ ' 3 _
   ' } ( # : | { $ # { > _ \ /
  / ( # = { / ; 0 1 * & " \ \ _
 | [ # # = { | } $ _ # > < / ) ]
$ _ # # | ) { * _ . > . ( / ? # /
 / ~ - = " { } < _ " = # / \ } .
  > " % < . { # { x \ " < # _ /
   = & { . / 1 # _ # > _ _ < _
    ' \ / " # | @ _ | / { = /
     ' | \ " " . { / > } ] #
      ] > ( _ < \ ' { \ & #
       | > = & { { ( \ = /
        \ { * ' " ] < $ _

The program does not actually use the # instruction, so I used that character to show which cells are genuinely unused.

How does this program work? That depends. Do you want the short version, or the long?

Short explanation

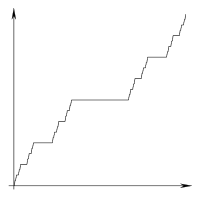
To illustrate what I mean by “line” and “segment” in the following explanation, consider this dissection of the intended output:

segments →
 │   │ │         │ │   │x   lines
─┼───┼─┼─────────┼─┼───┼─     ↓
 │   │ │         │ │xxx│
─┼───┼─┼─────────┼─┼───┘
 │   │ │         │x│
─┼───┼─┼─────────┼─┘
 │   │ │xxxxxxxxx│
─┼───┼─┼─────────┘
 │   │x│
─┼───┼─┘
 │xxx│
─┼───┘
x│

With that explained, the program corresponds to the following pseudocode:

n = get integer from stdin

# Calculate the number of lines we need to output.
line = pow(2, n+1)

while line > 0:
    line = line - 1

    # For all segments except the last, the character to use is spaces.
    ch = ' ' (space, ASCII 32)

    # The number of segments in each line is
    # equal to the line number, counting down.
    seg = line

    while seg > 0:
        seg = seg - 1

        # For the last segment, use x’s.
        if seg = 0:
            ch = 'x' (ASCII 120)

        # Calculate the actual segment number, where the leftmost is 1
        n = line - seg

        # Output the segment
        i = pow(3, number of times n can be divided by 2)
        i times: output ch

    output '\n' (newline, ASCII 10)

end program

Long explanation

Please refer to this color-coded code path diagram.

Execution starts in the top left corner. The sequence of instructions ){2'"''3''"2}?) is executed (plus a few redundant cancelations, like "{ etc.) by pursuing a fairly convoluted path. We start with Instruction Pointer #0, highlighted in crimson. Halfway through, we switch to #1, starting in the top-right corner and painted in forest green. When IP #2 starts out in cornflower blue (middle right), the memory layout is this:

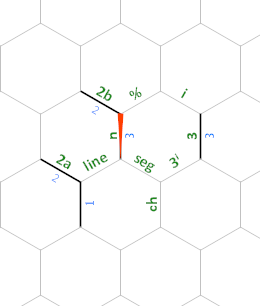
Throughout the entire program, the edges labeled 2a and 2b will always have the value 2 (we use them to calculate 2ⁿ⁺¹ and to divide by 2, respectively) and the edge labeled 3 will always be 3 (we use that to calculate 3ⁱ).

We get to business as we enter our first loop, highlighted in cornflower blue. This loop executes the instructions (}*{=&}{= to calculate the value 2ⁿ⁺¹. When the loop exits, the saddle brown path is taken, which takes us to Instruction Pointer #3. This IP merely dabbles along the bottom edge westwards in goldenrod yellow and soon passes control to IP #4.

The fuchsia path indicates how IP #4, starting in the bottom left, proceeds swiftly to decrement line, set ch to 32 (the space character) and seg to (the new value of) line. It is due to the early decrement that we actually start with 2ⁿ⁺¹−1 and eventually experience a last iteration with the value 0. We then enter the first nested loop.

We turn our attention to the branching indigo, where, after a brief decrement of seg, we see ch updated to x only if seg is now zero. Afterwards, n is set to line − seg to determine the actual number of the segment we’re in. Immediately we enter another loop, this time in the fair color of tomato.

Here, we figure out how many times n (the current segment number) can be divided by 2. For as long as the modulo gives us zero, we increment i and divide n by 2. When we are satisfied n is no longer thusly divisible, we branch into the slate gray, which contains two loops: first it raises 3 to the power of the i we calculated, and then it outputs ch that many times. Observe that the first of these loops contains a [ instruction, which switches control to IP #3 — the one that was only taking baby steps along the bottom edge earlier. The body of the loop (multiplying by 3 and decrementing) is executed by a lonely IP #3, imprisoned in an endless dark olive green cycle along the bottom edge of the code. Similarly, the second of these slate gray loops contains a ] instruction, which activates IP #5 to output ch and decrement, shown here in dark Indian red. In both cases, those Instruction Pointers trapped in servitude obediently execute one iteration at a time and yield control back to IP #4, only to bide the moment for their service to be called upon once again. The slate gray, meanwhile, rejoins its fuchsia and indigo brethren.

As seg inevitably reaches zero, the indigo loop exits into the lawn green path, which merely outputs the newline character and promptly merges back into the fuchsia to continue the line loop. Beyond the final iteration of the line loop lies the short sable ebon path of ultimate program termination.

Answer 4

Python 2, 78

L=[1]
i=3
exec"L+=[i]+L;i*=3;"*input()
while L:x=L.pop();print' '*sum(L)+'x'*x

Starting off with the list L=[1], we duplicate it and insert the next power of 3 in the middle, resulting in [1, 3, 1]. This is repeated n times to give us the row lengths for the Devil's staircase. Then we print each row padded with spaces.

Answer 5

APL, 38

⊖↑'x'/⍨¨D,⍨¨0,¯1↓-+\D←{1,⍨∊1,⍪3×⍵}⍣⎕,1

Example:

      ⊖↑'x'/⍨¨D,⍨¨0,¯1↓-+\D←{1,⍨∊1,⍪3×⍵}⍣⎕,1
⎕:
      2
                  x
               xxx 
              x    
     xxxxxxxxx     
    x              
 xxx               
x   

Explanation:

⊖↑'x'/⍨¨D,⍨¨0,¯1↓-+\D←{1,⍨∊1,⍪3×⍵}⍣⎕,1

                                     ⎕       ⍝ read a number from the keyboard
                       {           }⍣ ,1      ⍝ apply this function N times to [1]
                               3×⍵           ⍝ multiply each value by 3
                           ∊1,⍪               ⍝ add an 1 in front of each value
                        1,⍨                  ⍝ add an 1 to the end
                     D←                      ⍝ store values in D (lengths of rows)
                   +\                        ⍝ get running sum of D
                  -                          ⍝ negate (negative values on / give spaces)
             0,¯1↓                           ⍝ remove last item and add a 0 to the beginning
                                             ⍝ (each row needs offset of total length of preceding rows)   
         D,⍨¨                                ⍝ join each offset with each row length
   'x'/⍨¨                                    ⍝ get the right number of x-es and spaces for each row
 ↑                                           ⍝ make a matrix out of the rows
⊖                                            ⍝ mirror horizontally 

Answer 6

GNU sed, 142

Not the shortest answer, but its sed!:

s/$/:/
:l
s/x/xxx/g
s/:/:x:/g
tb
:b
s/^1//
tl
s/:x/X/g
s/^/:/
:m
s/.*:([Xx]+)Xx*:$/&\1:/
tm
:n
s/([ :])[Xx](x*Xx*)/\1 \2/g
tn
s/:/\n/g
s/X/x/g

Because this is sed (no native arithmetic), I'm taking liberties with the rule "A single integer n >= 0, indicating the size of the output". In this case the input integer must be a string of 1s, whose length is n. I think this is "indicating" the size of the output, even though it is not a direct numerical equivalent to n. Thus for n=2, the input string will be 11:

$ echo 11 | sed -rf devils-staircase.sed

                  x
               xxx
              x
     xxxxxxxxx
    x
 xxx
x

$ 

This appears to complete with exponential time complexity of O(cⁿ), where c is about 17. n=8 took about 45 minutes for me.

---

Alternatively if it is required that n is entered numerically exactly, then we can do this:

sed, 274 bytes

s/[0-9]/<&/g
s/9/8Z/g
s/8/7Z/g
s/7/6Z/g
s/6/5Z/g
s/5/4Z/g
s/4/3Z/g
s/3/2Z/g
s/2/1Z/g
s/1/Z/g
s/0//g
:t
s/Z</<ZZZZZZZZZZ/g
tt
s/<//g
s/$/:/
:l
s/x/xxx/g
s/:/:x:/g
tb
:b
s/^Z//
tl
s/:x/X/g
s/^/:/
:m
s/.*:([Xx]+)Xx*:$/&\1:/
tm
:n
s/([ :])[Xx](x*Xx*)/\1 \2/g
tn
s/:/\n/g
s/X/x/g

Output:

$ echo 2 | sed -rf devils-staircase.sed

                  x
               xxx
              x
     xxxxxxxxx
    x
 xxx
x

$ 

Answer 7

Python 2, 81

def f(n,i=1,s=0):
 if i<2<<n:q=3**len(bin(i&-i))/27;f(n,i+1,s+q);print' '*s+'x'*q

Program version (88)

def f(n,s=0):
 if n:q=3**len(bin(n&-n))/27;f(n-1,s+q);print' '*s+'x'*q
f((2<<input())-1)

The number of x's in the nth 1-indexed row is 3 to the power of (the index of the first set bit in n, starting from the lsb).

Answer 8

Python 2, 74

def f(n,s=0):
 if~n:B=3**n;A=s+B-2**n;f(n-1,A+B);print' '*A+'x'*B;f(n-1,s)

A recursive approach. The size-$n$ devil's staircase is split into three parts

• The left recursive branch, a staircase of size n-1, whose length is 3**n - 2**n
• The center line of x', of length 3**n
• The right recursive branch, a staircase of size n-1, whose length is 3**n - 2**n

Note that the total length of the three parts is 3*(3**n) - 2*(2**n) or 3**(n+1) - 2**(n+1), which confirms the induction.

The optional variable s stores the offset of the current parts we're printing. We first recurse down to the left branch with larger offset, then print the center line, then do the right branch at the current offset.

Answer 9

CJam, 36 35 33 bytes

Here is another CJam approach (I haven't looked at Optimizer's code, so I don't know if it's actually much different):

L0sl~{{3*0s}%0s\+}*{1$,S*\+}%W%N*

This uses 0 for the curve. Alternatively, (using grc's trick)

LLl~){3\#a1$++}/{1$,S*\'x*+}%W%N*

which uses x.

Test it here.

Explanation

The basic idea is to first form an array with the rows, like

["0" "000" "0" "000000000" "0" "000" "0"]

And then to go through this list, prepending the right amount of spaces.

L0sl~{{3*0s}%0s\+}*{1$,S*\+}%W%N*
L                                 "Push an empty string for later.";
 0s                               "Push the array containing '0. This is the base case.";
   l~                             "Read and evaluate input.";
     {           }*               "Repeat the block that many times.";
      {    }%                     "Map this block onto the array.";
       3*                         "Triple the current string.";
         0s                       "Push a new zero string.";
             0s\+                 "Prepend another zero string.";
                   {       }%     "Map this block onto the result.";
                    1$            "Copy the last line.";
                      ,S*         "Get its length and make a string with that many spaces.";
                         \+       "Prepend the spaces to the current row.";
                             W%   "Reverse the rows.";
                               N* "Join them with newlines.";

The other version works similarly, but creates an array of lengths, like

[1 3 1 9 1 3 1]

And then turns that into strings of xs in the final map.

Answer 10

Dyalog APL, 34 characters

Using the approach by grc. Draws the staircase with ⌹ (domino) characters and takes input from stdin. This solution assumes ⎕IO←0.

' ⌹'[(∪∘.=⊖){⍵/⍳≢⍵}⊃(⊢,,)/3*⌽⍳1+⎕]

• ⎕ – take input from stdin.
• ⌽⍳1+⎕ – the sequence of the numbers from ⎕ down to 0. (e.g. 3 2 1 0)
• 3*⌽⍳1+⎕ – three to the power of that (e.g. 27 9 3 1)
• (⊢,,)/3*⌽⍳1+⎕ – the previous result folded from the right by the tacit function ⊢,, which is equal to the dfn {⍵,⍺,⍵} yielding the step lengths of the devil's staircase as per grc's approach.
• {⍵/⍳≢⍵}⊃(⊢,,)/3*⌽⍳1+⎕ the step lengths converted into steps.
• (∪∘.=⊖){⍵/⍳≢⍵}⊃(⊢,,)/3*⌽⍳1+⎕ that self-classified, as in my J solution. Notice that ⊖ already flips the result correctly.
• ' ⌹'[(∪∘.=⊖){⍵/⍳≢⍵}⊃(⊢,,)/3*⌽⍳1+⎕] the numbers replaced by blanks and dominoes.

Answer 11

Ruby, 99

A different answer to my other one, inspired by FUZxxl's answer

FUZxxl notes that the numbers of x's correspond to the number of factors of 2 of the index. for example for n=2 we have the following factorization:

1 =1
2 =1 * 2
3 =3
4 =1 * 2 * 2
5 =5
6 =3 * 2
7 =7

I use a rather more straightforward way of extracting these powers of 2: i=m&-m which yields the sequence 1 2 1 4 1 2 1 etc. This works as follows:

m-1 is the same as min its most significant bits, but the least significant 1's bit becomes a zero, and all the zeros to the right become 1's.

To be able to AND this with the original, we need to flip the bits. There are various ways of doing this. One way is to subtract it from -1.

The overall formula is then m& (-1 -(m-1)) which simplifies to m&(-m)

Example:

          100   01100100
100-1=     99   01100011
-1-99=   -100   10011100
100&-100=   4   00000100

Here's the code: newlines are counted, indents are unnecessary and therefore not counted, as my other answer. It's slightly longer than my other answer due to the clumsy conversion from base 2: 1 2 1 4 1 2 1 etc to base 3: 1 3 1 9 1 3 1 etc (is there a way to avoid that Math:: ?)

def s(n)
  a=[]
  t=0
  1.upto(2*2**n-1){|m|i=3**Math::log(m&-m,2)
    a.unshift" "*t+"x"*i 
    t+=i}
  puts a
end

Answer 12

PHP - 137 bytes

function f($n){for($a=[];$i<=$n;array_push($a,3**$i++,...$a))$r=str_repeat;foreach($a as$v){$o=$r(' ',$s).$r(x,$v)."
$o";$s+=$v;}echo$o;}

I'm using here the same trick as grc. Here is the ungolfed version:

function staircase($n)
{
    $lengthsList = [];
    for ($i = 0; $i <= $n; ++$i) {
        array_push($lengthsList, 3 ** $i, ...$lengthsList);
    }

    $output = '';
    $cumulatedLength = 0;
    foreach ($lengthsList as $length)
    {
        $output = str_repeat(' ', $cumulatedLength) . str_repeat('x', $length) . "\n" . $output;
        $cumulatedLength += $length;
    }

    echo $output;
}

Answer 13

Ruby, 140 99

My second ever Ruby code, and my first nontrivial use of the language. Suggestions are most welcome. Byte count excludes leading spaces for indents, but includes newlines (it seems most of the newlines cannot be deleted unless they are replaced by a space at least.)

Input is by function call. Output is an array of strings, which ruby conveniently dumps to stdout as a newline-separated list with a single puts.

The algorithm is simply new iteration = previous iteration + extra row of n**3 x's + previous iteration. However there is a lot a fair amount of code just to get the leading spaces in the output right.

def s(n)
  a=["x"]
  1.upto(n){|m|t=" "*a[0].length
    a=a.map{|i|t+" "*3**m+i}+[t+"x"*3**m]+a}
  puts a
end

Edit: Ruby, 97

This uses the similar but different approach of building a numeric table of all the numbers of x's required in array a in the manner described above, but then building a table of strings afterwards. The table of strings is built backwards in array c using the rather oddly named unshift method to prepend to the existing array.

Currently this approach is looking better - but only by 2 bytes :-)

def s(n)
  a=c=[]
  (n+1).times{|m|a=a+[3**m]+a}
  t=0
  a.each{|i|c.unshift" "*t+"x"*i
    t+=i}
  puts c
end

Answer 14

Haskell, 99 characters

d=q.((iterate((1:).(>>=(:[1]).(*3)))[1])!!)
q[]=[];q(a:r)=sum r&' '++a&'x'++'\n':q r
(&)=replicate

The function is d:

λ: putStr $ d 3
                                                                x
                                                             xxx
                                                            x
                                                   xxxxxxxxx
                                                  x
                                               xxx
                                              x
                   xxxxxxxxxxxxxxxxxxxxxxxxxxx
                  x
               xxx
              x
     xxxxxxxxx
    x
 xxx
x

Answer 15

C, 165

#define W while
f(n){int i=n+1,j=1<<i,k=1,l,r,s,t;W(i--)k*=3;l=k-j;W(--j){r=j,s=1;W(!(r%2))r/=2,s*=3;l-=s;t=l;W(t--)putchar(32);W(++t<s)putchar(88);putchar('\n');}}

Here's the same code unpacked and slightly cleaned up:

int f(int n) {
    int i=n+1, j=1<<i, k=1;
    while (i--) k*=3;
    int l=k-j;
    while (--j) {
        int r=j,s=1;
        while (!(r%2))
            r/=2, s*=3;
        l-=s;
        int t=l;
        while (t--) putchar(' ');
        while (++t<s) putchar('X');
        putchar('\n');
    }
}

This is based on the same idea as FUZxxl's solution to the problem, of using an explicit rather than implicit form for the rows. The declaration of j sets it to 2^(n+1), and the first while loop computes k=3^(n+1); then l=3^(n+1)-2^(n+1) is the total width of the staircase (this isn't too difficult to prove). We then go through all the numbers r from 1 to 2^(n+1)-1; for each one, if it's divisible by (exactly) 2^n then we plan on printing s=3^n 'X's. l is adjusted to make sure we start from the right spot: we write l spaces and s 'X's, then a newline.

Answer 16

CJam, 46 43 41 39 36 35 bytes

L0ri),(a*+_W%(;+{3\#'x*+_,S*}%$1>N*

UPDATE using a different approach now.

---

Old approach:

]ri){3f*_,)"x"a*\]z:+}*_s,f{1$,U+:U-S*\N}

Pretty naive and long, but something to get started.

Will add explanation once I golf it.

Try it online here

Answer 17

Java, 271 269 bytes

Uses grc's method.

import java.util.*;String a(int a){List<Integer>b=new ArrayList<>();int c=-1,d=1;for(;c++<a;b.add(d),b.addAll(b),b.remove(b.size()-1),d*=3);String f="";for(;b.size()>0;f+="\n"){d=b.remove(b.size()-1);for(int g:b)for(c=0;c<g;c++)f+=' ';for(c=0;c<d;c++)f+='x';}return f;}

Indented:

import java.util.*;
String a(int a){
    List<Integer>b=new ArrayList<>();
    int c=-1,d=1;
    for(;c++<a;b.add(d),b.addAll(b),b.remove(b.size()-1),d*=3);
    String f="";
    for(;b.size()>0;f+="\n"){
        d=b.remove(b.size()-1);
        for(int g:b)
            for(c=0;c<g;c++)
                f+=' ';
        for(c=0;c<d;c++)
            f+='x';
    }
    return f;
}

Any suggestions are welcome.

2 bytes thanks to mbomb007

Answer 18

JavaScript (ES6) 104 106 118

Edit Removed the recursive function, the list of '*' for each line is obtained iteratively, fiddling with bits and powers of 3 (like in many other answers)
Inside the loop, a multiline string is buuilt from bottom up, keeping a running count of leading spaces to add on each line

F=n=>{
  for(i=a=s='';++i<2<<n;a=s+'*'.repeat(t)+'\n'+a,s+=' '.repeat(t))
    for(t=u=1;~i&u;u*=2)t*=3;
  return a
}

First Try removed

The recursive R function build an array with the number of '*' for each line. For instance R(2) is [1, 3, 1, 9, 1, 3, 1]
This array is scanned to build a multiline string from bottom up, keeping a running count of leading spaces to add on each line

F=n=>
(R=n=>[1].concat(...n?R(n-1).map(n=>[n*3,1]):[]))(n)
.map(n=>a=' '.repeat(s,s-=-n)+'*'.repeat(n)+'\n'+a,a=s='')
&&a 

Test In Firefox/FireBug console

F(3)

Output

                                                                *
                                                             ***
                                                            *
                                                   *********
                                                  *
                                               ***
                                              *
                   ***************************
                  *
               ***
              *
     *********
    *
 ***
*

Answer 19

Perl, 62

#!perl -p
eval's/x+/$&$&$&
x/g,s/\d*/x
/;'x++$_;s/x+/$"x$'=~y!x!!.$&/ge

First calculates the result iteratively without the leading spaces. Then adds them before each line according to the number of x characters in the rest of the string.

Answer 20

R - 111 characters

Straightforward implementation, building up the array iteratively and destroying it slowly.

n=scan()
a=1
if(n)for(x in 1:n)a=c(a,3^x,a)
for(A in a){cat(rep(' ',sum(a)-A),rep('x',A),'\n',sep='');a=a[-1]}

Usage:

> source('devil.r')
1: 2
2: 
Read 1 item
                  x
               xxx
              x
     xxxxxxxxx
    x
 xxx
x