C, 315 302 bytes
t,i;double o,w,h,x,y,k,a,b,c;double g(N,S)double N,S[][2];{for(t=0;t<N;t++)k+=S[t][1];k/=N;for(i=0;i<9;i++){o=w=h=0;for(t=0;t<N;t++)x=S[t][0],y=S[t][1],a=y-k,c=k*k-2*k*y+x*x+y*y,o+=-a/sqrt(x*x+a*a),w+=x*x/pow(c,1.5),h+=3*x*x*a/pow(c,2.5);a=h/2;b=w-h*k;c=o-w*k+a*k*k;k=(-b+sqrt(b*b-4*a*c))/h;}return k;}
This is far from pretty, and it's not short either. I figured since I'm not going to win the length contest, I can try to win the (theoretical) accuracy contest! The code is probably an order of magnitude or two faster than the bruteforce solution, and relies on a bit of mathematical tomfoolery.
We define a function g(N,S) which takes as input the number of houses, N, and an array of houses S[][2].
Here it is unraveled, with a test case:
t,i;
double o,w,h,x,y,k,a,b,c;
double g(N,S)double N,S[][2];{
/* Initially, let k hold the geometric mean of given y-values */
for(t=0;t<N;t++)
k+=S[t][1];
k/=N;
/* We approximate 9 times to ensure accuracy */
for(i=0;i<9;i++){
o=w=h=0;
for(t=0;t<N;t++)
/* Here, we are making running totals of partial derivatives */
/* o is the first, w the second, and h the third*/
x=S[t][0],
y=S[t][1],
a=y-k,
c=k*k-2*k*y+x*x+y*y,
o+=-a/sqrt(x*x+a*a),
w+=x*x/pow(c,1.5),
h+=3*x*x*a/pow(c,2.5);
/* We now use these derivatives to find a (hopefully) closer k */
a=h/2;
b=w-h*k;
c=o-w*k+a*k*k;
k=(-b+sqrt(b*b-4*a*c))/h;
}
return k;
}
/* Our testing code */
int main(int argc, char** argv) {
double test[2][2] = {
{5.7, 3.2},
{8.9, 8.1}
};
printf("%.20lf\n", g(2, test));
return 0;
}
Which outputs:
5.11301369863013732697
Warning: Knowledge of some calculus may be required for a complete understanding!
So, let's talk about the math.
We know the distance from our desired point (0, k) and a house i:
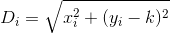
And thus the total distance D from n houses can be defined as follows:
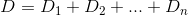
What we would like to do is minimize this function by taking a derivative with respect to k and setting it equal to 0. Let's try it. We know that the derivatives of D can be described as follows:
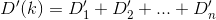
But the first partial derivative of each Di is pretty bad...
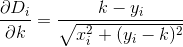
Unfortunately, even with n == 2, setting these derivatives to 0 and solving for k becomes disastrous very quickly. We need a more robust method, even if it requires some approximation.
Enter Taylor Polynomials.
If we know the value of D(k0) as well as all of D's derivatives at k0, we can rewrite D as a Taylor Series:
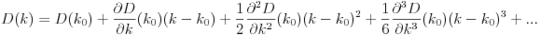
Now, this formula's got a bunch of stuff in it, and its derivatives can get pretty unwieldy, but we now have a polynomial approximation of D!
Doing a little bit of calculus, we find the next two derivatives of D by evaluating the derivatives of Di, just as before:
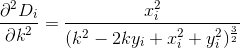
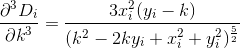
By truncation and evaluating the derivatives, we may now approximate D as a 3rd degree polynomial of the form:
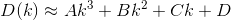
Where A, B, C, D are simply real numbers.
Now this we can minimize. When we take a derivative and set it equal to 0, we will end up with an equation of the form:
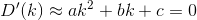
Doing the calculus and substitutions, we come up with these formulas for a, b, and c:
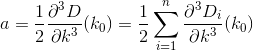
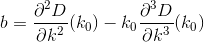
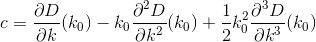
Now our problem gives us 2 solutions given by the quadratic formula:
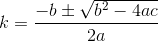
The entire formula for k would be a massive burden to write out, so we do it in pieces here and in the code.
Since we know that the higher k will always result in the minimum distance of our approximate D (I have a truly marvelous proof of this, which the margin of this paper is insufficient to contain...) we do not even have to consider the smaller of the solutions.
One final problem remains. For accuracy purposes, it is necessary that we begin with a k0 that is at least in the ballpark of where we expect the answer to be. For this purpose, my code chooses the geometric mean of the y-values of every house.
As a fail-safe, we repeat the entire problem again 9 times, replacing k0 with k at every iteration, to ensure accuracy.
I haven't done the math about how many iterations and how many derivatives are truly necessary, but I've opted to err on the side of caution until I can confirm accuracy.
If you made it through that with me, thank you so much! I hope you understood, and if you spot any mistakes (of which there are likely many, I'm very tired), please let me know!
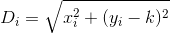
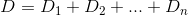
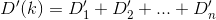
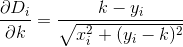
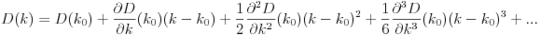
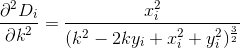
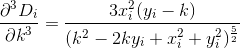
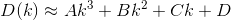
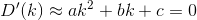
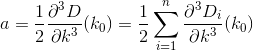
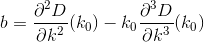
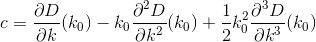
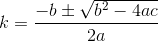
What metric is used for the distance function
D? Euclidean? – Reto Koradi – 2015-05-28T20:55:13.1671Even though there is only one main road, do we assume that a customer travels in a straight line from their house to the restaurant? Or do they travel directly to the y axis first? (Or in other words, do we use Euclidean or Manhattan distance for D?) – trichoplax – 2015-05-28T20:59:09.747
1(This can be worked out from the example but it would be nice to have it stated explicitly.) – trichoplax – 2015-05-28T21:01:32.447
@trichoplax Euclidean? Does Euclidean mean
sqrt(diffX^2 + diffY^2)? Then Euclidean. I know it doesn't fit the scenario perfectly but assume that the customer travels in a straight line somehow from his/her house. – soktinpk – 2015-05-28T21:59:22.710Can the input be taken in our language's preferred form from STDIN? – isaacg – 2015-05-28T23:18:16.017
@isaacg sure but as long as you don't do anything absurd as in "for my program, the input should also include the output or the program won't work" – soktinpk – 2015-05-28T23:20:45.250
5Is taking input as a list of complex numbers representing houses' positions on the complex plane acceptable? – lirtosiast – 2015-05-28T23:46:21.677
@ThomasKwa I think that's fine – soktinpk – 2015-05-29T01:03:44.097