56
9
In this challenge, the goal is to recreate the On-Line Encyclopedia of Integer Sequences one sequence at a time. Similar to the Evolution of Hello World, each answer depends on a previous answer.
Over time, this challenge will create a "family tree" of the OEIS sequences. It is simple to add on to this tree.
- Find a previous answer, which can be at any depth N of the tree.
- Determine the first N numbers generated by that answer's sequence.
- Find a sequence in OEIS which starts with those same numbers and which hasn't been used before.
- Write a program to generate this new sequence you just found.
- Submit your answer as depth N+1
Since the level of your answer influences scoring, you should always add your answer onto the tree at the deepest level possible. If you cannot fit your answer anywhere on the tree, you can start a new branch of the tree and put your answer as depth 1.
Answer Requirements
There are a few ways to output a sequence.
The first option is to write a program or function that inputs a number (from STDIN or as an argument) and returns the Nth number in your chosen sequence. You can assume that the sequence will be defined for N and that N and S_N are "reasonably sized" (so it won't cause overflows). You can also use any reasonable indexing, such as 0 indexing, 1 indexing, or the indexing listed under "offset" on the sequence's OEIS page, that doesn't matter. The term produced by the first index must match the first term of the OEIS entry.
The second option is to write a program or function that inputs a number and returns the first N terms of the sequence. The first terms of the output must be the first terms of the OEIS entry (you can't leave off the first few terms). Consecutive terms must be delimited by arbitrary strings of non-digit characters, so 0,1 1.2/3,5;8,11 works but 011235811 does not count.
The third option is to create a program that outputs a continuous stream of numbers. Similarly to the second option, there must be delimiters between consecutive terms.
Your answer should contain a header like this to aid Stack Snippet parsing:
# [language], [number] bytes, depth [number], A[new sequence] from A[old sequence]
Your answer should contain the code to generate the sequence, along with the first few terms that any descendants will need to contain. These few terms should be preceded by the exact word terms: so that the controller can use them as part of the tree diagram. It is also recommended to write a description of the sequence you chose.
If your post is a depth 1 answer and thus has no ancestor, you should simply omit the from A[number] in your header.
Here is an example answer:
# Perl, 26 bytes, depth 3, A026305 from A084912
various code here
and here
The next answer should match the following terms:
1, 4, 20
This sequence is .... and does ....
Chaining Requirements
In order to make this challenge more fair, there are restrictions on which answers you can chain yours to. These rules are mostly to prevent a single person from creating a whole branch of the tree by themselves or owning a lot of "root" nodes.
- You cannot chain to yourself.
- You cannot directly chain two of your answers to the same ancestor.
- You cannot make more than one "Level 1" answer.
Also, if the ancestor was of depth N, your post must have depth N+1, even if more than the required number of terms agree.
Scoring
Your score as a user is the sum of the scores of all of your answers. The score of a single answer is determined by the following formula:
Answer Score = Sqrt(Depth) * 1024 / (Length + 256)
This scoring system should encourage users to submit a large number of deeper answers. Shorter answers are preferred over longer answers, but depth has a much larger influence.
Below is a stack snippet that generates a leaderboard as well as a tree diagram of all of the answers. I would like to thank Martin Büttner and d3noob as the sources for a lot of this code. You should click "Full screen" to see the complete results.
function answersUrl(t){return"https://api.stackexchange.com/2.2/questions/"+QUESTION_ID+"/answers?page="+t+"&pagesize=100&order=desc&sort=creation&site=codegolf&filter="+ANSWER_FILTER}function getAnswers(){jQuery.ajax({url:answersUrl(page++),method:"get",dataType:"jsonp",crossDomain:!0,success:function(t){answers.push.apply(answers,t.items),t.has_more?getAnswers():process()}})}function shouldHaveHeading(t){var e=!1,r=t.body_markdown.split("\n");try{e|=/^#/.test(t.body_markdown),e|=["-","="].indexOf(r[1][0])>-1,e&=LANGUAGE_REG.test(t.body_markdown)}catch(a){}return e}function shouldHaveScore(t){var e=!1;try{e|=SIZE_REG.test(t.body_markdown.split("\n")[0])}catch(r){}return e}function getAuthorName(t){return t.owner.display_name}function decodeEntities(t){return $("<textarea>").html(t).text()}function process(){answers=answers.filter(shouldHaveScore).filter(shouldHaveHeading),answers.reverse();var t={},e=[],r=1,a=null,n=1,s=[];answers.forEach(function(t){var r=t.body_markdown.split("\n")[0],a=getAuthorName(t),n=r.match(SEQUENCE_REG)[0];n=n.trim();var o="from A000000";PARENT_REG.test(r)&&(o=r.match(PARENT_REG)[0]),o=o.substring(5).trim(),"A000000"==o&&(o="OEIS");var i="";SEQDATA_REG.test(t.body_markdown)&&(i=t.body_markdown.match(SEQDATA_REG)[1]);for(var u=!0,c=0;c<e.length;++c)u=u&&!(e[c]===n);for(var l=!0,c=0;c<e.length;++c)l=!(!l||e[c]===n||e[c]===n+a||e[c]===o+a);e.push(n),e.push(n+a),e.push(o+a),u&&data.push({name:n,parent:o,term:i+" : ",author:decodeEntities(a),URL:t.share_link}),l&&s.push(t)}),answers.sort(function(t,e){var r=t.body_markdown.split("\n")[0].match(SEQUENCE_REG),a=e.body_markdown.split("\n")[0].match(SEQUENCE_REG);return a>r?-1:r>a?1:void 0}),answers.forEach(function(e){var o=e.body_markdown.split("\n")[0],i=(o.match(NUMBER_REG)[0],(o.match(SIZE_REG)||[0])[0]),u=parseInt((o.match(DEPTH_REG)||[0])[0]).toString(),c=o.match(SEQUENCE_REG)[0],l="from A000000";PARENT_REG.test(o)&&(l=o.match(PARENT_REG)[0]),l=l.substring(5);var d=o.match(LANGUAGE_REG)[1];d.indexOf("]")>0&&(d=d.substring(1,d.indexOf("]")));for(var p=getAuthorName(e),E=!1,h=0;h<s.length;++h)E=E||s[h]===e;if(E){var f=jQuery("#answer-template").html();i!=a&&(n=r),a=i,++r;var m=1024*Math.pow(parseInt(u),.5)/(parseInt(i)+256);f=f.replace("{{SEQUENCE}}",c).replace("{{SEQUENCE}}",c).replace("{{NAME}}",p).replace("{{LANGUAGE}}",d).replace("{{SIZE}}",i).replace("{{DEPTH}}",u).replace("{{LINK}}",e.share_link),f=jQuery(f),jQuery("#answers").append(f),t[p]=t[p]||{lang:d,user:p,size:"0",numanswers:"0",link:e.share_link},t[p].size=(parseFloat(t[p].size)+m).toString(),t[p].numanswers=(parseInt(t[p].numanswers)+1).toString()}});var o=[];for(var i in t)t.hasOwnProperty(i)&&o.push(t[i]);o.sort(function(t,e){return parseFloat(t.size)>parseFloat(e.size)?-1:parseFloat(t.size)<parseFloat(e.size)?1:0});for(var u=0;u<o.length;++u){var c=jQuery("#language-template").html(),i=o[u];c=c.replace("{{RANK}}",u+1+".").replace("{{NAME}}",i.user).replace("{{NUMANSWERS}}",i.numanswers).replace("{{SIZE}}",i.size),c=jQuery(c),jQuery("#languages").append(c)}createTree()}function createTree(){function t(){var t=i.nodes(root).reverse(),e=i.links(t);t.forEach(function(t){t.y=180*t.depth});var r=c.selectAll("g.node").data(t,function(t){return t.id||(t.id=++o)}),a=r.enter().append("g").attr("class","node").attr("transform",function(t){return"translate("+t.y+","+t.x+")"});a.append("a").attr("xlink:href",function(t){return t.URL}).append("circle").attr("r",10).style("fill","#fff"),a.append("text").attr("x",function(){return 0}).attr("y",function(){return 20}).attr("dy",".35em").attr("text-anchor",function(){return"middle"}).text(function(t){return t.term+t.name}).style("fill-opacity",1),a.append("text").attr("x",function(){return 0}).attr("y",function(){return 35}).attr("dy",".35em").attr("text-anchor",function(){return"middle"}).text(function(t){return t.author}).style("fill-opacity",1);var n=c.selectAll("path.link").data(e,function(t){return t.target.id});n.enter().insert("path","g").attr("class","link").attr("d",u)}var e=data.reduce(function(t,e){return t[e.name]=e,t},{}),r=[];data.forEach(function(t){var a=e[t.parent];a?(a.children||(a.children=[])).push(t):r.push(t)});var a={top:20,right:120,bottom:20,left:120},n=3203-a.right-a.left,s=4003-a.top-a.bottom,o=0,i=d3.layout.tree().size([s,n]),u=d3.svg.diagonal().projection(function(t){return[t.y,t.x]}),c=d3.select("body").append("svg").attr("width",n+a.right+a.left).attr("height",s+a.top+a.bottom).append("g").attr("transform","translate("+a.left+","+a.top+")");root=r[0],t(root)}var QUESTION_ID=49223,ANSWER_FILTER="!t)IWYnsLAZle2tQ3KqrVveCRJfxcRLe",data=[{name:"OEIS",parent:"null",term:"",author:"",URL:"https://oeis.org/"}],answers=[],page=1;getAnswers();var SIZE_REG=/\d+(?=[^\d&]*(?:<(?:s>[^&]*<\/s>|[^&]+>)[^\d&]*)*,)/,DEPTH_REG=/\d+, A/,NUMBER_REG=/\d+/,LANGUAGE_REG=/^#*\s*([^,]+)/,SEQUENCE_REG=/A\d+/,PARENT_REG=/from\s*A\d+/,SEQDATA_REG=/terms:\s*(?:(?:-)?\d+,\s*)*((?:-)?\d+)/;body{text-align: left !important}#answer-list{padding: 10px; width: 550px; float: left;}#language-list{padding: 10px; width: 290px; float: left;}table thead{font-weight: bold;}table td{padding: 5px;}.node circle{fill: #fff; stroke: steelblue; stroke-width: 3px;}.node text{font: 12px sans-serif;}.link{fill: none; stroke: #ccc; stroke-width: 2px;}<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script><script src="http://d3js.org/d3.v3.min.js"></script><link rel="stylesheet" type="text/css" href="//cdn.sstatic.net/codegolf/all.css?v=83c949450c8b"><div id="answer-list"> <h2>Sequence List</h2> <table class="answer-list"> <thead> <tr> <td>Sequence</td><td>Author</td><td>Language</td><td>Size</td><td>Depth</td></tr></thead> <tbody id="answers"></tbody> </table></div><div id="language-list"> <h2>Leaderboard</h2> <table class="language-list"> <thead> <tr> <td>Rank</td><td>User</td><td>Answers</td><td>Score</td></tr></thead> <tbody id="languages"></tbody> </table></div><table style="display: none"> <tbody id="answer-template"> <tr> <td><a href="https://oeis.org/{{SEQUENCE}}">{{SEQUENCE}}</a></td><td>{{NAME}}</td><td>{{LANGUAGE}}</td><td>{{SIZE}}</td><td>{{DEPTH}}</td><td><a href="{{LINK}}">Link</a> </td></tr></tbody></table><table style="display: none"> <tbody id="language-template"> <tr> <td>{{RANK}}</td><td>{{NAME}}</td><td>{{NUMANSWERS}}</td><td>{{SIZE}}</td></tr></tbody></table>


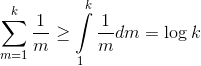
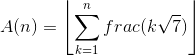
This page might help if you're looking for specific types of sequences, e.g. easy-to-compute ones. – Sp3000 – 2015-04-26T17:23:58.783
5You know, I think this is might just be the single coolest codegolf.sx question I've ever seen asked. It's not just cool, but actually useful as an archive. – Todd Lehman – 2015-04-26T19:08:45.653
3Given the OEIS is online, takes N terms of a sequence as a search term, and contains mathematica or maple code for many of the sequences, it would be possible to write a meta-entry which searched for the best scoring entry for which code exists in OEIS which is a descendent of any given entry here and posted it. – abligh – 2015-04-26T19:10:53.643
2Can I recommend some way of marking on the graph the snippet generates that a node is terminal, ie there are no unused sequences of a greater depth available on the OEIS? – Claudiu – 2015-04-27T05:52:52.820
1I think the only way to keep this challenge going would be to provide something where you give your username, and it lists the OEIS problems you could do, in order from highest depth to lowest. Otherwise it takes too long to find the next sequence to post. – Claudiu – 2015-05-04T22:38:06.987
Any score penalty for using a language created after this challenge? Is the answer simply non competing? – Luis Mendo – 2016-02-01T17:25:02.860
Can you use a sequence created after this challenge? – LegionMammal978 – 2016-03-09T21:34:12.263
What are the numbers on each node in the snippet's tree?
[thisNum?] : A[seq]– mbomb007 – 2016-03-09T21:47:09.313@mbomb007 The left number is the term added to the tree by that particular answer. For example, if you start at the root and follow the path
1:->2:->4:then every "child" sequence of the4:node starts with1 2 4. – PhiNotPi – 2016-03-09T21:57:43.020@PhiNotPi In that case, shouldn't this answer be depth two, because there's already a level 1 node starting with a
– mbomb007 – 2016-03-09T21:59:38.1401?you should always add your answer onto the tree at the deepest level possible. – mbomb007 – 2016-03-09T22:27:04.907
In this challenge, your goal is to recreate all of Wikipedia – phase – 2016-03-19T13:57:18.737
What's the OEIS for
0,1,1,2,3,5,8,11Base 12 Fibonacci? – CalculatorFeline – 2016-04-08T01:08:20.1571The SVG is slightly too narrow. – CalculatorFeline – 2016-04-08T01:17:07.593